JEE Main Important Formulas 2026 for Physics, Chemistry, Maths

JEE Main Formulas 2026 for Physics, Chemistry, Maths

Candidates must make a handy note of all important formulas to revise frequently. Candidates must have a good command of each topic and the formulas to crack the JEE Main 2026 exam to ace the test. Through this article, students can find the provided JEE Main formulas for all three subjects. Knowing important formulas in depth can help you solve problems fast and accurately, which is important for scoring well in JEE Main. All the formulas given here are according to the JEE Main 2026 syllabus strictly. JEE all formulas pdf subject wise are given below.

JEE Main 2026 Exam Pattern

The exam is divided into two main sections:

Section A: The quizzes contained in this section are 20 MCQs for each course. What the MCQ requires is four options and only one of them is the right answer.

Section B: This section has 5 numerical value questions for each of the subject areas, and the candidate only has to answer all five of these. These numerical value questions have to be answered accurately, sometimes to the second decimal place.

JEE Main Formulas for Physics 2026

Aspirants preparing for JEE Mains must remember that along with concepts one needs to revise and remember the formulas, which are very important while solving any problems. As JEE Main Physics formulas are given below, these formulas need to be memorized daily as direct questions and formulas are asked in exams. Students can also solve JEE Main Chapter Wise PYQs.

Physics and Measurement

1. Relative density $=\frac{\text { density of object }}{\text { density of water at } 4^{\circ} \mathrm{c}}$
2. Absolute Error for $\mathrm{n}^{\text {th }}$ reading $=\Delta a_n=a_m-a_n=$ true value - measured value

3. Mean absolute error

   $\Delta \bar{a}=\frac{\left|\Delta a_1\right|+\left|\Delta a_2\right|+\ldots\left|\Delta a_n\right|}{n}$

4. $\begin{aligned} & \text { Relative error }=\frac{\Delta \bar{a}}{a_m} \\ & \Delta \bar{a}=\text { mean absolute error } \\ & a_m=\text { mean value }\end{aligned}$

5. Percentage error $=\frac{\Delta \bar{a}}{a_m} \times 100 \%$

Kinematics

1. Some important Formulas of differentiation

   $\begin{aligned}
   & \frac{d}{d x}\left(x^n\right)=n x^{n-1} \\
   & \frac{d}{d x} \sin x=\cos x \\
   & \frac{d}{d x} \cos x=-\sin x \\
   & \frac{d}{d x} \tan x=\sec ^2 x \\
   & \frac{d}{d x} \cot x=-\csc ^2 x \\
   & \frac{d}{d x} \sec x=\sec x \tan x \\
   & \frac{d}{d x} \csc x=-\csc x \cot x \\
   & \frac{d}{d x} e^x=e^x \\
   & \frac{d}{d x} a^x=a^x \ln a \\
   & \frac{d}{d x} \ln |x|=\frac{1}{x}
   \end{aligned}$

2. Some important Formulas of integration

   $\begin{aligned}
   & \int x^n d x=\frac{x^{n+1}}{n+1}+C \\
   & \int \frac{d x}{x}=\ln |x|+C \\
   & \int e^x d x=e^x+C \\
   & \int a^x d x=\frac{1}{\ln a} a^x+C \\
   & \int \ln x d x=x \ln x-x+C \\
   & \int \sin x d x=-\cos x+C \\
   & \int \cos x d x=\sin x+C \\
   & \int \tan x d x=-\ln |\cos x|+C \\
   & \int \cot x d x=\ln |\sin x|+C \\
   & \int \sec x d x=\ln |\sec x+\tan x|+C \\
   & \int \csc x d x=-\ln |\csc x+\cot x|+C \\
   & \int \sec 2 x d x=\tan x+C \\
   & \int \csc c^2 x d x=-\cot x+C \\
   & \int \sec x \tan x d x=\sec x+C \\
   & \int \csc x \cot x d x=-\csc x+C \\
   & \int \frac{d x}{\sqrt{a^2-x^2}}=\sin ^{-1} \frac{x}{a}+C \\
   & \int \frac{d x}{a^2+x^2}=\frac{1}{a} \tan ^{-1} \frac{x}{a}+C \\
   & \int \frac{d x}{x \sqrt{x^2-a^2}}=\frac{1}{a} \sec ^{-1} \frac{|x|}{a}+C
   \end{aligned}$

3. $\vec{A} \times \vec{B}=A B \sin \theta$

4. $\begin{aligned} \text { Speed } & =\frac{\text { Change in distance }}{\text { change in time }} \\ v & =\frac{\text { distance }}{\text { time }}\end{aligned}$
5. Average speed $=\frac{\text { total distance covered }}{\text { total time taken }}$
6. $\begin{aligned} & \text { Average Velocity }=\frac{\text { Total Displacement }}{\text { Total time taken }}, \\ & \vec{V}_{\text {avg }}=\frac{\vec{S}_{\text {net }}}{t}\end{aligned}$
7. $\vec{a}=\frac{\text { change in velocity }}{\text { time taken }}=\frac{\vec{v}_f-\vec{v}_i}{t}$
8. $v=u+a t$
9. $s=u t+\frac{1}{2} a t^2$
10. $v^2-u^2=2 a s$

11. Average angular velocity-

    $\omega_{a v g}=\frac{\Delta \theta}{\Delta t}$

12. Time of flight

    $T=\frac{2 U \sin \theta}{g \cos \beta}$

13. Range along incline plane

    $R=\frac{2 u^2 \cdot \sin (\alpha-\beta) \cdot \cos \alpha}{g \cos ^2 \beta}$

Laws of motion

1. Inertial mass $(k g)=\frac{F}{a}$
2. Recoiling of Gun $\begin{aligned} & F=V_{\text {rel }}\left(\frac{d m}{d t}\right)=V(\mathrm{mn}) \\ & F=m n v \\ & F=\text { force required to hold the gun } \\ & n=\text { no.of bullets }\end{aligned}$
3. Force in non-uniform Circular Motion: $\begin{aligned} & F_c=m a_c=\frac{m v^2}{r} \quad\left(\vec{F}_c \perp \vec{v}\right) \\ & \mathrm{F}_{\mathrm{t}}=\mathrm{ma}_{\mathrm{t}} \\ & F_{\text {net }}=m \sqrt{a_c^2+a_t^2} \\ & \mathrm{~m}=\text { mass } \\ & \mathrm{a}_{\mathrm{c}}=\text { centripetal acceleration } \\ & \mathrm{a}_{\mathrm{t}}=\text { tangential acceleration } \\ & \mathrm{F}_{\mathrm{c}}=\text { centripetal force }\end{aligned}$

Work Energy and Power

1. Work $=$ force $\times$ displacement $\times \cos \theta$
2. Kinetic Energy $=0.5 \times m \times v^2$
3. Potential Energy $=m \times g \times h$
4. Law of conservation of Energy $\Delta K+\Delta U=\Delta E=W_{f n c}$

5. Average power-

   $P_{a v}=\frac{\Delta w}{\Delta t}=\frac{\int_0^t p \cdot d t}{\int_0^t d t}$

6. Instantaneous power-

   $P=\frac{d w}{d t}=P=\vec{F} \cdot \vec{v}$
   Where, $\vec{F} \rightarrow$ force

   $\vec{v} \rightarrow \text { velocity }$

7. In Perfectly Inelastic Collision:

   When the colliding bodies are moving in the same direction

   $\begin{aligned}
   & m_1 u_1+m_2 u_2=\left(m_1+m_2\right) v \\
   & v=\frac{m_1 u_1+m_2 u_2}{\left(m_1+m_2\right)}
   \end{aligned}$

   Loss in kinetic energy

   $\begin{aligned}
   & \Delta K \cdot E=\left(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2\right)-\left(\frac{1}{2}\left(m_1+m_2\right) V^2\right) \\
   & \Delta K \cdot E=\frac{1}{2}\left(\frac{m_1 m_2}{m_1+m_2}\right)\left(u_1-u_2\right)^2
   \end{aligned}$

   
   When the colliding bodies are moving in the opposite direction
   $\begin{aligned}
   & m_1 u_1+m_2\left(-u_2\right)=\left(m_1+m_2\right) v \\
   & v=\frac{m_1 u_1-m_2 u_2}{m_1+m_2}
   \end{aligned}$

   Loss in kinetic energy

   $\begin{aligned}
   & \Delta K \cdot E=\left(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2\right)-\left(\frac{1}{2}\left(m_1+m_2\right) V^2\right) \\
   & \Delta K \cdot E=\frac{1}{2}\left(\frac{m_1 m_2}{m_1+m_2}\right)\left(u_1+u_2\right)^2
   \end{aligned}$

8. Center of mass:

   For a system of N discrete particles

   $\begin{aligned}
   x_{c m} & =\frac{m_1 x_1+m_2 x_2 \ldots \ldots \ldots}{m_1+m_2 \ldots \ldots} \\
   y_{c m} & =\frac{m_1 y_1+m_2 y_2+m_3 y_3 \ldots \ldots \ldots}{m_1+m_2+m_3 \ldots \ldots} \\
   z_{c m} & =\frac{m_1 z_1+m_2 z_2+m_3 z_3 \ldots \ldots \ldots}{m_1+m_2+m_3 \ldots \ldots}
   \end{aligned}$

9. Velocity of the centre of mass

   $\vec{v}_{C M}=\frac{m_1 \vec{v}_1+m_2 \vec{v}_2 \ldots \ldots \ldots}{m_1+m_2 \ldots \ldots \ldots}$

10. Acceleration of centre of mass

    $\vec{a}_{C M}=\frac{m_1 \vec{a}_1+m_2 \vec{a}_2 \ldots \ldots \ldots}{m_1+m_2 \ldots \ldots .}$

11. Moment of inertia of a particle

    $I=m r^2$

12. Radius of gyration (K): $K=\sqrt{\frac{I}{M}}$

Gravitation

1. Gravitational force $\vec{F}=G\left[\frac{M m}{r^2}\right]^r$
2. Acceleration due to gravity $g=\frac{G M}{R^2}$
3. Gravitational field Intensity:

   $\vec{I}=\frac{\vec{F}}{m}$

   $\vec{I} \rightarrow G$. field Intensity
   $m \rightarrow$ mass of object
   $\vec{f} \rightarrow$ Gravitational Force

4. Gravitational Potential: $\begin{aligned} & V=-\int \vec{I} \cdot \overrightarrow{d r} \\ & V \rightarrow \text { Gravitational potential } \\ & I \rightarrow \text { Field Intensity } \\ & d r \rightarrow \text { small distance }\end{aligned}$

Mechanical Properties of Solids

1. The magnitude of stress, $\sigma=\frac{F}{A}$
   Unit of stress: $N / m^2$ or Pascal(Pa)
   Dimension of stress: $\left[M L^{-1} T^{-2}\right]$
2. Volume stress $=\frac{F}{A}=P$
3. Longitudinal strain $=\frac{\Delta L}{L}$
4. Hooke’s law:" $\begin{gathered}\text { Stress } \alpha \text { Strain } \\ \Rightarrow \text { Stress }=E(\text { Strain }) \\ \Rightarrow E=\frac{\text { Stress }}{\text { Strain }}\end{gathered}$
5. Young's Modulus(Y): $Y=\frac{\text { longitudinal stress }}{\text { longitudinal strain }}=\frac{F / A}{\Delta L / L}=\frac{F l}{A \Delta L}$
6. Modulus of rigidity(G): $G=\frac{\text { shearing stress }}{\text { shearing strain }}=\frac{F / A}{x / L}=\frac{F l}{A x}=\frac{F}{A \phi}$
7. Bulk Modulus(B):

   $\begin{gathered}
   \text { Volumestress }=\frac{F}{A}=\text { Pressure } \\
   \qquad B=-\frac{P}{\Delta V / V}
   \end{gathered}$

   where $\mathrm{P}=$ increase in pressure, $\mathrm{V}=$ original volume, $\Delta V=$ change in volume

Mechanical Properties of Fluids

1. Pressure $P=\frac{F}{A}$
2. Buoyant force $F_B=\rho V g$

   Where $\mathrm{F}_{\mathrm{B}}=$ Buoyant force

   $\rho=\text { density of the fluid }$
   V= Volume of the solid body immersed in the liquid or Volume of the fluid displaced

3. Relative density of a body

   $R . D=\frac{\text { density of body }}{\text { density of water }}$

4. Bernoulli's equation $P+\rho g h+\frac{1}{2} \rho v^2=\text { constant }$

   $P \rightarrow$ Pressure energy per unit volume $\rho g h \rightarrow$ Potential Energy per unit volume $\frac{1}{2} \rho v^2 \rightarrow$ Kinetic Energy per unit volume

5. Velocity gradient $=\frac{\text { chane in velocity }}{\text { change in height }}$

Kinetic theory of Gases

1. Boyle's law $V \propto \frac{1}{P}$
2. Charle's law $V \propto T$
3. GRAHAM’S LAW OF DIFFUSION

   $r \propto \frac{1}{\sqrt{\rho}} \propto \frac{1}{\sqrt{M}} \propto V_{r m s}$
   Where, $r=$ rate of diffusion of gas
   $\rho=$ Density of the gas
   M = Molecular weight of the gas
   $V_{r m s}=$ Root mean square velocity

4. Ideal gas equation $P V=n R T$

5. Degree of freedom

   $f=3 N-R$
   Where
   $N=$ no. of particle
   $R=$ no. of relation

Thermodynamics

1. $\Delta W=P \Delta V=P\left(V_f-V_i\right)$

2. Heat transfer -

   $\begin{aligned}
   & \Delta Q=m L_{\text {(for change of state) }} \\
   & \Delta Q=m s \Delta T \text { (for change in temperature) }
   \end{aligned}$

3. First law of thermodynamics $\Delta Q=\Delta U+\Delta W$

4. Efficiency of Heat Engine $\eta=\frac{\text { Work done }}{\text { Heat input }}=\frac{W}{Q_1}$

5. Entropy $d S=\frac{\text { Heat absorbed by system }}{\text { Absolute temperature }}$ or $d S=\frac{d Q}{T}$

Oscillations

1. General equation of SHM

   1. For Displacement:-
   $x=A \operatorname{Sin}(w t+\phi) ;$ where $\phi$ is initial phase or epoch and $(\omega t+\phi)$ is called as phase.
   Various displacement equations:-
   (1) $x=A$ Sin $\omega t \Rightarrow$ when particle starts from mean position towards right.
   (2) $x=-$ ASinwt $\Rightarrow$ when particle starts from mean position towards left.
   (3) $x=A C o s w t \Rightarrow$ when particle starts from right extreme position towards left
   (4) $x=-$ ACoswt $\Rightarrow$ when particle starts from left extreme position towards Right.
   2. For Velocity (v):-

   $$
   \begin{aligned}
   x & =A \operatorname{Sin}(\omega t+\phi) \\
   \Rightarrow v & =\frac{d x}{d t}=A \omega \operatorname{Cos}(\omega t+\phi)=A \omega \operatorname{Sin}\left(\omega t+\phi+\frac{\pi}{2}\right)
   \end{aligned}
   $$

   3. For Acceleration:-

   $$
   \begin{aligned}
   x & =A \operatorname{Sin}(\omega t+\phi) \\
   \Rightarrow v & =\frac{d x}{d t}=A \omega \operatorname{Cos}(\omega t+\phi)=A \omega \operatorname{Sin}\left(\omega t+\phi+\frac{\pi}{2}\right) \\
   \Rightarrow a & =\frac{d v}{d t}=-A \omega^2 \operatorname{Sin}(\omega t+\phi)=A \omega^2 \operatorname{Sin}(\omega t+\phi+\pi)=-\omega^2 x
   \end{aligned}
   $$

2. Differential equation of SHM $\begin{aligned} & \frac{d v}{d t}=-\omega^2 x \\ & \Rightarrow \frac{d}{d t}\left(\frac{d x}{d t}\right)=-\omega^2 x \\ & \Rightarrow \frac{d^2 x}{d t^2}+\omega^2 x=0\end{aligned}$

3. Kinetic Energy $K=\frac{1}{2} m v^2$

4. Spring Force $F=-k x$

Electric Charges and Fields

1. Coulomb's Law $F=\frac{K Q_1 Q_2}{r^2}$
2. Electric Field Intensity $E=\frac{F}{q_0}$
3. Linear charge distribution $\lambda=\frac{q}{L}=\frac{C}{m}=C m^{-1}$
4. Surface charge distribution $\sigma=\frac{Q}{A}=\frac{C}{m^2}=C m^{-2}$
5. Volume Charge distribution $\rho=\frac{Q}{V}=\frac{C}{m^3}=C m^{-3}$
6. Electric Dipole $(\vec{P})=q(2 \vec{l})$
7. Torque on dipole $\tau=Q E d \sin \theta$
8. Electric flux $\phi=\int \vec{E} \cdot \vec{d} A$
9. Gauss's law $\phi=\oint E \cdot d A$

Electrostatic Potential and Capacitance

1. Electric Potential $V=\frac{W_{e x t}}{q_0}$
2. Electrostatic Potential energy (U) $U=\frac{K Q q}{r}$
3. Capacitance $C=\frac{Q}{V}$
4. Series combination $C=\frac{c_1 c_2}{c_1+c_2}$
5. Parallel combination $\mathbf{C}=c_1+c_2+c_3$
6. Energy stored in capacitor $U=\frac{1}{2} \frac{Q^2}{C}=\frac{1}{2} Q V=\frac{1}{2} C V^2$

Current Electricity

1. $I=\frac{Q}{t}$
2. Current Density $\bar{j}=\frac{\Delta i}{\Delta A}$
3. Drift Velocity $v_d=\frac{-e \vec{E}}{m} \tau$
4. Ohm’s law $V=I R$
5. Mobility $\mu=\frac{v_d}{E}$
6. Resistance $R=\rho \frac{l}{A}$
7. Specific Resistance $(\rho)$ $\rho=\frac{m}{n e^2 \tau}$
8. Series grouping of Resistance $R_{e q}=R_1+R_2+R_3+\cdots+R_n$
9. Parallel Grouping Of Resistance $\frac{1}{R_{e q}}=\frac{1}{R_1}+\frac{1}{R_2}+\cdots+\frac{1}{R_n}$
10. Kirchoff's first law $i_1+i_3=i_2+i_4$
11. Kirchoff's second law $-i_1 R_1+i_2 R_2-E_1-i_3 R_3+E_2+E_3-i_4 R_4=0$

Moving Charges and Magnetism

1. Biot-Savart Law $d B=K \frac{I d l \sin \theta}{r^2}$
2. Ampere's Circuital Law $\oint \vec{B} d \vec{l}=\mu_0 \sum i$
3. Magnetic Feild of Toroid $\mathrm{B}=\frac{\mu_0 \mathrm{NI}}{2 \pi r}$
4. Lorentz Force $\vec{F}=q[\vec{E}+(\vec{v} \times \vec{B})]$
5. Current sensitivity (S_i) $S_i=\frac{\alpha}{i}=\frac{N B A}{C}$
6. Voltage sensitivity (S_V) $S_V=\frac{\alpha}{V}=\frac{\alpha}{i R}=\frac{S_i}{R}=\frac{N B A}{R C}$

Magnetism and Matter

1. Magnetic flux $\phi_B=\int \vec{B} \cdot d \vec{S}$
2. Magnetic Intensity $H=\frac{B_0}{\mu_0}$

Electromagnetic Induction

1. Faraday's Law: Rate of change of magnetic Flux= $\varepsilon=\frac{-d \phi}{d t}$ where $d \phi \rightarrow \phi_2-\phi_{1=}$ change in flux
2. Induced Current $I=\frac{\varepsilon}{R}=\frac{-N}{R} \frac{d \phi}{d t}$
3. Induced Charge $d q=i . d t=\frac{-N}{R} \frac{d \phi}{d t} . d t$
4. Induced Power $P=\frac{\varepsilon^2}{R}=\frac{N^2}{R}\left(\frac{d \phi}{d t}\right)^2$
5. Induced Electric Field $\varepsilon=\oint \vec{E}_{i n} \cdot \overrightarrow{d l}=\frac{-d \phi}{d t}$
6. Energy Stored In An Inductor $U=\frac{1}{2} L I^2$

Electromagnetic Waves

1. Maxwell's equations 1. $\oint \mathbf{E} \cdot \mathrm{d} \mathbf{A}=\mathrm{Q} / \varepsilon_0$
   (Gauss's Law for electricity)
   2. $\oint \mathbf{B} \cdot \mathrm{d} \mathbf{A}=0$
   (Gauss's Law for magnetism)
   3. $\oint \mathbf{E} \cdot \mathrm{d} \mathbf{l}=\frac{-\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{d} t}$
   (Faraday's Law)
   4. $\oint \mathbf{B} \cdot \mathrm{d} \mathbf{l}=\mu_0 i_{\mathrm{c}}+\mu_0 \varepsilon_0 \frac{\mathrm{~d} \phi_E}{\mathrm{~d} t}$
   (Ampere-Maxwell Law)
2. Intensity (I) $I=\frac{\text { Total EM energy }}{\text { Surface area } \times \text { Time }}=\frac{\text { Total energy density } \times \text { Volume }}{\text { Surface area } \times \text { Time }}$
3. Wavelength of EM Wave

   $\lambda=\frac{\lambda_o}{\mu}$

   $\lambda_o=$ Wavelength in vacuum
   $\mu$ = Refractive index of medium

Ray Optics and Optical Instruments

1. Mirror formula $f=\frac{1}{u}+\frac{1}{v}$
2. lateral magnification $m_v=\frac{\text { height of image }}{\text { height of object }}=\frac{h_i}{h_0}$
3. Refractive index $\mu=\frac{c}{v}$
4. Magnifying power $m=\frac{\text { Visual angle with instrument }(\beta)}{\text { Visual angle when object is placed at least distance of distinct vision }(\alpha)}$

Dual Nature of Matter and Radiation

1. Work function $\phi=h \nu_o=\frac{h c}{\lambda_o}$
2. $E=h \nu=\frac{h c}{\lambda}$
3. Momentum of the photon $p=m \times c=\frac{E}{c}=\frac{h \nu}{c}=\frac{h}{\lambda}$
4. Einstein's Photoelectric Equation K.E. $=h v-\Phi$
5. Photon Flux $\phi=\frac{\text { Intensity }}{\text { Energy of each photon }}=\frac{I}{E}=\frac{n}{A}$
6. De Broglie’s Equation $\lambda=\frac{h}{p}$

Also Read: JEE Main 2026 Important Formulas for Physics PDF

JEE Main Formulas for Chemistry 2026

Candidates while studying the chemistry, they need to revise and practice the chemical equations and symbols, to some chemistry is tough subject but when candidates practices chemical equations, revises the properties, formulas and symbols they will have command over the subject Candidates can check the JEE Main Chemistry formulas below

JEE Main Important Formulas of Physical Chemistry

Some Basic Concepts in chemistry

1. Boyle's Law: $P_1 V_1=P_2 V_2$ (at constant T and n )
2. Charles's Law: $\frac{V_1}{T_1}=\frac{V_2}{T_2}($ at constant P and n$)$
3. Avogadro's Law: $\frac{V}{n}=$ constant
4. Average Atomic Mass $=\frac{\Sigma(\text { Mass of Isotopes })_i \times(\% \text { abundance })_i}{100}$
5. Mole $=\frac{\mathrm{W}}{\mathrm{M}}=\frac{(\mathrm{Wt} . \text { of substance in gm. })}{(\text { Molar mass of substance }(\mathrm{G} . \mathrm{m} . \mathrm{m}))}$
6. Mass $\%$ of an element $=\frac{\text { Mass of that element in one mole of the compound }}{\text { Molar mass of the compound }} \times 100$
7. Equivalent Weight $=\frac{\text { Molecular weight }}{\mathrm{n}-\text { factor }(\mathrm{x})}$

Atomic Structure

1. Frequency $\nu=\frac{1}{\mathrm{~T}}$
2. Wave number $(\bar{\nu})$ $\bar{\nu}=\frac{1}{\lambda}$
3. $E=h \nu=\frac{h c}{\lambda}$

4. Line Spectrum of Hydrogen-like atoms

   $\frac{1}{\lambda}=R Z^2\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)$

5. Bohr radius of nth orbit:

   $\mathrm{r}_{\mathrm{n}}=0.529 \frac{\mathrm{n}^2}{\mathrm{Z}} \mathrm{~A}^0$

6. Velocity of electron in nth orbit:

   $\mathrm{V}_{\mathrm{n}}=\left(2.18 \times 10^6\right) \frac{\mathrm{Z}}{\mathrm{n}} \mathrm{~m} / \mathrm{s}$

   where Z is atomic number

7. Total energy of electron in nth orbit:

   $\mathrm{E}_{\mathrm{n}}=-13.6 \frac{\mathrm{Z}^2}{\mathrm{n}^2} \mathrm{eV}=-2.18 \times 10^{-18} \frac{\mathrm{Z}^2}{\mathrm{n}^2} \mathrm{~J}$

   where Z is the atomic number

8. Heisenberg Uncertainty Principle: $\Delta x . \Delta P \geq \frac{h}{4 \pi}$

9. $\mathrm{E}_{\mathrm{n}}=-\frac{1312 \times \mathrm{Z}^2}{\mathrm{n}^2} \mathrm{~kJ} / \mathrm{mol}$

Chemical Thermodynamics

1. Expansion Work $=\mathrm{P} \times \Delta \mathrm{V}=-\mathrm{P}_{\text {ext. }}\left[\mathrm{V}_2-\mathrm{V}_1\right]$
   $\mathrm{P}=$ external pressure And $\Delta \mathrm{V}=$ increase or decrease in volume.

2. Work done in a reversible isothermal process

   $\begin{aligned}
   & \mathrm{W}=-2.303 \mathrm{nRT} \log _{10} \frac{\mathrm{~V}_2}{\mathrm{~V}_1} \\
   & \mathrm{~W}=-2.303 \mathrm{nRT} \log _{10} \frac{\mathrm{P}_1}{\mathrm{P}_2}
   \end{aligned}$

3. Work done in an irreversible isothermal process
   Work $=-\mathrm{P}_{\text {ext. }}\left(\mathrm{V}_2-\mathrm{V}_1\right)$
   That is, Work $=-\mathrm{P} \times \Delta \mathrm{V}$

4. $W=\Delta E=n C_V \Delta T$

5. Enthalpy: $H=U+p V$

6. First Law of Thermodynamics: $\Delta U=q+W$

7. $\Delta \mathrm{G}=\Delta \mathrm{H}-\mathrm{T} \Delta(\mathrm{S})$

8. $\Delta G=-n F E$

Equilibrium

1. For a reaction:

   $\mathrm{mA}+\mathrm{nB} \rightleftharpoons \mathrm{pC}+\mathrm{qD}$ $\frac{\mathrm{K}_{\mathrm{f}}}{\mathrm{K}_{\mathrm{b}}}=\frac{[\mathrm{C}]^{\mathrm{p}}[\mathrm{D}]^{\mathrm{q}}}{[\mathrm{A}]^{\mathrm{m}}[\mathrm{B}]^{\mathrm{n}}}=\mathrm{K}_{\mathrm{c}}$

2. $\mathrm{pH}=-\log _{10}\left[\mathrm{H}^{+}\right]$

3. $\mathrm{k}_{\mathrm{w}}=\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right]=10^{-14}$

4. $\mathrm{pH}=\mathrm{pK}_{\mathrm{a}}+\log _{10} \frac{[\text { Salt }]}{\text { Acid }}$

5. $\mathrm{pOH}=\mathrm{pK}_{\mathrm{b}}+\log _{10} \frac{[\text { Salt }]}{[\text { Base }]}$

ELECTROCHEMISTRY

1. $\mathrm{W}=\frac{\text { Eit }}{96500}$

2. $\begin{aligned}
   & \frac{E_1}{E_2}=\frac{M_1}{M_2} \text { or } \frac{W_1}{W_2}=\frac{Z_1}{Z_2} \\
   & E_1=\text { equivalent weight } \\
   & E_2=\text { equivalent weight }
   \end{aligned}$
   W or M = mass deposited

3. $\begin{aligned} & E_{\text {cell }} \text { or } E M F=\left[E_{\text {red }}(\text { cathode })-E_{\text {red }}(\text { anode })\right] \\ & E_{\text {eell }}^{\circ} \text { or } E M F^{\circ} \\ & =\left[E_{\text {red }}^{\circ}(\text { cathode })-E_{\text {red }}^{\circ}(\text { anode })\right]\end{aligned}$

4. $\mathrm{E}=\mathrm{E}^{\circ}-\frac{\mathrm{RT}}{\mathrm{nF}} \ln Q$

5. $\mathrm{xA}+\mathrm{yB} \xrightarrow{\mathrm{ne}^{-}} \mathrm{mC}+\mathrm{nD}$
   The emf can be calculated as

   $\text { Ecell }=\mathrm{E}^{\circ} \text { cell }-\frac{0.059}{\mathrm{n}} \log \frac{[\mathrm{C}]^{\mathrm{m}}[\mathrm{D}]^{\mathrm{n}}}{[\mathrm{~A}]^x[\mathrm{~B}]^{\mathrm{y}}}$

6. $\wedge_{\mathrm{m}}=\kappa \times \frac{1000}{\mathrm{c}}$

7. $\wedge_{\text {eq }}=\frac{1000 \times \kappa}{\mathrm{N}}$

Solutions

1. Mass $\%$ of a component $=\frac{\text { Mass of the component in the solution }}{\text { Total mass of the solution }} \times 100$
2. Volume $\%$ of a component $=\frac{\text { Volume of the component }}{\text { Total volume of solution }} \times 100$
3. Mass by Volume $\%$ of a component $=\frac{\text { Mass of the component }}{\text { Total volume of solution }} \times 100$
4. Parts per million $=\frac{\text { Number of parts of the component }}{\text { Total number of parts of all components of the solution }} \times 10^6$
5. Mole fraction of a component $=\frac{\text { Number of moles of the component }}{\text { Total number of moles of all the components }}$
6. Molarity: $(M)=\frac{\text { No. of Moles of Solutes }}{\text { Volume of Solution in Liters }}$
7. Molality: $(m)=\frac{\text { No. of Moles of Solutes }}{\text { Mass of solvent in } \mathrm{kg}}$
8. $\left(P_T\right)=P_A^o X_A+P_B^o X_B$ ($\begin{aligned} & P_A=P_A^o X_A \\ & P_B=P_B^o X_B \\ & P_T=P_A+P_B\end{aligned}$)
9. $\Delta \mathrm{T}_{\mathrm{b}}=\mathrm{K}_{\mathrm{b}} \times \frac{\mathrm{w}}{\mathrm{M}} \times \frac{1000}{\mathrm{~W}}$
10. $\Delta T_f=K_f \times \frac{w}{M} \times \frac{1000}{W}$
11. $\Pi=C R T$
12. $\begin{aligned} & \mathrm{i}=\frac{\text { Observed number of solute particles }}{\text { Number of particles initially taken }} \\ & \mathrm{i}=\frac{\text { Observed value of colligative property }}{\text { Theoretical value of colligative property }}\end{aligned}$

Chemical kinetics

1. Unit of average velocity $=\frac{\text { Unit of concentration }}{\text { Unit of time }}=\frac{\text { mole }}{\text { litre second }}=$ mole litre $^{-1}$ second $^{-1}$
2. $\mathrm{aA}+\mathrm{bB} \rightarrow \mathrm{cC}+\mathrm{dD}$
   Rate w.r.t. $[\mathrm{A}]=-\frac{\mathrm{d}[\mathrm{A}]}{\mathrm{dt}} \times \frac{1}{\mathrm{a}}$
   Rate w.r.t. $[B]=-\frac{d[B]}{d t} \times \frac{1}{b}$
   Rate w.r.t. $[\mathrm{C}]=-\frac{\mathrm{d}[\mathrm{C}]}{\mathrm{dt}} \times \frac{1}{\mathrm{c}}$
   Rate w.r.t. $[\mathrm{D}]=-\frac{\mathrm{d}[\mathrm{D}]}{\mathrm{dt}} \times \frac{1}{\mathrm{~d}}$
3. $\mathrm{R} \propto[\mathrm{A}]^{\mathrm{p}}[\mathrm{B}]^{\mathrm{q}}$

4. Unit of Rate Constant-

   $\begin{aligned}
   & \text { The differential rate expression for } \mathrm{n}^{\text {th }} \text { order reaction is as follows: } \\
   & \qquad-\frac{\mathrm{dx}}{\mathrm{dt}}=\mathrm{k}(\mathrm{a}-\mathrm{x})^{\mathrm{n}} \\
   & \text { or } \quad \mathrm{k}=\frac{\mathrm{dx}}{(\mathrm{a}-\mathrm{x})^{\mathrm{n}} \mathrm{dt}}=\frac{(\text { concentration })}{(\text { concentration })^{\mathrm{n}} \text { time }}=(\text { conc. })^{1-\mathrm{n}} \text { time }^{-1}
   \end{aligned}$

5. For the first-order reaction,

   $k=\frac{2.303}{t} \log \frac{[\mathrm{R}]_0}{[\mathrm{R}]}$

6. $t_{1 / 2}=\frac{0.693}{k}$

7. For any general nth order reaction, it is evident that,

   $\mathrm{t}_{\frac{1}{2}} \propto[\mathrm{~A}]_0^{1-\mathrm{n}}$
   It is to be noted that the above formula is applicable for any general nth-order reaction except $\mathrm{n}=1$.

8. Arrhenius Equation: $\mathrm{k}=\mathrm{Ae}^{-\mathrm{Ea} / \mathrm{RT}}$

9. $\log \frac{\mathrm{K}_2}{\mathrm{~K}_1}=\frac{\mathrm{Ea}}{2.303 \mathrm{R}}\left[\frac{1}{\mathrm{~T}_1}-\frac{1}{\mathrm{~T}_2}\right]$

JEE Main Important Formulas of Inorganic Chemistry

Coordination Compounds

1. $\mathrm{EAN}=Z-O+2 L$
   Where:
   $\mathbf{Z}=$ Atomic number of the central metal atom/ion
   $\mathbf{O}=$ Oxidation state of the metal atom/ion
   L = Number of ligands (or donor atoms) $\times$ number of electrons donated per ligand

2. Crystal Field Stabilization Energy (CFSE):
   Octahedral:

   $\mathrm{CFSE}=(-0.4 x+0.6 y) \Delta_0$

   Tetrahedral:

   $\mathrm{CFSE}=(-0.6 x+0.4 y) \Delta_t$

   where $x=t_2 g$ electrons, $y=$ e_g electrons

d- & f-Block Elements

1. Magnetic Moment:

   $\mu=\sqrt{n(n+2)} \mathrm{BM}$

Chemical Bonding and Molecular Structure

1. Formal Charge:

   $\text { F.C. }=V-N-\frac{B}{2}$

   ( $\mathrm{V}=$ valence electrons, $\mathrm{N}=$ non-bonding, $\mathrm{B}=$ bonding electrons)

2. Bond Order (Molecular Orbital Theory):

   $\text { Bond Order }=\frac{\left(N_b-N_a\right)}{2}$

3. Dipole Moment:

   $\mu=q \times d$

   ( $q=$ charge,$d=$ distance between charges)

JEE Main Important Formulas: Inorganic Chemistry

Some Basic Principles of Organic Chemistry

1. Application of Inductive Effect

   The decreasing -I effect or increasing +I effect order is as follows:

   $\begin{aligned}
   & -\mathrm{NH}_3+>-\mathrm{NO}_2>-\mathrm{SO}_2 \mathrm{R}>-\mathrm{CN}>-\mathrm{SO}_3 \mathrm{H}>-\mathrm{CHO}>-\mathrm{CO}>-\mathrm{COOH}>-\mathrm{F}>-\mathrm{COCl}>-\mathrm{CONH}_2>-\mathrm{Cl}>-\mathrm{Br}>-\mathrm{I}>-\mathrm{OR}>-\mathrm{OH}>-\mathrm{NR}_2>-\mathrm{NH}_2> \\
   & -\mathrm{C}_6 \mathrm{H}_5>-\mathrm{CH}=\mathrm{CH}_2>-\mathrm{H}
   \end{aligned}$

2. Degree of Unsaturation (DU or IHD):

   $\mathrm{DU}=\frac{2 C+2-H+N-X}{2}$

   ( $\mathrm{C}=$ carbon, $\mathrm{H}=$ hydrogen, $\mathrm{N}=$ nitrogen, $\mathrm{X}=$ halogen)

Hydrocarbons

1. Alkanes: $C_n H_{2 n+2}$
2. Alkenes: $C_n H_{2 n}$
3. Alkynes: $C_n H_{2 n-2}$

Carboxylic Acids and Derivatives

Method of Preparation of Carboxylic Acid

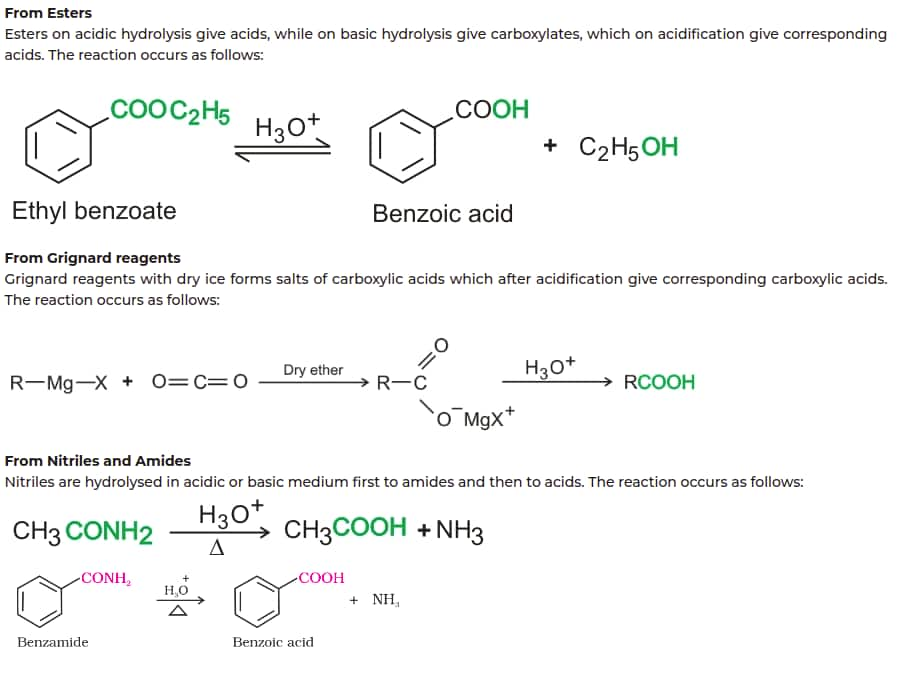
Also Read: JEE Main 2026 Chemistry Important Formulas PDF

JEE Main formulas for Maths 2026

Candidates must go through all the formulas and practice the mathematical problems. Without formulas you cannot solve any problem though you know how to solve it. Revising the formulas daily is very important. Here we have provided the Mathematics formulas for JEE Mains.

Sets, Relations, and Functions

1. Properties of union $\mathrm{A} \cup \mathrm{B}=\mathrm{B} \cup \mathrm{A} \quad$ (Commutative Property)
   $(\mathrm{A} \cup \mathrm{B}) \cup \mathrm{C}=\mathrm{A} \cup(\mathrm{B} \cup \mathrm{C})$ (Associative property)
   $\mathrm{A} \cup \varphi=\mathrm{A}$ (Law of identity element, $\varphi$ is the identity of Null Set)
   $\mathrm{A} \cup \mathrm{A}=\mathrm{A}$ (Idempotent law)
   $\mathrm{U} \cup \mathrm{A}=\mathrm{U}($ Law of U$)$
   If A is a subset of B , then $\mathrm{A} \cup \mathrm{B}=\mathrm{B}$
2. Properties of intersection $\mathrm{A} \cap \mathrm{B}=\mathrm{B} \cap \mathrm{A}$ (Commutative law).
   $(\mathrm{A} \cap \mathrm{B}) \cap \mathrm{C}=\mathrm{A} \cap(\mathrm{B} \cap \mathrm{C})$ (Associative law).
   $\mathrm{A} \cap \phi=\phi$,
   $\mathrm{A} \cap \mathrm{U}=\mathrm{A}$ (Law of $\phi$ and U ).
   $\mathrm{A} \cap \mathrm{A}=\mathrm{A}$ (Idempotent law)
   If A is subset of B , then $\mathrm{A} \cap \mathrm{B}=\mathrm{A}$
3. Properties of Difference of Sets 1. In general A - B does not equal B - A
   2. $\mathrm{A}-\mathrm{A}=\phi$
   3. $\mathrm{A}-\phi=\mathrm{A}$
   4. $\mathrm{A}-\mathrm{U}=\phi$
   5. If A is a subset of B , then $\mathrm{A}-\mathrm{B}=\phi$
4. Symmetric Difference of Sets ( A Δ B ) $A \Delta B=(A-B) \cup(B-A)$
5. Properties of Compliment $\begin{aligned} & A \cup A^{\prime}=U \\ & A \cap A^{\prime}=\varphi \\ & \left(A^{\prime}\right)^{\prime}=A \\ & U^{\prime}=\varphi \text { and } \varphi^{\prime}=U \\ & A-B=A \cap B^{\prime}\end{aligned}$

Complex Numbers and Quadratic Equations

1. Equality of Complex Numbers $a+i b=c+i d$
2. Addition of Two Complex Numbers $z_1+z_2=(a+i b)+(c+i d)=(a+c)+i(b+d)$
3. Difference of Two Complex Numbers $z_1-z_2=(a+i b)-(c+i d)=(a-c)+i(b-d)$
4. Multiplication of Two Complex Numbers $z_1 \times z_2=(a+i b)(c+i d)$
5. Division of Two Complex Numbers $\frac{z_1}{z_2}=\frac{a+i b}{c+i d} \cdot \frac{c-i d}{c-i d}$
6. Modulus $|z|=\sqrt{x^2+y^2}$

Matrices and Determinants

1. Addition of matrices $A=\left[a_{i j}\right]_{m \times n}, B=\left[b_{i j}\right]_{m \times n}$ Then, $A+B=\left[a_{i j}+b_{i j}\right]_{m \times n}$ for all $i, j$
2. Subtraction of matrices $A=\left[a_{i j}\right]_{m \times n}, B=\left[b_{i j}\right]_{m \times n}$ Then, $A-B=\left[a_{i j}-b_{i j}\right]_{m \times n}$ for all $i, j$
3. Multiplication of Determinant $\Delta_1=\left|\begin{array}{lll}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3\end{array}\right|$ and $\Delta_2=\left|\begin{array}{ccc}\alpha_1 & \beta_1 & \gamma_1 \\ \alpha_2 & \beta_2 & \gamma_2 \\ \alpha_3 & \beta_3 & \gamma_3\end{array}\right|$ then $\Delta_1 \times \Delta_2=\left|\begin{array}{lll}a_1 \alpha_1+b_1 \beta_1+c_1 \gamma_1 & a_1 \alpha_2+b_1 \beta_2+c_1 \gamma_2 & a_1 \alpha_3+b_1 \beta_3+c_1 \gamma_3 \\ a_2 \alpha_1+b_2 \beta_1+c_2 \gamma_1 & a_2 \alpha_2+b_2 \beta_2+c_2 \gamma_2 & a_2 \alpha_3+b_2 \beta_3+c_2 \gamma_3 \\ a_3 \alpha_1+b_3 \beta_1+c_3 \gamma_1 & a_3 \alpha_2+b_3 \beta_2+c_3 \gamma_2 & a_3 \alpha_3+b_3 \beta_3+c_3 \gamma_3\end{array}\right|$

Sequence and Series

1. Series $\mathrm{S}_{\mathrm{n}}=a_1+a_2+a_3+\ldots \ldots \ldots .+a_n=\sum_{\mathrm{r}=1}^{\mathrm{n}} a_r=\sum a_r$
2. General Term of an AP $\begin{aligned} & a_1=a+(1-1) d=a \\ & a_2=a+(2-1) d=a+d \\ & a_3=a+(3-1) d=a+2 d \\ & a_4=a+(4-1) d=a+3 d\end{aligned}$
3. Arithmetic Mean $A=\frac{a_1+a_2+a_3+\ldots . .+a_n}{n}$.
4. .General Term of a GP $\begin{aligned} & a_1=a=a r^{1-1} \quad\left(1^{\text {st }} \text { term }\right) \\ & a_2=a r=a r^{2-1} \quad\left(2^{\text {nd }} \text { term }\right) \\ & a_3=a r^2=a r^{3-1} \quad\left(3^{\text {rd }} \text { term }\right)\end{aligned}$
5. Geometric Mean $G=\sqrt[n]{a_1 \cdot a_2 \cdot a_3 \cdot \ldots . . \cdot a_n}$
6. Sum of n-term of a GP $S_n=a\left(\frac{r^n-1}{r-1}\right)$
7. .Sum of an infinite GP $\mathrm{S}_{\infty}=\frac{\mathrm{a}}{1-\mathrm{r}}$
8. Harmonic Mean
9. $H=\frac{n}{\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}+\ldots .+\frac{1}{a_n}}$

Trigonometry

1. Trigonometric Functions of Acute Angles $\begin{aligned} & \text { Sine } \quad \sin t=\frac{\text { opposite }}{\text { hypotenuse }} \\ & \text { Cosine } \quad \cos t=\frac{\text { adjacent }}{\text { hypotenuse }} \\ & \text { Tangent } \quad \tan t=\frac{\text { opposite }}{\text { adjacent }}\end{aligned}$
2. Trigonometric Identities $\begin{aligned} & \sin ^2 t+\cos ^2 t=1 \\ & 1+\tan ^2 t=\sec ^2 t \\ & 1+\cot ^2 t=\csc ^2 t \\ & \tan t=\frac{\sin t}{\cos t}, \quad \cot t=\frac{\cos t}{\sin t}\end{aligned}$
3. Trigonometric Ratio for Compound Angles $\begin{aligned} & \cos (\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta \\ & \cos (\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta \\ & \sin (\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta \\ & \sin (\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\end{aligned}$$\begin{aligned} \tan (\alpha+\beta) & =\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta} \\ \tan (\alpha-\beta) & =\frac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta} \\ \cot (\alpha+\beta) & =\frac{\cot \alpha \cot \beta-1}{\cot \alpha+\cot \beta} \\ \cot (\alpha-\beta) & =\frac{\cot \alpha \cot \beta+1}{\cot \beta-\cot \alpha}\end{aligned}$
4. Product into Sum/Difference 1. $2 \cos \alpha \cos \beta=[\cos (\alpha-\beta)+\cos (\alpha+\beta)]$
   2. $2 \sin \alpha \sin \beta=[\cos (\alpha-\beta)-\cos (\alpha+\beta)]$
   3. $2 \sin \alpha \cos \beta=[\sin (\alpha+\beta)+\sin (\alpha-\beta)]$
   4. $2 \cos \alpha \sin \beta=[\sin (\alpha+\beta)-\sin (\alpha-\beta)]$
5. Sum/Difference into Product 1. $\sin \alpha+\sin \beta=2 \sin \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\alpha-\beta}{2}\right)$
   2. $\sin \alpha-\sin \beta=2 \sin \left(\frac{\alpha-\beta}{2}\right) \cos \left(\frac{\alpha+\beta}{2}\right)$
   3. $\cos \alpha-\cos \beta=-2 \sin \left(\frac{\alpha+\beta}{2}\right) \sin \left(\frac{\alpha-\beta}{2}\right)$
   4. $\cos \alpha+\cos \beta=2 \cos \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\alpha-\beta}{2}\right)$
6. Reduction Formula $\begin{aligned} \sin ^2 \theta & =\frac{1-\cos (2 \theta)}{2} \\ \cos ^2 \theta & =\frac{1+\cos (2 \theta)}{2} \\ \tan ^2 \theta & =\frac{1-\cos (2 \theta)}{1+\cos (2 \theta)}\end{aligned}$
7. Triple Angle Formula 1. $\sin 3 \mathrm{~A}=3 \sin \mathrm{~A}-4 \sin ^3 \mathrm{~A}$
   2. $\cos 3 \mathrm{~A}=4 \cos ^3 \mathrm{~A}-3 \cos A$
   3. $\tan 3 \mathrm{~A}=\frac{3 \tan \mathrm{~A}-\tan ^3 \mathrm{~A}}{1-3 \tan ^2 \mathrm{~A}}$
8. Half Angle Formula 1. $\sin \left(\frac{\alpha}{2}\right)= \pm \sqrt{\frac{1-\cos \alpha}{2}}$
   2. $\quad \cos \left(\frac{\alpha}{2}\right)= \pm \sqrt{\frac{1+\cos \alpha}{2}}$
   3. $\tan \left(\frac{\alpha}{2}\right)= \pm \sqrt{\frac{1-\cos \alpha}{1+\cos \alpha}}$

Co-ordinate Geometry

1. Internal division $\mathbf{x}=\frac{\mathbf{m x}_2+\mathbf{n} \mathbf{x}_1}{\mathbf{m}+\mathbf{n}}, \mathbf{y}=\frac{\mathbf{m y}_2+\mathbf{n y}_1}{\mathbf{m}+\mathbf{n}}$
2. External Division $\mathbf{x}=\frac{\mathbf{m x}_2-\mathbf{n x}_1}{\mathbf{m}-\mathbf{n}}, \quad \mathbf{y}=\frac{\mathbf{m y}_2-\mathbf{n y}_1}{\mathbf{m}-\mathbf{n}}$
3. Parametric Form for $(x-h)^2+(y-k)^2=\mathbf{r}^2$

Limit, Continuity And Differentiability

1. Sum law for limits : $\lim _{x \rightarrow a}(f(x)+g(x))=\lim _{x \rightarrow a} f(x)+\lim _{x \rightarrow a} g(x)=L+M$
2. Difference law for limits : $\lim _{x \rightarrow a}(f(x)-g(x))=\lim _{x \rightarrow a} f(x)-\lim _{x \rightarrow a} g(x)=L-M$
3. Constant multiple law for limits : $\lim _{x \rightarrow a} c f(x)=c \cdot \lim _{x \rightarrow a} f(x)=c L$
4. Product law for limits : $\lim _{x \rightarrow a}(f(x) \cdot g(x))=\lim _{x \rightarrow a} f(x) \cdot \lim _{x \rightarrow a} g(x)=L \cdot M$
5. Quotient law for limits : $\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\frac{\lim _{x \rightarrow a} f(x)}{\lim _{x \rightarrow a} g(x)}=\frac{L}{M}$ for $M \neq 0$
6. Binomial Expansion for any index

   $(1+x)^n=1+n x+\frac{n(n-1)}{2!} x^2+\frac{n(n-1)(n-2)}{3!} x^3 \ldots$

   where, $|x|<1$

7. DIFFERENTIATION $\frac{d}{d x}($ constant $)=0$ $\frac{d}{d x}\left(\mathbf{x}^{\mathbf{n}}\right)=\mathbf{n} \mathbf{x}^{\mathbf{n}-\mathbf{1}}$ $\frac{d}{d x}\left(\mathbf{a}^{\mathbf{x}}\right)=\mathbf{a}^{\mathbf{x}} \log _{\mathrm{e}} \mathbf{a}$

   $\frac{d}{d x}\left(\mathbf{e}^{\mathbf{x}}\right)=\mathbf{e}^{\mathbf{x}} \log _{\mathbf{e}} \mathbf{e}=\mathbf{e}^{\mathbf{x}}$

   $\frac{d}{d x}\left(\log _{\mathbf{a}}|\mathbf{x}|\right)=\frac{1}{\mathbf{x} \log _{\mathbf{e}} \mathbf{a}}, \quad \mathbf{x} \neq \mathbf{0}$
   $\frac{d}{d x}\left(\log _{\mathrm{e}}|\mathbf{x}|\right)=\frac{1}{\mathbf{x}}, \quad \mathbf{x} \neq \mathbf{0}$

8. Sum Rule $\frac{d}{d x}(f(x)+g(x))=\frac{d}{d x}(f(x))+\frac{d}{d x}(g(x))$

9. Difference Rule $\frac{d}{d x}(f(x)-g(x))=\frac{d}{d x}(f(x))-\frac{d}{d x}(g(x))$

10. Constant Multiple Rule $\frac{d}{d x}(k f(x))=k \frac{d}{d x}(f(x))$

11. Product Rule $\frac{d}{d x}(f(x) g(x))=g(x) \cdot \frac{d}{d x}(f(x))+f(x) \cdot \frac{d}{d x}(g(x))$

Integral Calculus

1. Rules of integration (a) $\int \mathrm{kf}(x) d x=k \int f(x) d x$ for any constant $k$.
   (b) $\int(f(x)+g(x)) d x=\int f(x) d x+\int g(x) d x$
   (c) $\int(f(x)-g(x)) d x=\int f(x) d x-\int g(x) d x$
2. Trigonometric Functions 1. $\frac{d}{d x}(-\cos x)=\sin x \Rightarrow \int \sin x d x=-\cos x+C$
   2. $\frac{d}{d x}(\sin x)=\cos x \Rightarrow \int \cos x d x=\sin x+C$
   3. $\frac{\mathrm{d}}{\mathrm{dx}}(\tan \mathrm{x})=\sec ^2 \mathrm{x} \Rightarrow \int \sec ^2 \mathrm{x} \mathrm{dx}=\tan \mathrm{x}+\mathrm{C}$
   4. $\frac{\mathrm{d}}{\mathrm{dx}}(-\cot \mathrm{x})=\csc ^2 \mathrm{x} \Rightarrow \int \csc ^2 \mathrm{x} \mathrm{dx}=-\cot \mathrm{x}+\mathrm{C}$
   5. $\frac{d}{d x}(\sec x)=\sec x \tan x \Rightarrow \int \sec x \tan x d x=\sec x+C$
   6. $\frac{\mathrm{d}}{\mathrm{dx}}(-\csc \mathrm{x})=\csc \mathrm{x} \cot \mathrm{x} \Rightarrow \int \csc \mathrm{x} \cot \mathrm{x} \mathrm{dx}=-\csc \mathrm{x}+\mathrm{C}$

Differential Equations

1. (i) $\frac{d y}{d x}=\sin 2 x+\cos x$
   (ii) $\mathrm{k} \frac{\mathrm{d}^2 \mathrm{y}}{\mathrm{dx}^2}=\left[1+\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^2\right]^{3 / 2}$

Vector Algebra

1. Unit Vector $\hat{\mathbf{a}}=\frac{\overrightarrow{\mathbf{a}}}{|\overrightarrow{\mathbf{a}}|}$
2. Properties of vector Subtraction 1. $\vec{a}-\vec{b} \neq \vec{b}-\vec{a}$
   2. $(\vec{a}-\vec{b})-\vec{c} \neq \vec{a}-(\vec{b}-\vec{c})$
   3. For any two vectors $\vec{a}$ and $\vec{b}$
   (a) $|\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}|$
   (b) $|\vec{a}+\vec{b}| \geq||\vec{a}|-|\vec{b}||$
   (c) $|\vec{a}-\vec{b}| \leq|\vec{a}|+|\vec{b}|$
   (d) $|\vec{a}-\vec{b}| \geq||\vec{a}|-|\vec{b}||$
3. Linear Combinations of Vectors $\vec{r}=\lambda_1 \vec{a}_1+\lambda_2 \vec{a}_2+\lambda_3 \vec{a}_3+\ldots \ldots+\lambda_n \vec{a}_n$
4. Properties of Dot (Scalar) Product 1. $\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}=\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{a}} \quad$ ( commutative )
   2. $\overrightarrow{\mathbf{a}} \cdot(\overrightarrow{\mathbf{b}}+\overrightarrow{\mathbf{c}})=\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{c}}+\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{c}} \quad$ (distributive)
   3. $\quad(m \overrightarrow{\mathbf{a}}) \cdot \overrightarrow{\mathbf{b}}=m(\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}})=\overrightarrow{\mathbf{a}} \cdot(m \overrightarrow{\mathbf{b}})$; where $m$ is a scalar and $\vec{a}, \vec{b}$ are any two vectors
   4. $\quad(l \overrightarrow{\mathbf{a}}) \cdot(m \overrightarrow{\mathbf{b}})=\operatorname{lm}(\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}})$; where $l$ and $m$ are scalars
5. Angle between two vectors $\begin{aligned} & & \overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}} & =|\overrightarrow{\mathbf{a}}||\overrightarrow{\mathbf{b}}| \cos \theta \\ \Rightarrow & & \cos \theta & =\frac{\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}}{|\overrightarrow{\mathbf{a}}||\overrightarrow{\mathbf{b}}|} \\ \Rightarrow & & \theta & =\cos ^{-1}\left(\frac{\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}}{|\overrightarrow{\mathbf{a}}||\overrightarrow{\mathbf{b}}|}\right)\end{aligned}$
6. Vector Projection Formula Projection of $\overrightarrow{\mathbf{a}}$ on $\overrightarrow{\mathbf{b}}=\frac{\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}}{|\overrightarrow{\mathbf{b}}|}=\overrightarrow{\mathbf{a}} \cdot \frac{\overrightarrow{\mathbf{b}}}{|\overrightarrow{\mathbf{b}}|}=\overrightarrow{\mathbf{a}} \cdot \hat{\mathbf{b}}$ Projection of $\overrightarrow{\mathbf{b}}$ on $\overrightarrow{\mathbf{a}}=\frac{\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}}{|\overrightarrow{\mathbf{a}}|}=\overrightarrow{\mathbf{b}} \cdot \frac{\overrightarrow{\mathbf{a}}}{|\overrightarrow{\mathbf{a}}|}=\overrightarrow{\mathbf{b}} \cdot \hat{\mathbf{a}}$
7. Cross Product of Two Vectors If $\overrightarrow{\mathbf{a}}=a_1 \hat{\mathbf{i}}+a_2 \hat{\mathbf{j}}+a_3 \hat{\mathbf{k}}$ and $\overrightarrow{\mathbf{b}}=b_1 \hat{\mathbf{i}}+b_2 \hat{\mathbf{j}}+b_3 \hat{\mathbf{k}}$, then their cross product given by

   $\vec{a} \times \vec{b}=\left|\begin{array}{lll}
   \hat{i} & \hat{j} & \hat{k} \\
   a_1 & a_2 & a_3 \\
   b_1 & b_2 & b_3
   \end{array}\right|$

Statistics and Probability

1. Mean $\bar{x}=\frac{x_1+x_2+\cdots+x_n}{n}$
2. Mean of the Ungrouped Data $\bar{x}=\frac{x_1+x_2+x_3+\ldots \cdots+x_n}{n}=\frac{1}{n} \sum_{i=1}^n x_i$
3. Mean of Ungrouped Frequency Distribution $\bar{x}=\frac{f_1 x_1+f_2 x_2+f_3 x_3+\ldots \ldots+f_n x_n}{f_1+f_2+f_3+\ldots \ldots+f_n}=\frac{\sum_{i=1}^n f_i x_i}{\sum_{i=1}^n f_i}$

4. Median of Ungrouped Data If $n$ is odd :

   $\text { Median }=\left(\frac{n+1}{2}\right)^{t h} \text { observation }$
   If $\mathbf{n}$ is even :

   $\text { Median }=\frac{\text { Value of }\left(\frac{n}{2}\right)^{t h} \text { observation }+ \text { Value of }\left(\frac{n}{2}+1\right)^{t h} \text { observation }}{?}$

5. Median of Continuous Frequency Distribution: Median $=l+\frac{\left(\frac{N}{2}-c f\right)}{f} \times h$ where,
   l = lower limit of median class,
   N = number of observations,
   cf $=$ cumulative frequency of class preceding the median class,
   $\mathrm{f}=$ frequency of median class,
   $\mathrm{h}=$ class size (width) (assuming class size to be equal).

6. Mode $=l+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h$
   where
   $\mathrm{l}=$ lower limit of the modal class,
   $\mathrm{h}=$ size of the class interval (assuming all class sizes to be equal),
   $\mathrm{f}_1=$ frequency of the modal class,
   $\mathrm{f}_0=$ frequency of the class preceding the modal class,
   $f_2=$ frequency of the class succeeding the modal class.

7. Standard Deviation $\sigma=\sqrt{\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2}$

Also Read: JEE Main 2026 Important Formulas for Maths PDF

Also refer to JEE Main- Top 30 Most Repeated Questions & Topics

JEE Main 2026 Syllabus of Physics, Chemistry, Maths

The JEE Main 2026 syllabus for Physics, Chemistry, and Mathematics is based on the NCERT Class 11 and 12 curriculum. It covers key topics like Mechanics, Electricity, and Modern Physics in Physics, Physical, Organic, and Inorganic Chemistry in Chemistry, and Algebra, Calculus, and Coordinate Geometry in Maths. The syllabus aims to test conceptual understanding, application, and problem-solving skills. A thorough study of NCERT books along with mock tests and previous year papers is essential for scoring high. To know syllabus in detail you can through JEE Main 2026 Syllabus Page

Tips to Learn the Formula for JEE Main 2026

Students often find it challenging to learn formulas for the JEE Main, but with the right approach, they can effectively remember them. Given below are some points to remember:

1. Students must try to understand why a formula works. For example, derivations in Physics or Maths often follow a logical pattern.

2. Then break down formulas into chapters or topics.

3. To learn these formulas easily, try to make a formula notebook.

4. Sometimes students must try to make Mnemonics and short tricks, as it helps in quick revision.

5. Try to solve as many questions and revise

6. Try to use diagrams and flowcharts.