• Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • School
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
JEE Main Chemistry Formulas 2026 - Topic wise Important Formulas

JEE Main Chemistry Formulas 2026 - Topic wise Important Formulas

Ongoing Event

JEE Main Application Date:31 Oct' 25 - 27 Nov' 25

#JEE Main
Shivani PooniaUpdated on 02 Nov 2025, 02:25 PM IST

JEE Main Chemistry Formulas 2026 - The Joint Entrance Exam is one of the most competitive exam of engineering entrance exams. It is divided into three subsections (Physics, Chemistry, Maths). Chemistry is an important subject for JEE Main preparation. Hence, having a list of important formulas for JEE Main Chemistry 2025 is necessary. Every aspirant should have the short notes for JEE Mains that comprise the important formulas. These JEE important formulas for Chemistry help in solving the typical problems easily. Therefore, experts of Careers360 have issued a list of JEE Main 2026 Chemistry. The registration process for JEE Main 2026 is now open, and students can apply from 31 October 2025 to 27 November 2025. Session 1 of the exam will be conducted from 21 to 30 January 2026.

LiveJEE Main 2026 Registration LIVE: NTA JEE application form at jeemain.nta.nic.in; exam centres, patternNov 2, 2025 | 2:22 PM IST

India and federal government of Nigeria have partnered to establish an IIT in the West African country. IIT Nigeria campus will come up at Federal Government Academy in Suleja. 

Read More: India, Nigeria to set up IIT campus

Read More

This Story also Contains

  1. JEE Main 2026 Chemistry Formula Overview
  2. JEE Main Chemistry Important Formulas
  3. Preparation tips for JEE Mains
  4. How to Memorize Chemistry Formulas Effectively
JEE Main Chemistry Formulas 2026 - Topic wise Important Formulas
JEE Main Chemistry Formulas 2026

Download the JEE Main Chemistry Formulas E-Book below:
JEE Mains Chemistry all Formulas PDF Download

JEE Main 2026 Chemistry Formula Overview

There will be a total of 25 questions from Chemistry in JEE Main 2026, all of which have to be attempted. It is further segregated into Physical, Organic, and Inorganic sections. The maximum number of topics has been reduced from this section (chemistry) only. This makes Chemistry easier than before. However, the high-weightage topics for JEE Main remain the same.

Below are important formulas for JEE Main 2026 Chemistry that are helpful for both sessions. Candidates should solve as many Chemistry questions as they can and implement these formulas to remember them quickly. To crack the JEE Main exam with good marks, paste these formulas near the study table and memorise them.

UPES B.Tech Admissions 2026

Ranked #43 among Engineering colleges in India by NIRF | Highest Package 1.3 CR , 100% Placements

Apply
Jain University B.Tech Admissions 2026

100% Placement Record | Highest CTC 54 LPA | NAAC A++ Accredited | Ranked #62 in India by NIRF Ranking 2025 | JEE & JET Scores Accepted

Apply

JEE Main Chemistry Important Formulas

Candidates while studying chemistry, they need to revise and practice the chemical equations and symbols. To some, chemistry is a tough subject, but when candidates practice chemical equations, revise the properties, formulas and symbols, they will have command over the subject. Candidates can check the JEE Main Chemistry formulas below

JEE Main Important Formulas of Physical Chemistry

Some Basic Concepts in chemistry

  1. Boyle's Law: $P_1 V_1=P_2 V_2$ (at constant T and n )
  2. Charles's Law: $\frac{V_1}{T_1}=\frac{V_2}{T_2}($ at constant P and n$)$
  3. Avogadro's Law: $\frac{V}{n}=$ constant
  4. Average Atomic Mass $=\frac{\Sigma(\text { Mass of Isotopes })_i \times(\% \text { abundance })_i}{100}$
  5. Mole $=\frac{\mathrm{W}}{\mathrm{M}}=\frac{(\mathrm{Wt} . \text { of substance in gm. })}{(\text { Molar mass of substance }(\mathrm{G} . \mathrm{m} . \mathrm{m}))}$
  6. Mass $\%$ of an element $=\frac{\text { Mass of that element in one mole of the compound }}{\text { Molar mass of the compound }} \times 100$
  7. Equivalent Weight $=\frac{\text { Molecular weight }}{\mathrm{n}-\text { factor }(\mathrm{x})}$
JEE Main 2026: Preparation Tips & Study Plan
Download the JEE Main 2026 Preparation Tips PDF to boost your exam strategy. Get expert insights on managing study material, focusing on key topics and high-weightage chapters.
Download EBook

Atomic Structure

  1. Frequency $\nu=\frac{1}{\mathrm{~T}}$
  2. Wave number $(\bar{\nu})$ $\bar{\nu}=\frac{1}{\lambda}$
  3. $E=h \nu=\frac{h c}{\lambda}$

  4. Line Spectrum of Hydrogen-like atoms

    $\frac{1}{\lambda}=R Z^2\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)$

  5. Bohr radius of nth orbit:

    $\mathrm{r}_{\mathrm{n}}=0.529 \frac{\mathrm{n}^2}{\mathrm{Z}} \mathrm{~A}^0$

  6. Velocity of electron in nth orbit:

    $\mathrm{V}_{\mathrm{n}}=\left(2.18 \times 10^6\right) \frac{\mathrm{Z}}{\mathrm{n}} \mathrm{~m} / \mathrm{s}$

    where Z is atomic number

  7. Total energy of electron in nth orbit:

    $\mathrm{E}_{\mathrm{n}}=-13.6 \frac{\mathrm{Z}^2}{\mathrm{n}^2} \mathrm{eV}=-2.18 \times 10^{-18} \frac{\mathrm{Z}^2}{\mathrm{n}^2} \mathrm{~J}$

    where Z is atomic number

  8. Hisenberg Uncertainity Principle: $\Delta x . \Delta P \geq \frac{h}{4 \pi}$

  9. $\mathrm{E}_{\mathrm{n}}=-\frac{1312 \times \mathrm{Z}^2}{\mathrm{n}^2} \mathrm{~kJ} / \mathrm{mol}$

Lovely Professional University B.Tech Admissions 2026

India's Largest University | NAAC A++ | 100% Placements Record | Highest CTC 2.5 Cr PA | 150 + Programmes across Multiple Disciplines

Apply
Cambridge Institute of Technology B.Tech Admissions 2025

Highest CTC 53.5 LPA | Average CTC 7.2 LPA | 200+ Companies | 790+ Multiple offers

Apply

Chemical Thermodynamics

  1. Expansion Work $=\mathrm{P} \times \Delta \mathrm{V}=-\mathrm{P}_{\text {ext. }}\left[\mathrm{V}_2-\mathrm{V}_1\right]$
    $\mathrm{P}=$ external pressure And $\Delta \mathrm{V}=$ increase or decrease in volume.

  2. Work done in a reversible isothermal process

    $$
    \begin{aligned}
    & \mathrm{W}=-2.303 \mathrm{nRT} \log _{10} \frac{\mathrm{~V}_2}{\mathrm{~V}_1} \\
    & \mathrm{~W}=-2.303 \mathrm{nRT} \log _{10} \frac{\mathrm{P}_1}{\mathrm{P}_2}
    \end{aligned}
    $$

  3. Work done in an irreversible isothermal process
    Work $=-\mathrm{P}_{\text {ext. }}\left(\mathrm{V}_2-\mathrm{V}_1\right)$
    That is, Work $=-\mathrm{P} \times \Delta \mathrm{V}$

  4. $W=\Delta E=n C_V \Delta T$

  5. Enthalpy: $H=U+p V$

  6. First Law of Thermodynamics: $\Delta U=q+W$

  7. $\Delta \mathrm{G}=\Delta \mathrm{H}-\mathrm{T} \Delta(\mathrm{S})$

  8. $\Delta G=-n F E$

Equilibrium

  1. For a reaction:

    $\mathrm{mA}+\mathrm{nB} \rightleftharpoons \mathrm{pC}+\mathrm{qD}$ $\frac{\mathrm{K}_{\mathrm{f}}}{\mathrm{K}_{\mathrm{b}}}=\frac{[\mathrm{C}]^{\mathrm{p}}[\mathrm{D}]^{\mathrm{q}}}{[\mathrm{A}]^{\mathrm{m}}[\mathrm{B}]^{\mathrm{n}}}=\mathrm{K}_{\mathrm{c}}$

  2. $\mathrm{pH}=-\log _{10}\left[\mathrm{H}^{+}\right]$

  3. $\mathrm{k}_{\mathrm{w}}=\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right]=10^{-14}$

  4. $\mathrm{pH}=\mathrm{pK}_{\mathrm{a}}+\log _{10} \frac{[\text { Salt }]}{\text { Acid }}$

  5. $\mathrm{pOH}=\mathrm{pK}_{\mathrm{b}}+\log _{10} \frac{[\text { Salt }]}{[\text { Base }]}$

ELECTROCHEMISTRY

  1. $\mathrm{W}=\frac{\text { Eit }}{96500}$

  2. $\begin{aligned}
    & \frac{E_1}{E_2}=\frac{M_1}{M_2} \text { or } \frac{W_1}{W_2}=\frac{Z_1}{Z_2} \\
    & E_1=\text { equivalent weight } \\
    & E_2=\text { equivalent weight }
    \end{aligned}$
    W or M = mass deposited

  3. $\begin{aligned} & E_{\text {cell }} \text { or } E M F=\left[E_{\text {red }}(\text { cathode })-E_{\text {red }}(\text { anode })\right] \\ & E_{\text {eell }}^{\circ} \text { or } E M F^{\circ} \\ & =\left[E_{\text {red }}^{\circ}(\text { cathode })-E_{\text {red }}^{\circ}(\text { anode })\right]\end{aligned}$

  4. $\mathrm{E}=\mathrm{E}^{\circ}-\frac{\mathrm{RT}}{\mathrm{nF}} \ln Q$

  5. $\mathrm{xA}+\mathrm{yB} \xrightarrow{\mathrm{ne}^{-}} \mathrm{mC}+\mathrm{nD}$
    The emf can be calculated as

    $\text { Ecell }=\mathrm{E}^{\circ} \text { cell }-\frac{0.059}{\mathrm{n}} \log \frac{[\mathrm{C}]^{\mathrm{m}}[\mathrm{D}]^{\mathrm{n}}}{[\mathrm{~A}]^x[\mathrm{~B}]^{\mathrm{y}}}$

  6. $\wedge_{\mathrm{m}}=\kappa \times \frac{1000}{\mathrm{c}}$

  7. $\wedge_{\text {eq }}=\frac{1000 \times \kappa}{\mathrm{N}}$

Solutions

  1. Mass $\%$ of a component $=\frac{\text { Mass of the component in the solution }}{\text { Total mass of the solution }} \times 100$
  2. Volume $\%$ of a component $=\frac{\text { Volume of the component }}{\text { Total volume of solution }} \times 100$
  3. Mass by Volume $\%$ of a component $=\frac{\text { Mass of the component }}{\text { Total volume of solution }} \times 100$
  4. Parts per million $=\frac{\text { Number of parts of the component }}{\text { Total number of parts of all components of the solution }} \times 10^6$
  5. Mole fraction of a component $=\frac{\text { Number of moles of the component }}{\text { Total number of moles of all the components }}$
  6. Molarity: $(M)=\frac{\text { No. of Moles of Solutes }}{\text { Volume of Solution in Liters }}$
  7. Molality: $(m)=\frac{\text { No. of Moles of Solutes }}{\text { Mass of solvent in } \mathrm{kg}}$
  8. $\left(P_T\right)=P_A^o X_A+P_B^o X_B$ ($\begin{aligned} & P_A=P_A^o X_A \\ & P_B=P_B^o X_B \\ & P_T=P_A+P_B\end{aligned}$)
  9. $\Delta \mathrm{T}_{\mathrm{b}}=\mathrm{K}_{\mathrm{b}} \times \frac{\mathrm{w}}{\mathrm{M}} \times \frac{1000}{\mathrm{~W}}$
  10. $\Delta T_f=K_f \times \frac{w}{M} \times \frac{1000}{W}$
  11. $\Pi=C R T$
  12. $\begin{aligned} & \mathrm{i}=\frac{\text { Observed number of solute particles }}{\text { Number of particles initially taken }} \\ & \mathrm{i}=\frac{\text { Observed value of colligative property }}{\text { Theoretical value of colligative property }}\end{aligned}$

Chemical kinetics

  1. Unit of average velocity $=\frac{\text { Unit of concentration }}{\text { Unit of time }}=\frac{\text { mole }}{\text { litre second }}=$ mole litre $^{-1}$ second $^{-1}$
  2. $\mathrm{aA}+\mathrm{bB} \rightarrow \mathrm{cC}+\mathrm{dD}$
    Rate w.r.t. $[\mathrm{A}]=-\frac{\mathrm{d}[\mathrm{A}]}{\mathrm{dt}} \times \frac{1}{\mathrm{a}}$
    Rate w.r.t. $[B]=-\frac{d[B]}{d t} \times \frac{1}{b}$
    Rate w.r.t. $[\mathrm{C}]=-\frac{\mathrm{d}[\mathrm{C}]}{\mathrm{dt}} \times \frac{1}{\mathrm{c}}$
    Rate w.r.t. $[\mathrm{D}]=-\frac{\mathrm{d}[\mathrm{D}]}{\mathrm{dt}} \times \frac{1}{\mathrm{~d}}$
  3. $\mathrm{R} \propto[\mathrm{A}]^{\mathrm{p}}[\mathrm{B}]^{\mathrm{q}}$

  4. Unit of Rate Constant-

    $\begin{aligned}
    & \text { The differential rate expression for } \mathrm{n}^{\text {th }} \text { order reaction is as follows: } \\
    & \qquad-\frac{\mathrm{dx}}{\mathrm{dt}}=\mathrm{k}(\mathrm{a}-\mathrm{x})^{\mathrm{n}} \\
    & \text { or } \quad \mathrm{k}=\frac{\mathrm{dx}}{(\mathrm{a}-\mathrm{x})^{\mathrm{n}} \mathrm{dt}}=\frac{(\text { concentration })}{(\text { concentration })^{\mathrm{n}} \text { time }}=(\text { conc. })^{1-\mathrm{n}} \text { time }^{-1}
    \end{aligned}$

  5. For the first-order reaction,

    $k=\frac{2.303}{t} \log \frac{[\mathrm{R}]_0}{[\mathrm{R}]}$

  6. $t_{1 / 2}=\frac{0.693}{k}$

  7. For any general nth order reaction it is evident that,

    $\mathrm{t}_{\frac{1}{2}} \propto[\mathrm{~A}]_0^{1-\mathrm{n}}$
    It is to be noted that the above formula is applicable for any general nth-order reaction except $\mathrm{n}=1$.

  8. Arrhenius Equation: $\mathrm{k}=\mathrm{Ae}^{-\mathrm{Ea} / \mathrm{RT}}$

  9. $\log \frac{\mathrm{K}_2}{\mathrm{~K}_1}=\frac{\mathrm{Ea}}{2.303 \mathrm{R}}\left[\frac{1}{\mathrm{~T}_1}-\frac{1}{\mathrm{~T}_2}\right]$

JEE Main Important Formulas of Inorganic Chemistry

Coordination Compounds

  1. $\mathrm{EAN}=Z-O+2 L$
    Where:
    $\mathbf{Z}=$ Atomic number of the central metal atom/ion
    $\mathbf{O}=$ Oxidation state of the metal atom/ion
    L = Number of ligands (or donor atoms) $\times$ number of electrons donated per ligand

  2. Crystal Field Stabilization Energy (CFSE):
    Octahedral:

    $$
    \mathrm{CFSE}=(-0.4 x+0.6 y) \Delta_0
    $$

    Tetrahedral:

    $$
    \mathrm{CFSE}=(-0.6 x+0.4 y) \Delta_t
    $$

    where $x=t_2 g$ electrons, $y=$ e_g electrons

d- & f-Block Elements

  1. Magnetic Moment:

    $\mu=\sqrt{n(n+2)} \mathrm{BM}$

Chemical Bonding and Molecular Structure

  1. Formal Charge:

    $\text { F.C. }=V-N-\frac{B}{2}$

    ( $\mathrm{V}=$ valence electrons, $\mathrm{N}=$ non-bonding, $\mathrm{B}=$ bonding electrons)

  2. Bond Order (Molecular Orbital Theory):

    $\text { Bond Order }=\frac{\left(N_b-N_a\right)}{2}$

  3. Dipole Moment:

    $\mu=q \times d$

    ( $q=$ charge,$d=$ distance between charges)

JEE Main Important Formulas: Inorganic Chemistry

Some Basic Principles of Organic Chemistry

  1. Application of Inductive Effect

    The decreasing -I effect or increasing +I effect order is as follows:

    $\begin{aligned}
    & -\mathrm{NH}_3+>-\mathrm{NO}_2>-\mathrm{SO}_2 \mathrm{R}>-\mathrm{CN}>-\mathrm{SO}_3 \mathrm{H}>-\mathrm{CHO}>-\mathrm{CO}>-\mathrm{COOH}>-\mathrm{F}>-\mathrm{COCl}>-\mathrm{CONH}_2>-\mathrm{Cl}>-\mathrm{Br}>-\mathrm{I}>-\mathrm{OR}>-\mathrm{OH}>-\mathrm{NR}_2>-\mathrm{NH}_2> \\
    & -\mathrm{C}_6 \mathrm{H}_5>-\mathrm{CH}=\mathrm{CH}_2>-\mathrm{H}
    \end{aligned}$

  2. Degree of Unsaturation (DU or IHD):

    $\mathrm{DU}=\frac{2 C+2-H+N-X}{2}$

    ( $\mathrm{C}=$ carbon, $\mathrm{H}=$ hydrogen, $\mathrm{N}=$ nitrogen, $\mathrm{X}=$ halogen)

Hydrocarbons

  1. Alkanes: $C_n H_{2 n+2}$
  2. Alkenes: $C_n H_{2 n}$
  3. Alkynes: $C_n H_{2 n-2}$

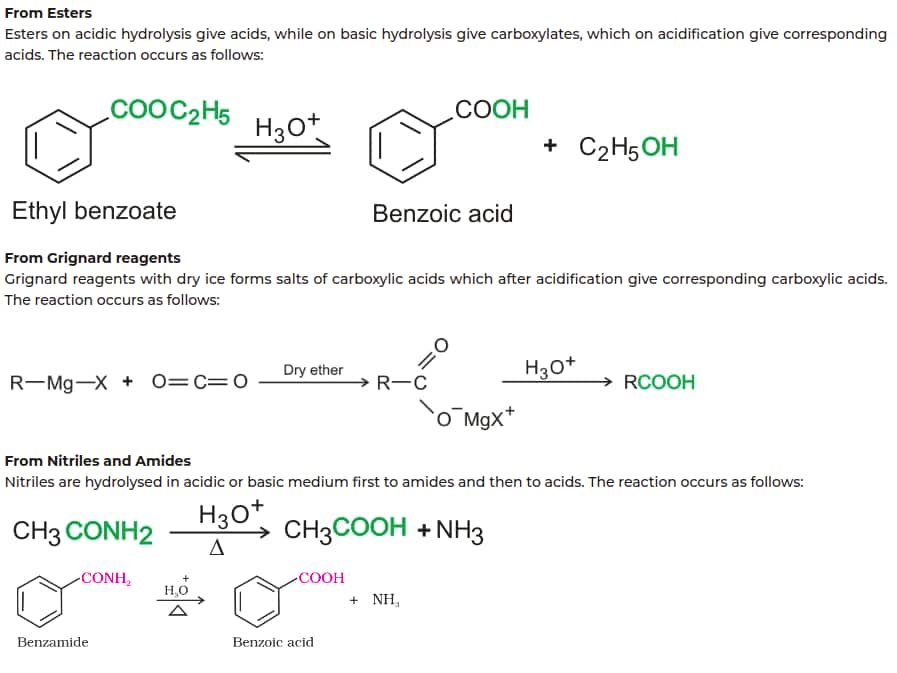
Carboxylic Acids and Derivatives

Method of Preparation of Carboxylic Acid

1701851769429

Preparation tips for JEE Mains

Given below are some tips to help you prepare for JEE Main and score good marks in the exam:

1. First, students need to understand the Syllabus and Exam Pattern so that they can refer to the JEE Main syllabus from the official website.

2. Try to identify the important and high-weightage topics and prepare according to that.

3. Create an effective study plan according to your preparation level. Divide your preparation into monthly, weekly, and daily targets and allocate more time to difficult subjects or topics.

4. Students must focus on conceptual clarity; they must understand the logic and derivations behind every formula.

5. Try to solve questions regularly. Solve previous years' JEE Main question papers and attempt mock tests and sample papers regularly.

Recommended eBooks

Related eBooks & Sample Papers

JEE Main 2026 Paper 2 (B.Arch) Syllabus

1793+ Downloads

JEE Main 2026 Math Syllabus

9665+ Downloads

How to Memorize Chemistry Formulas Effectively

Students find it difficult to learn formulas for JEE Main, but with the right approach, they can remember them. Given below are some points to remember:

1. Students must try to understand why a formula works and how chemical reactions occur, and their mechanism.

2. Then break down formulas into chapters or topics.

3. To learn these formulas easily, try to make a formula notebook.

4. Sometimes students must try to make Mnemonics and short tricks, as it helps in quick revision.

5. Try to solve as many questions and revise

6. Try to use diagrams and flowcharts.

JEE Main Syllabus: Subjects & Chapters
Select your preferred subject to view the chapters

Frequently Asked Questions (FAQs)

Q: What is the JEE Mains ?
A:

JEE Main is an exam conducted for those aspirants who want to take admission in NIITs, IITs and other engineering colleges, and it is also an eligibility test for JEE advance.

Q: Which part of chemistry has many formulas ?
A:

Chemistry has three subparts (Physical, inorganic and organic). Physical chemistry has many numericals based on different formulas.

Q: Is the class 12 syllabus important for the JEE Main Exam ?
A:

Yes, Class 12 syllabus carries more than 50% of weightage, so it is important for JEE Main Exam.

Articles
Related Stories
|
Upcoming Engineering Exams
KL University Engineering Entrance Examination
Ongoing Dates
KLEEE Application Date

18 Sep'25 - 12 Nov'25 (Online)

Certifications By Top Providers
Basic Programming using Python
Via Indian Institute of Technology Bombay
Introduction to Aerospace Engineering
Via Indian Institute of Technology Bombay
Fundamental Concepts of Electricity
Via Indian Institute of Technology Bombay
Artificial Intelligence
Via Columbia University, New York
Computer Fundamentals
Via Devi Ahilya Vishwavidyalaya, Indore
B.Sc in Programming and Data Science
Via Indian Institute of Technology Madras
Udemy
 1525 courses
Swayam
 817 courses
NPTEL
 773 courses
Coursera
 697 courses
Edx
 608 courses
Explore Top Universities Across Globe
Georgia Institute of Technology, Atlanta
North Avenue, Atlanta, Georgia 30332
University of Nottingham, Nottingham
University Park, Nottingham NG7 2RD
Texas A and M University, College Station
400 Bizzell St College Station, Texas 77843
University College London, London
Gower Street, London, WC1E 6BT
Michigan Technological University, Houghton
1400 Townsend Drive, Houghton, Michigan 49931-1295
University of Strathclyde, Glasgow
16 Richmond St, Glasgow G1 1XQ

Popular Courses and Specializations

Popular Degrees

Popular Branches

List of colleges accepting JEE Main

Questions related to JEE Main

On Question asked by student community

Have a question related to JEE Main ?
Jee main registration is live but I don't know if I have an option of choosing exam centre. Because I live in kota for prep but my hometown is in Bihar. And admit card is released just before the exams, it will be tough for me to catch.

Hello,

Yes, during JEE Main registration, you can choose up to four preferred exam cities in order of priority. Since you are staying in Kota but belong to Bihar, you can select both locations. For example, Kota as your first choice and your hometown city in Bihar as another option.
When the admit card is released (usually a week before the exam), the final center will be allotted from your chosen options.


Hope you understand.

Read Complete Answer
S
Sankalp Agrawal
1 Nov'25
jee mains paper 2A cut off 2025

Hello Devanshi

To know the Cutoff of the JEE Mains exam paper for the year 2025, and for previous year, you can visit the link I am attaching below. The link will provide you with the data and help you to improve your performance.

https://engineering.careers360.com/articles/jee-main-cutoff-for-b-arch-b-planning

Read Complete Answer
S
SEJAL JAIN
31 Oct'25
Niper JEE 2021 Previous Year Question Available?

Hello dear candidate,

Here is the link of NIPER JEE previous year questions along with their solutions, it has question papers with solutions for year 2019-2025, including your requirement of 2021 :-

https://pharmacy.careers360.com/download/ebooks/niper-jee-previous-year-question-paper-pdf

I hope you find this helpful. Thank you.

Read Complete Answer
A
Amisha Soni
31 Oct'25
I am reappearing in 12th cbse exams 2026 as I had a compartment in over-all result. I have to fill for jee mains and advanced in 2026, but now NTA requires 11th registration number, so will it hamper my enrollment in mains? Will NTA consider me a 12th grader or a dropper? Please explain in detail.

Hello dear candidate,

You can fill your JEE main and advance forms 2026 normally . No, your 11th registration number will not cause any problem.

You will be treated as 12th appearing student in 2026, not as a dropper . You just need to make sure that your CBSE 12th result comes out in 2026 before counselling.

Thank you.

Read Complete Answer
A
Amisha Soni
31 Oct'25
I have done my 10th and 12th in punjab but my both parents are from himachal. Next year is jee, can I still apply for himachal state quota? or am I only eligible for punjab domicile?

To be eligible for Himachal Pradesh state quota you must have passed atleast two examinations from Himachal pradesh including the 10th and 12th grades. The other criteria are for government employee wards, if the parents have worked there for atleast two years and completed their 10th and 12th from HP.

Read Complete Answer
A
Aadesh Sharma
31 Oct'25
View all

Popular JEE Main Questions

Are previous year questions repeated in JEE Mains?
Read Complete Answer
How to crack JEE Main in 1st attempt?
Read Complete Answer
When will JEE Main admit card come?
Read Complete Answer
How to check JEE Main Exam Centre?
Read Complete Answer
How to check JEE Main Result?
Read Complete Answer
How to make jee main admit card correction?
Read Complete Answer
How to download jee main admit card?
Read Complete Answer
How to download JEE Main admit card without password?
Read Complete Answer
What not to carry to JEE Main exam hall?
Read Complete Answer
What to carry to the exam hall of JEE Main 2018?
Read Complete Answer

Study Resources, Applications and Opportunities

Lovely Professional University B.Tech Admissions 2026
Apply

India's Largest University | NAAC A++ | 100% Placements Record | Highest CTC 2.5 Cr PA | 150 + Programmes across Multiple Disciplines

UPES B.Tech Admissions 2026
Apply

Ranked #43 among Engineering colleges in India by NIRF | Highest Package 1.3 CR , 100% Placements

New Horizon College of Engineering B.E. Admissions 2025
Apply

AICTE ‘Platinum’ institute | NIRF 2024 Rank Band 151-200 under the engineering category | Tier-1 accreditation by NBA | Merit & Sports Scholarships

IITs- A Complete Guide
Get now

Dive into everything you need to know about IITs—from eligibility and cutoffs to fees and placements.

Atlas SkillTech University | B.Tech Admissions
Apply

Hands on Mentoring and Code Coaching | Cutting Edge Curriculum with Real World Application

Pimpri Chinchwad University B.Tech Admissions
Apply

1000+ Recruiters | 450+ Patents | 50000+ Alumni network

View all Application Forms

JEE Main Notifications

Latest updates

Explore Career Options

By Industry
Flight Attendant

A flight attendant ensures passenger safety and comfort during flights. Key duties include conducting safety checks, assisting passengers, serving food and drinks, and managing emergencies. They must be well-trained in safety procedures and customer service. A high school diploma is typically required, followed by rigorous training to qualify for the role.

3 Jobs Available
Flight Engineer

A Flight Engineer monitors and operates an aircraft’s complex systems like engines, fuel, and hydraulics during flight, ensuring optimal performance and safety. They assist pilots with technical issues, conduct inspections, and maintain records. This role requires strong technical knowledge, problem-solving, and communication skills. Training usually involves a degree in aviation or aerospace engineering and specialised certification.

2 Jobs Available
Aircrew officer

An Aircrew Officer operates and navigates aircraft, ensuring safe flights and compliance with aviation regulations. Key duties include managing flight systems, conducting pre- and post-flight checks, and adhering to safety standards. The role typically requires working five days a week, with around 120 flight hours monthly. Employment may be contractual or permanent, depending on the airline.

2 Jobs Available
Aerospace Engineer

An aerospace engineer designs, develops, tests, and maintains aircraft, spacecraft, and related systems. They apply physics and engineering principles to improve aerospace technologies, often working in aviation, defence, or space sectors. Key tasks include designing components, conducting tests, and performing research. A bachelor’s degree is essential, with higher roles requiring advanced study. The role demands analytical skills, technical knowledge, precision, and effective communication.

2 Jobs Available
Air Hostess

An air hostess, or flight attendant, ensures passenger safety and comfort during flights. Responsibilities include safety demonstrations, serving meals, managing the cabin, handling emergencies, and post-flight reporting. The role demands strong communication skills, a calm demeanour, and a service-oriented attitude. It offers opportunities to travel and work in the dynamic aviation and hospitality industry.

2 Jobs Available
Aeronautical Engineer

An aeronautical engineer designs, develops, tests, and maintains aircraft and related systems. They work on components like engines and wings, ensuring performance, safety, and efficiency. The role involves simulations, flight testing, research, and technological innovation to improve fuel efficiency and reduce noise. Aeronautical engineers collaborate with teams in aerospace companies, government agencies, or research institutions, requiring strong skills in physics, mathematics, and engineering principles.

2 Jobs Available
Safety Manager

A Safety Manager ensures workplace safety by developing policies, conducting training, assessing risks, and ensuring regulatory compliance. They investigate incidents, manage workers’ compensation, and handle emergency responses. Working across industries like construction and healthcare, they combine leadership, communication, and problem-solving skills to protect employees and maintain safe environments.

2 Jobs Available
Airline Pilot

An airline pilot operates aircraft to transport passengers and cargo safely. Responsibilities include pre-flight planning, in-flight operations, team collaboration, and post-flight duties. Pilots work in varying schedules and environments, often with overnight layovers. The demand for airline pilots is expected to grow, driven by retirements and industry expansion. The role requires specialized training and adaptability.

1 Jobs Available

Never miss an JEE Main update

Get timely JEE Main updates directly to your inbox. Stay informed!