Amity University-Noida B.Tech Admissions 2026
Among top 100 Universities Globally in the Times Higher Education (THE) Interdisciplinary Science Rankings 2026
Getting 250+ marks in JEE Main isn't just about studying everything, it also includes studying wisely. One of the smartest study techniques is to perfectly master the JEE Main repeated questions all subjects that can be asked. For the last 15 years or so, JEE Main exam has appeared to follow a very distinct repetition pattern across Physics, Chemistry, and Mathematics; that is, concepts are asked again and again with slight numerical or conceptual changes.
This Story also Contains

This article focuses on the Top 25 Repeated JEE Mains Questions that have been appearing consistently in previous years and have a critical role in scoring above 250 marks.
To score 250+ marks in JEE Main 2026, focusing on JEE Main PYQs is important and the chapters that carry high weightage and are frequently repeated in the exam. These chapters afford the maximum possible marks with minimum investment of time and rely heavily on the question patterns from previous years.
|
Chapter Name |
Percentage Distribution |
|
Co-ordinate geometry |
13.11% |
|
Integral Calculus |
10.43% |
|
Limit, continuity and differentiability |
10.28% |
|
Complex numbers and quadratic equations |
7.04% |
|
Matrices and Determinants |
7.04% |
| Three Dimensional Geometry | 6.91% |
|
Chapter Name |
Percentage Distribution |
|
Optics |
7.54% |
|
Properties of Solids and Liquids |
7.01% |
|
Electrostatics |
7.41% |
|
Current Electricity |
6.85% |
|
Electromagnetic Induction and Alternating Currents |
6.23% |
| Magnetic Effects of Current and Magnetism | 5.86% |
|
Chapter Name |
Percentage Distribution |
|
Organic Compounds containing Oxygen |
6.85% |
|
Co-ordination Compounds |
5.92% |
|
p- Block Elements |
5.30% |
|
Redox Reaction and Electrochemistry |
5.27% |
|
Hydrocarbons |
5.21% |
| Chemical Bonding and Molecular Structure | 4.69% |
|
Concept Name |
Total Number of Questions from last five years |
|
De-broglie wavelength of an electron |
38 |
|
Logic Gates |
36 |
|
Parallel Grouping of Resistance |
33 |
|
Projectile Motion |
33 |
| Nature of Electromagnetic Waves | 31 |
| Hooke’s law | 29 |
|
Concept Name |
Total Number of Questions from last five years |
|
Concentration Terms |
30 |
|
Mole Concept and Molar Mass |
27 |
|
Stoichiometry, Stoichiometric Calculations and Limiting Reagent |
25 |
|
Applications of CFT |
25 |
| Magnetic Moment (On the Basis of VBT) | 24 |
|
Concept Name |
Total Number of Questions from last five years |
|
Linear Differential Equation |
79 |
|
Area Bounded by Two Curves |
73 |
|
Dispersion (Variance and Standard Deviation) |
60 |
|
Vector (or Cross) Product of Two Vectors |
54 |
|
General Term of Binomial Expansion |
45 |
| Definite Integration | 44 |
Question 1: Let the Mean and Variance of five observations $x_1=1, x_2=3, x_3=a, x_4=7$ and $x_5=b, a>b$, be 5 and 10, respectively. Then the Variance of the observations $n+x_n, n=1,2, \ldots \ldots . .5$ is
1) 17
2) 16.4
3) 17.4
4) (correct) 16
Solution:
Calculate the mean:
$\begin{aligned}
& 5=\frac{1+3+a+7+b}{5} \\
& \Rightarrow a+b=14 \\
& \frac{1+9+a^2+49-b^2}{5}-(5)^2=10 \\
& a^2+b^2=116 \\
& \Rightarrow a=10, b=4
\end{aligned}$
New observations: $2,5,13,11,9$
$\begin{aligned}
& \text { Var }=\frac{4+26+169+121+81}{5}-64 \\
& \text { Var }=80.2-64 \\
& \text { Var } \approx 16
\end{aligned}$
Hence, the answer is option (4).
Question 2: If in the expansion of $(1+x)^p(1-x)^q$, the coefficients of $x$ and $x^2$ are 1 and -2 , respectively, then $\mathbf{p}^2+\mathbf{q}^2$ is equal to:
1) 8
2) 18
3) (correct) 13
4) 20
Solution:
We have:
$
(1+x)^p(1-x)^q = \left({}^p C_0 + {}^p C_1 x + {}^p C_2 x^2 + \ldots\right)\left({}^q C_0 - {}^q C_1 x + {}^q C_2 x^2 - \ldots\right)
$
To find the coefficient of $x$, we consider terms whose degrees add up to 1:
Coefficient of $x = {}^p C_0 \cdot ( - {}^q C_1 ) + {}^p C_1 \cdot {}^q C_0 = -{}^q C_1 + {}^p C_1 = 1
$
Given that $p - q = 1$, so:
$
p = q + 1
$
Now for the coefficient of $x^2$, the relevant terms are:
Coefficient of $x^2 = {}^p C_0 \cdot {}^q C_2 - {}^p C_1 \cdot {}^q C_1 + {}^p C_2 \cdot {}^q C_0 = -2
$
Now express binomial coefficients using formulas:
$
{}^q C_2 = \frac{q(q - 1)}{2}, \quad {}^p C_2 = \frac{p(p - 1)}{2}, \quad {}^p C_1 = p, \quad {}^q C_1 = q
$
Substitute these into the expression:
$
\frac{q(q - 1)}{2} - pq + \frac{p(p - 1)}{2} = -2
$
Multiply the entire equation by 2 to eliminate denominators:
$
q(q - 1) - 2pq + p(p - 1) = -4
$
Simplify:
$
q^2 - q - 2pq + p^2 - p = -4
$
Now substitute $p = q + 1$ into the equation:
$
q^2 - q - 2q(q + 1) + (q + 1)^2 - (q + 1) = -4
$
Expand:
$
q^2 - q - 2q^2 - 2q + q^2 + 2q + 1 - q - 1 = -4
$
Simplify:
$
(q^2 - 2q^2 + q^2) + (-q - 2q + 2q - q) + (1 - 1) = -4
\Rightarrow 0 - 2q = -4 \Rightarrow q = 2
$
Now:
$
p = q + 1 = 3
$
Therefore:
$
p^2 + q^2 = 3^2 + 2^2 = 9 + 4 = 13
$
Hence, the correct answer is option (3).
Question 3: A box contains 10 pens, of which 3 are defective. A sample of 2 pens is drawn at random, and let $X$ denote the number of defective pens. Then the variance of $X$ is
1) $\frac{11}{15}$
2) (correct) $\frac{28}{75}$
3) $\frac{2}{15}$
4) $\frac{3}{5}$
Solution:
| x | x = 0 | x = 1 | x = 2 |
| $\mathrm{P}(\mathrm{x})$ | $\frac{{ }^7 \mathrm{C}_2}{{{ }^{10} \mathrm{C}_2}}$ | $\frac{{ }^{7} \mathrm{C}_1 \ ^{3}C_1 }{^{10} \mathrm{C}_2}$ | $\frac{{ }^3 \mathrm{C}_2}{{ }^{10} \mathrm{C}_2}$ |
Among top 100 Universities Globally in the Times Higher Education (THE) Interdisciplinary Science Rankings 2026
Last Date to Apply: 26th March | Ranked #43 among Engineering colleges in India by NIRF | Highest Package 1.3 CR , 100% Placements
$\begin{aligned} & \mu=\Sigma x_i P\left(x_i\right)=0+\frac{7}{15}+\frac{2}{15}=\frac{3}{5} \\ & \text { Variance }(x)=\Sigma P_i\left(x_i-\mu\right)^2=\frac{28}{75}\end{aligned}$
Hence, the correct answer is option (2).
Question 4: If the area of the larger portion bounded between the curves $x^2+y^2=25$ and $y=|x-1|$ is $\frac{1}{4}(b \pi+c), \mathrm{b}, \mathrm{c} \in \mathbb{N}$, then $\mathrm{b}+\mathrm{c}$ is equal to $\_\_\_\_$ .
Solution :
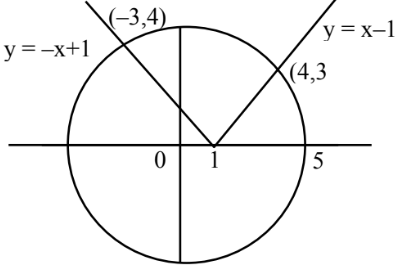
Given the circles:
$
x^2 + y^2 = 5
$
and
$
x^2 + (x-1)^2 = 25
$
Solve for $x$ in the second equation:
$
x^2 + (x-1)^2 = 25 \implies x=4
$
Also, from the first circle and $y = -x + 1$,
$
x^2 + (-x + 1)^2 = 5 \implies x = -3
$
Calculate the required area $A$:
$
A = 25 \pi - \int_{-3}^{4} \sqrt{25 - x^2} \, dx + \frac{1}{2} \times 4 \times 4 + \frac{1}{2} \times 3 \times 3
$
Evaluate the integral:
$
A = 25 \pi + \frac{25}{2} - \left[ \frac{x}{2} \sqrt{25 - x^2} + \frac{25}{2} \sin^{-1} \frac{x}{5} \right]_{-3}^{4}
$
Calculate the terms inside the bracket:
$
A = 25 \pi + \frac{25}{2} - \left[ 6 + \frac{25}{2} \sin^{-1} \frac{4}{5} + 6 + \frac{25}{2} \sin^{-1} \frac{3}{5} \right]
$
Simplify the expression:
$
A = 25 \pi + \frac{1}{2} - \frac{25}{2} \cdot \frac{\pi}{2}
$
Further simplification yields:
$
A = \frac{75 \pi}{4} + \frac{1}{2}
$
Rewrite as:
$
A = \frac{1}{4} (75 \pi + 2)
$
Identify $b=75$ and $c=2$, then
$
b + c = 75 + 2 = 77
$
Hence, the answer is 77.
Question 5: Let $y=y(x)$ be the solution of the differential equation $\left(x y-5 x^2 \sqrt{1+x^2}\right) d x+\left(1+x^2\right) d y=0, y(0)=0$. Then $y(\sqrt{3})$ is equal to
1) (correct) $\frac{5 \sqrt{3}}{2}$
2) $\sqrt{\frac{14}{3}}$
3) $2 \sqrt{2}$
4) $\sqrt{\frac{15}{2}}$
Solution:
We are given:
$
(1 + x^2) \frac{dy}{dx} + x y = 5x^2 \sqrt{1 + x^2}
$
Divide both sides by $ 1 + x^2 $:
$
\frac{dy}{dx} + \frac{x}{1 + x^2} y = \frac{5x^2}{\sqrt{1 + x^2}}
$
This is a linear differential equation. The integrating factor is:
$
\text{I.F.} = e^{\int \frac{x}{1 + x^2} dx} = e^{\frac{1}{2} \ln(1 + x^2)} = \sqrt{1 + x^2}
$
Multiply both sides of the differential equation by the I.F.:
$
\sqrt{1 + x^2} \cdot \frac{dy}{dx} + \frac{x \sqrt{1 + x^2}}{1 + x^2} y = \frac{5x^2}{\sqrt{1 + x^2}} \cdot \sqrt{1 + x^2}
$
Left-hand side becomes:
$
\frac{d}{dx} \left( y \sqrt{1 + x^2} \right) = 5x^2
$
Integrate both sides:
$
y \sqrt{1 + x^2} = \int 5x^2 dx = \frac{5x^3}{3} + C
$
Use initial condition $ y(0) = 0 $:
$
0 = \frac{5 \cdot 0^3}{3 \cdot \sqrt{1 + 0^2}} + C \Rightarrow C = 0
$
So,
$
y = \frac{5x^3}{3 \sqrt{1 + x^2}}
$
Now evaluate $ y(\sqrt{3}) $:
$
y(\sqrt{3}) = \frac{5 (\sqrt{3})^3}{3 \sqrt{1 + 3}} = \frac{5 \cdot 3 \sqrt{3}}{3 \cdot 2} = \frac{5 \sqrt{3}}{2}
$
$
y(\sqrt{3}) = \frac{5 \sqrt{3}}{2}
$
Hence, the answer is Option (1).
Question 6: If for the solution curve $y=f(x)$ of the differential equation $\frac{d y}{d x}+(\tan x) y=\frac{2+\sec x}{(1+2 \sec x)^2}$, $\mathbf{x} \in\left(\frac{-\pi}{2}, \frac{\pi}{2}\right), \mathrm{f}\left(\frac{\pi}{3}\right)=\frac{\sqrt{3}}{10}$, then $\mathrm{f}\left(\frac{\pi}{4}\right)$ is equal to:
1) $\frac{9 \sqrt{3}+3}{10(4+\sqrt{3})}$
2) $\frac{\sqrt{3}+1}{10(4+\sqrt{3})}$
3) $\frac{5-\sqrt{3}}{2 \sqrt{2}}$
4) (correct) $\frac{4-\sqrt{2}}{14}$
Solution:
Linear Differential Equation -
The linear differential equations are those in which the variable and its derivative occur only in the first degree.
An equation of the form
$
\frac{d y}{d x}+P(x) \cdot y=Q(x)
$
Where P(x) and Q(x) are functions of x only or constant is called a linear equation of the first order.
$
\Rightarrow \quad \mathrm{ye}^{\int P(x) d x}=\int Q(x) e^{\int P(x) d x} d x+C
$
Which is the required solution to the given differential equation.
The term $\mathrm{e}^{\int \mathrm{P}(\mathrm{x}) \mathrm{dx}}$, which converts the left-hand expression of the equation into a perfect differential, is called an Integrating factor (IF).
Thus, we remember the solution of the above equation as
$
y(\mathrm{IF})=\int Q(\mathrm{IF}) d x+C
$
Question 7: The magnetic field of an E.M. wave is given by
$\overrightarrow{\mathrm{B}}=\left(\frac{\sqrt{3}}{2} \hat{\mathrm{i}}+\frac{1}{2} \hat{\mathrm{j}}\right) 30 \sin \left[\omega\left(\mathrm{t}-\frac{\mathrm{z}}{\mathrm{c}}\right)\right] \text { (S.I. Units) }$
The corresponding electric field in SI units is :
1) $\overrightarrow{\mathrm{E}}=\left(\frac{1}{2} \hat{\mathrm{i}}-\frac{\sqrt{3}}{2} \hat{\mathrm{j}}\right) 30 \mathrm{c} \sin \left[\omega\left(\mathrm{t}-\frac{\mathrm{z}}{\mathrm{c}}\right)\right]$
2) $\overrightarrow{\mathrm{E}}=\left(\frac{3}{4} \hat{\mathrm{i}}+\frac{1}{4} \hat{\mathrm{j}}\right) 30 \mathrm{c} \cos \left[\omega\left(\mathrm{t}-\frac{\mathrm{z}}{\mathrm{c}}\right)\right]$
3) $\overrightarrow{\mathrm{E}}=\left(\frac{1}{2} \hat{\mathrm{i}}+\frac{\sqrt{3}}{2} \hat{\mathrm{j}}\right) 30 \mathrm{c} \sin \left[\omega\left(\mathrm{t}+\frac{\mathrm{z}}{\mathrm{c}}\right)\right]$
4) $\overrightarrow{\mathrm{E}}=\left(\frac{\sqrt{3}}{2} \hat{\mathrm{i}}-\frac{1}{2} \hat{\mathrm{j}}\right) 30 \mathrm{c} \sin \left[\omega\left(\mathrm{t}+\frac{\mathrm{z}}{\mathrm{c}}\right)\right]$
Solution:
$\begin{aligned} & \vec{B}=\left(\frac{\sqrt{3}}{2} \hat{i}+\frac{1}{2} \hat{j}\right) 30 \sin \left[\omega\left(t-\frac{z}{c}\right)\right] \\ & \vec{E}=\vec{B} \times \overrightarrow{\mathrm{c}} \text { and } E_0 = B_0 c \\ & \hat{E} = \left(\frac{\sqrt{3}}{2}(-\hat{j})+\frac{1}{2} \hat{i}\right) \\ & E_0=30 c \\ & \vec{E}=\left(\frac{1}{2} \hat{i}-\frac{\sqrt{3}}{2} \hat{j}\right) 30 c \sin \left[\omega\left(t-\frac{z}{c}\right)\right]\end{aligned}$
Hence, the answer is the option (1).
Question 8: Xg of nitrobenzene on nitration gave 4.2 g of m -dinitrobenzene. $\mathrm{X}=$ $\_\_\_\_$ g. (nearest integer)
[Given : molar mass (in gmol $^{-1}$ ) $\mathrm{C}: 12, \mathrm{H}: 1, \mathrm{O}: 16, \mathrm{~N}: 14$ ]
Solution:
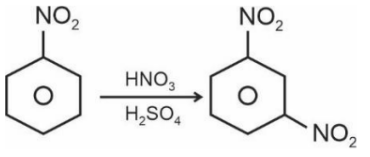
Given
X g nitrobenzene
4.2 g m -dinitrobenzene.
MM of nitrobenzene = 123
MM of dinitrobenzene = 168
$\begin{aligned} & \frac{X}{123}=\frac{4.2}{168} \\ & X=3.075 \mathrm{~g}\end{aligned}$
Hence, the answer is 3.075
Question 9: The homoleptic and octahedral complex of $\mathrm{Co}^{+2}$ and $\mathrm{H}_2 \mathrm{O}$ has $\_\_\_\_$ unparied electrons(s) in the $t_{2 g}$ set of orbitals.
Solution:
$\left(\mathrm{Co}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right)^{+2} \rightarrow \mathrm{CO}^{+2} \rightarrow 3 \mathrm{~d}^7$
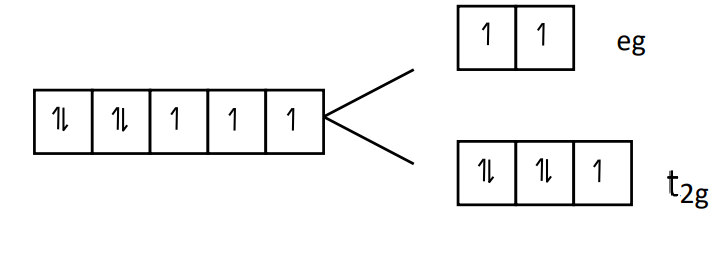
unpaired electrons in $t_{2 g}$ is = (1)
Hence, the answer is (1).
Question 10: The number of paramagnetic species from the following is
$\begin{aligned}
& {\left[\mathrm{Ni}(\mathrm{CN})_4\right]^{2-},\left[\mathrm{Ni}(\mathrm{CO})_4\right],\left[\mathrm{NiCl}_4\right]^{2-}} \\
& {\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{4--},\left[\mathrm{Cu}\left(\mathrm{NH}_3\right)_4\right]^{2+}} \\
& {\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{3-} \text { and }\left[\mathrm{Fe}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right]^{2+}}
\end{aligned}$
Solution:
$
\left(\mathrm{NiCl}_4\right)^{-2} \rightarrow \mathrm{Ni}^{+2} \rightarrow 3 \mathrm{~d}^8
$
$\mathrm{Cl}^{+} \rightarrow$ Weak field layered
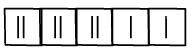
$\left(\mathrm{Cu}\left(\mathrm{NH}_3\right)_4\right)^{2+} \rightarrow \mathrm{Cu}^{+2} \rightarrow 3 \mathrm{~d}^9$
Unpaired $\mathrm{e}^{-}=1$, paramagnetic
$
\left(\mathrm{Fe}(\mathrm{CN})_6\right)^{-3} \rightarrow \mathrm{Fe}^{+3} \rightarrow 3 \mathrm{~d}^5
$
CN-is strong field ligand
so Unpaired e- = 1
so paramagnetic
$
\left.\left(\mathrm{Fe}_{\left(\mathrm{H}_2 \mathrm{O}\right.}\right)_6\right)^{+2} \rightarrow \mathrm{Fe}^{+2} \rightarrow 3 \mathrm{~d}^6
$
$\mathrm{H}_2 \mathrm{O}$ is weak field ligand
Hence, the answer is (4).
Question 11: Given below are two statements: one is labeled as Assertion (A) and the other is labeled as Reason(R).
Assertion (A): Ketoses give Seliwanoff's test faster than Aldoses.
Reason (R): Ketoses undergo -elimination followed by the formation of furfural.
In the light of the above statements, choose the correct answer from the options given below :
1) (A) is false but (R) is true
2) (correct) (A) is true but (R) is false
3) Both (A) and (R) are true but (R) is not the correct explanation of (A)
4) Both (A) and (R) are true and (R) is the correct explanation of (A)
Solution:
Seliwanoff’s test – Test to differentiate between ketose and aldose.
In this keto hexose is more rapidly dehydrated to form $5-$hydroxy methyl furfural when heated in an acidic medium which on condensation with resorcinol, results brown colored complex.
Hence, the answer is the option (2).
Question 12: A projectile is projected at $30^{\circ}$ from horizontal with initial velocity $40 \mathrm{~ms}^{-1}$. The velocity of the projectile at $\mathrm{t}=2 \mathrm{~s}$ from the start will be :
(Given $g=10 \mathrm{~m} / \mathrm{s}^2$ )
1) Zero
2) (correct) $20 \sqrt{3} \mathrm{~ms}^{-1}$
3) $40 \sqrt{3} \mathrm{~ms}^{-1}$
4) $20 \mathrm{~ms}^{-1}$
Solution:

$\begin{aligned} & \mathrm{U}_{\mathrm{x}}=40 \cos 30=20 \sqrt{3} \\ & \mathrm{U}_{\mathrm{y}}=40 \sin 30=20 \\ & \mathrm{~V}_{\mathrm{x}}=20 \sqrt{3} \\ & \mathrm{~V}_{\mathrm{y}}=\mathrm{u}_{\mathrm{y}}-\mathrm{gt}=20-10 \times 2=0 \\ & \mathrm{~V}=\sqrt{\mathrm{v}_{\mathrm{x}}^2+\mathrm{v}_{\mathrm{y}}^2}=20 \sqrt{3}=\mathrm{ms}^{-1}\end{aligned}$
Hence, the answer is option (2).
Question 13: Consider the following sequence of reactions :
Molar mass of the product formed (A) is _________$\mathrm{g} \mathrm{mol}^{-1}$
Solution:
.
Biphenyl (C12 H10)
Molar mass= 120 x 12 x +10 x1 = 154$\mathrm{g} \mathrm{mol}^{-1}$.
Hence, the answer is 154.
Question 14:
The ratio of the de-Broglie wavelengths of proton and electron having the same Kinetic energy: (Assume $\mathrm{m}_{\mathrm{p}}=\mathrm{m}_{\mathrm{e}} \times 1849$ )
1) 1:62
2) 1:30
3) (correct) 1: 43
4) 2: 43
Solution:
$\begin{aligned}
& \lambda=\frac{\mathrm{h}}{\mathrm{P}}=\frac{\mathrm{h}}{\sqrt{2 \mathrm{mK}}} \\
& \frac{\lambda_{\mathrm{P}}}{\lambda_{\mathrm{e}}}=\sqrt{\frac{\mathrm{m}_{\mathrm{e}}}{\mathrm{~m}_{\mathrm{p}}}}=\sqrt{\frac{\mathrm{m}_{\mathrm{e}}}{1840 \mathrm{me}}}=\frac{1}{\sqrt{1840}} \\
& \frac{\lambda_{\mathrm{P}}}{\lambda_{\mathrm{e}}}=\frac{1}{43}
\end{aligned}$
Hence, the answer is the option (3).
Question 15: 5 g of NaOH was dissolved in deionized water to prepare a 450 mL stock solution this solution would be required to prepare 500 mL of 0.1 M solution?
Given: Molar Mass of $\mathrm{Na}, \mathrm{O}$ and H is 23,16 and $1 \mathrm{~g} \mathrm{~mol}^{-1}$ respectively
Solution:
Molarity of stock solution
$\begin{aligned}
& =\frac{5 / 40}{450} \times 1000 \\
& =\frac{50}{4 \times 45}=\frac{10}{36} \mathrm{M} \\
& \mathrm{M}_1 \mathrm{~V}_1=\mathrm{M}_2 \mathrm{~V}_2 \\
& \frac{10}{36} \times \mathrm{V}=0.1 \times 500 \\
& \mathrm{~V}=\frac{50 \times 36}{10}=180 \mathrm{ml}
\end{aligned}$
Hence, the answer is (180).
Question 16: Three identical resistors with resistance $\mathrm{R}=12 \Omega$ and two identical inductors with self inductance $\mathrm{L}=5 \mathrm{mH}$ are connected to an ideal battery with emf of $
12 \mathrm{~V}
$ as shown in the figure. The current through the battery long after the switch has been closed will be _______ A.
Solution:
After a long time, an inductor behaves as a resistance-less path.
i.e Short all inductor
$\begin{aligned} & \text { Req. }=\frac{\mathrm{R}}{3}=\frac{12}{3}=4 \Omega \\ & \mathrm{I}=\frac{12}{4}=3 \mathrm{~A}\end{aligned}$
Hence, the answer is option (1).
Question 17: An electron with mass ' $m$ ' with an initial velocity $(t=0) \vec{v}=v_0 \hat{i} \quad\left(v_0>0\right)$ enters a magnetic field $\overrightarrow{\mathrm{B}}=\mathrm{B}_0 \hat{\mathrm{j}}$. If the initial deBroglie wavelength at $\mathbf{t}=\mathbf{0}$ is $\lambda_0$ then its value after time ' t ' would be :
1) $\frac{\lambda_0}{\sqrt{1-\frac{\mathrm{e}^2 \mathrm{~B}_0^2 \mathrm{t}^2}{\mathrm{~m}^2}}}$
2) $\frac{\lambda_0}{\sqrt{1+\frac{e^2 B_0^2 t^2}{m^2}}}$
3) $\lambda_0 \sqrt{1+\frac{\mathrm{e}^2 \mathrm{~B}_0^2 \mathrm{t}^2}{\mathrm{~m}^2}}$
4) (correct) $\lambda_0$
Solution:
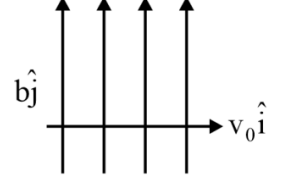
$
\lambda=\frac{\mathrm{R}}{\mathrm{P}}=\frac{\mathrm{h}}{\mathrm{mv}_0}
$
speed will not change in magnetic field $\left(\lambda_0\right)$
Hence, the answer is option (4)
Question 18: In the digital circuit shown in the figure, for the given inputs the P and Q values are :
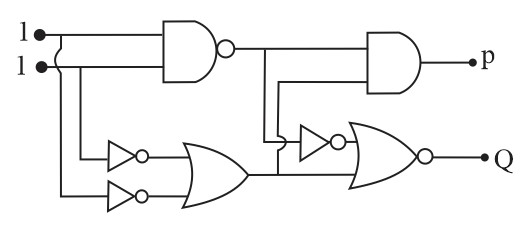
1) $P=1, Q=1$
2) $P=0, Q=0$
3) $P=0, Q=1$
4) $P=1, Q=0$
Solution:
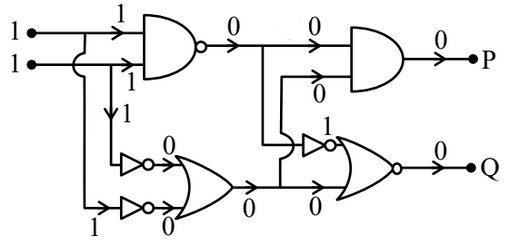
Hence, the answer is option (2)
Question 19: Let $\alpha$ be the area of the larger region bounded by the curve y $2=8 x$ and the lines $y=x$ and $x=2$, which lies in the first quadrant. Then the value of $3 \alpha$ is equal to
Solution:
$\operatorname{area}(\alpha)=\int_2^8(2 \sqrt{2} \sqrt{x}-x) d x$
$\begin{aligned} & =\left[2 \sqrt{2} \cdot \frac{2}{3} \mathrm{x}^{3 / 2}-\frac{x^2}{2}\right]^8 \\ & =\frac{4 \sqrt{2}}{3}[8 \times 2 \sqrt{2}-2 \sqrt{2}]-30 \\ & =\frac{28 \times 4}{3}-30 \\ & =\frac{112}{3}-30 \\ & \alpha=\frac{22}{3} \\ & 3 \alpha=22\end{aligned}$
Hence, the answer is 22.
Question 20: Let $y=y(x)$ be the solution curve of the differential equation
$x\left(x^2+e^x\right) d y+\left(e^x(x-2) y-x^3\right) d x=0, x>0$
passing through the point $(1,0)$. Then $y(2)$ is equal to :
1) $\frac{4}{4-\mathrm{e}^2}$
2) $\frac{2}{2+\mathrm{e}^2}$
3) $\frac{2}{2-\mathrm{e}^2}$
4) (correct) $\frac{4}{4+\mathrm{e}^2}$
Solution :
For this given differential equation:
$x\left(x^2+e^x\right) d y+\left(e^x(x-2) y-x^3\right) d x=0$
$x\left(x^2+e^x\right) \frac{d y}{d x}+e^x(x-2) y=x^3$
$\frac{d y}{d x}+\frac{e^x(x-2)}{x\left(x^2+e^x\right)} y=\frac{x^2}{x^2+e^x}$
$P(x) = \frac{e^x(x - 2)}{x(x^2 + e^x)}=\frac{2 x+e^x}{x^2+e^x}-\frac{2}{x}$
$Q(x) = \frac{x^2}{x^2 + e^x}$
The integrating factor:
$\begin{aligned} & \text { IF }=e^{\int p d x}=e^{\int\left(\frac{2 x+e^x}{x^2+e^x}-\frac{2}{x}\right) d x} \\ & =e^{\ln \left(x^2+e^x\right)-2 \ln x} \\ & =e^{\ln \left(\frac{x^2+e^x}{x^2}\right)} \\ & =\frac{x^2+e^x}{x^2}=1+\frac{e^x}{x^2} \\ & y\left(1+\frac{e^x}{x^2}\right)=\int \frac{x^2}{x^2+e^x} \frac{x^2+e^x}{x^2} \\ & y\left(1+\frac{e^x}{x^2}\right)=x+\lambda \\ & y(1)=0 \Rightarrow \lambda=-1 \\ & y=\frac{(x-1) x^2}{x^2+e^x}\end{aligned}$
$y(2)=\frac{4}{4+e^2}$
Hence, the answer is option (4).
Question 21: Two wires $A$ and $B$ are made of the same material, having ratio of lengths $\frac{L_A}{L_B}=\frac{1}{3}$ and their diameter ratio $\frac{d_A}{d_B}=2$. If both the wires are stretched using the same force, what would be the ratio of their respective elongations?
1) 1 : 6
2) (correct) 1 : 12
3) 3 : 4
4) $1: 3$
Solution:
$\begin{aligned}
& \frac{\mathrm{L}_{\mathrm{A}}}{\mathrm{~L}_{\mathrm{B}}}=\frac{1}{3} \text { and } \frac{\mathrm{d}_{\mathrm{A}}}{\mathrm{~d}_{\mathrm{B}}}=2 \\
& \Delta \mathrm{~L}_{\mathrm{A}}=\frac{\mathrm{F}_{\mathrm{A}} \mathrm{~L}_{\mathrm{A}}}{\mathrm{~A}_{\mathrm{A}} \mathrm{Y}_{\mathrm{A}}} \text { and } \Delta \mathrm{L}_{\mathrm{B}}=\frac{\mathrm{F}_{\mathrm{B}} \mathrm{~L}_{\mathrm{B}}}{\mathrm{~A}_{\mathrm{B}} \mathrm{Y}_{\mathrm{B}}}
\end{aligned}$
Given, $\mathrm{F}_{\mathrm{A}}=\mathrm{F}_{\mathrm{B}}$ and $\mathrm{Y}_{\mathrm{A}}=\mathrm{Y}_{\mathrm{B}}$
$\begin{aligned}
& \frac{\Delta L_A}{\Delta L_B}=\frac{\frac{\mathrm{F}_{\mathrm{A}} \mathrm{~L}_{\mathrm{A}}}{\mathrm{~A}_{\mathrm{A}} \mathrm{Y}_{\mathrm{A}}}}{\frac{\mathrm{~F}_{\mathrm{B}} \mathrm{~L}_{\mathrm{B}}}{\mathrm{~A}_{\mathrm{B}} \mathrm{Y}_{\mathrm{B}}}}=\left(\frac{\mathrm{L}_{\mathrm{A}}}{\mathrm{~L}_{\mathrm{B}}}\right)\left(\frac{\mathrm{A}_{\mathrm{B}}}{\mathrm{~A}_{\mathrm{A}}}\right) \\
& \frac{\Delta \mathrm{L}_{\mathrm{A}}}{\Delta \mathrm{~L}_{\mathrm{B}}}=\left(\frac{\mathrm{L}_{\mathrm{A}}}{\mathrm{~L}_{\mathrm{B}}}\right)\left(\frac{\frac{\pi}{4} \mathrm{~d}_{\mathrm{B}}^2}{\frac{\pi}{4} \mathrm{~d}_{\mathrm{A}}^2}\right)=\left(\frac{\mathrm{L}_{\mathrm{A}}}{\mathrm{~L}_{\mathrm{B}}}\right)\left(\frac{\mathrm{d}_{\mathrm{B}}}{\mathrm{~d}_{\mathrm{A}}}\right)^2 \\
& \frac{\Delta \mathrm{~L}_{\mathrm{A}}}{\Delta \mathrm{~L}_{\mathrm{B}}}=\left(\frac{1}{3}\right)\left(\frac{1}{2}\right)^2=\frac{1}{12}
\end{aligned}$
Hence, the answer is option (2).
Question 22: A sample of a liquid is kept at 1 atm . It is compressed to 5 atm which leads to change of volume of $0.8 \mathrm{~cm}^3$. If the bulk modulus of the liquid is 2 GPa , the initial volume of the liquid was $\_\_\_\_$ litre. (Take $1 \mathrm{~atm}=10^5 \mathrm{~Pa}$ )
Solution:
Given,
Initial pressure of liquid $\left(\mathrm{P}_{\mathrm{i}}\right)=1 \mathrm{~atm}$
Final pressure of liquid $\left(\mathrm{P}_{\mathrm{f}}\right)=5 \mathrm{~atm}$
Change in pressure $(d P)=P_f-P_i=4 \mathrm{~atm}$
$=4 \times 10^5 \mathrm{~Pa}$
Change in volume $(\mathrm{dV})=-0.8 \mathrm{~cm}^3$
Bulk modulus $(\mathrm{B})=2 \times 10^9 \mathrm{~Pa}$
Now,
$\begin{aligned}
& B=\frac{-d P}{(d V / V)} \Rightarrow V=-B\left(\frac{d V}{d P}\right) \\
& \Rightarrow \mathrm{V}=-2 \times 10^9 \times \frac{\left(-0.8 \times 10^{-6}\right)}{4 \times 10^5}=4 \times 10^{-3} \mathrm{~m}^3=4 \text { litre }
\end{aligned}$
Hence, the answer is 4.
Question 23: From the magnetic behaviour of $\left[\mathrm{NiCl}_4\right]^{2-}$ (paramagnetic) and $\left[\mathrm{Ni}(\mathrm{CO})_4\right]$ (diamagnetic), choose the correct geometry and oxidation state.
1) $\left[\mathrm{NiCl}_4\right]^{2-}: \mathrm{Ni}^{\mathrm{II}}$, square planar
$\left[\mathrm{Ni}(\mathrm{CO})_4\right]: \mathrm{Ni}(0)$, square planar
2) (correct) $\left[\mathrm{NiCl}_4\right]^{2-}: \mathrm{Ni}^{\mathrm{II}}$, tetrahedral $\left[\mathrm{Ni}(\mathrm{CO})_4\right]: \mathrm{Ni}(0)$, tetrahedral
3) $\left[\mathrm{NiCl}_4\right]^{2-}: \mathrm{Ni}^{\mathrm{II}}$, tetrahedral $\left[\mathrm{Ni}(\mathrm{CO})_4\right]: \mathrm{Ni}^{\mathrm{II}}$, square planar
4) $\left[\mathrm{NiCl}_4\right]^{2-}: \mathrm{Ni}(0)$, tetrahedral
$\left[\mathrm{Ni}(\mathrm{CO})_4\right]: \mathrm{Ni}(0)$, square planar
Solution:
$\left[\mathrm{NiCl}_4\right]^{2-}$
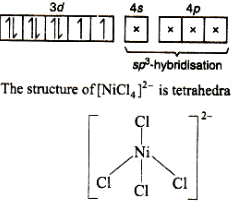
$\mathrm{Ni}^{+2}-[\mathrm{Ar}] 3 \mathrm{~d}^8 4 \mathrm{~s}^0 \rightarrow \mathrm{sp}^3$, Tetrahedral
Number of unpaired electron $=2$ paramagentic
$\left[\mathrm{Ni}(\mathrm{CO})_4\right]$,
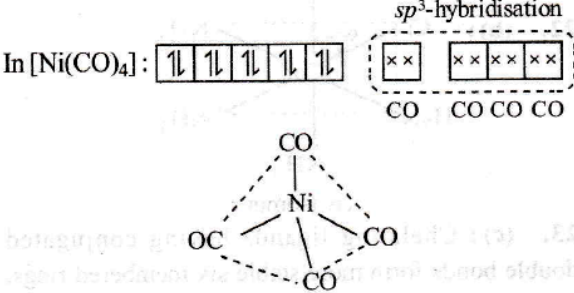
$\mathrm{Ni}(0) \rightarrow[\mathrm{Ar}] 3 \mathrm{~d}^{10} 4 \mathrm{~s}^0$ (After rearrangement)
No unpaired electron
$\mathrm{sp}^3$, Tetrahedral, Diamagnetic
Hence, the correct answer is option (2).
Question 24: Let $f(x)$ be a positive function and $I_1=\int_{-\frac{1}{2}}^1 2 x f(2 x(1-2 x)) d x$ and $I_2=\int_{-1}^2 f(x(1-x)) d x$. Then the value of $\frac{I_2}{I_1}$ is equal to $\_\_\_\_$
1) 9
2) 6
3) 12
4) (correct) 4
Solution:
$\begin{aligned} & I_1=\int_{-\frac{1}{2}}^1 2 x f(2 x(1-2 x) d x) \\ & I_1=\int_{-\frac{1}{2}}^1 2\left(\frac{1}{2}-x\right) f\left(2\left(\frac{1}{2}-x\right)\left(1-2\left(\frac{1}{2}-x\right)\right)\right) d x \\ & I_1=\int_{-\frac{1}{2}}^1(1-2 x) f((1-2 x)(2 x)) d x\end{aligned}$
$\begin{aligned} & I_1=\int_{-\frac{1}{2}}^1 f((1-2 x)(2 x)) d x-\int_{-\frac{1}{2}}^1 2 x \underbrace{f((1-2 x)(2 x)) d x}_{I_1} \\ & 2 I_1=\int_{-\frac{1}{2}}^1 f((1-2 x)(2 x)) d x\end{aligned}$
Put $2 x=t$
$\begin{aligned}
& 2 d x=d t \\
& d x=\frac{d t}{2} \\
& 2 I_1=\frac{1}{2} \int_{-1}^2 f((1-t)(t)) d t \\
& I_1=\frac{1}{4} \int_{-1}^2 f((1-x)(x)) d x \\
& I_1=\frac{1}{4} I_2 \\
& 4 \Rightarrow \frac{I_2}{I_1}
\end{aligned}$
Hence, the answer is option (4).
Question 25: Let the domain of the function $f(x)=\log _2 \log _4 \log _6\left(3+4 x-x^2\right)$ be $(a, b)$. If $\int_0^{\mathrm{b}-\mathrm{a}}\left[\mathrm{x}^2\right] \mathrm{dx}=\mathrm{p}-\sqrt{\mathrm{q}}-\sqrt{\mathrm{r}}, \mathrm{p}, \mathrm{q}, \mathrm{r} \in \mathrm{N}, \operatorname{gcd}(\mathrm{p}, \mathrm{q}, \mathrm{r})=1$, where $[\cdot]$ is the greatest integer function, then $\mathrm{p}+\mathrm{q}+\mathrm{r}$ is equal to
1) (correct) 10
2) 8
3) 11
4) 9
Solution:
We need:
$\log_4 \log_6(3 + 4x - x^2) > 0$
This implies:
$\log_6(3 + 4x - x^2) > 1$
$3 + 4x - x^2 > 6$
$x^2 - 4x + 3 < 0$
$(x - 1)(x - 3) < 0 \Rightarrow x \in (1, 3)$
So domain is $(a, b) = (1, 3) \Rightarrow b - a = 2$
Now compute:
$\int_0^2 [x^2] \, dx$
Break into intervals based on $x^2$:
$[x^2] = 0$ for $x \in [0,1)$
$[x^2] = 1$ for $x \in [1,\sqrt{2})$
$[x^2] = 2$ for $x \in [\sqrt{2},\sqrt{3})$
$[x^2] = 3$ for $x \in [\sqrt{3},\sqrt{4})$
Recognized as Institute of Eminence by Govt. of India | NAAC ‘A++’ Grade | Upto 75% Scholarships
98% Placement Record | Highest CTC 81.25 LPA | NAAC A++ Accredited | Ranked #62 in India by NIRF Ranking 2025 | JEE & JET Scores Accepted
So the integral becomes:
$\int_0^1 0\,dx + \int_1^{\sqrt{2}} 1\,dx + \int_{\sqrt{2}}^{\sqrt{3}} 2\,dx + \int_{\sqrt{3}}^{2} 3\,dx$
$=(\sqrt{2} - 1) + 2(\sqrt{3} - \sqrt{2}) + 3(2 - \sqrt{3})$
$= 5 - \sqrt{2} - \sqrt{3}$
Thus,
$p = 5,\ q = 2,\ r = 3 \Rightarrow p + q + r = 10$
Hence, the answer is option (1).
Frequently Asked Questions (FAQs)
The top 25 repeated questions typically cover:
Physics: Kinematics, Newton’s Laws of Motion, Work-Energy-Power, Rotational Motion, Thermodynamics, and Semiconductor Devices.
Chemistry: Periodic Table Trends, Chemical Bonding, Coordination Compounds, Organic Chemistry (e.g., Reactions, Isomerism), and Stoichiometry.
Mathematics: Calculus (Differentiation), Coordinate Geometry, Algebra, and Matrices and Determinants.
These questions are highly repeated, and high-weightage problems in previous JEE Mains papers. Solving them ensures the
Speed and Accuracy: Regular practice reduces question-solving time.
Confidence: Experience with the same patterns suggests that accuracy will improve.
Time Allocation: You can quickly solve these questions and focus the remaining time on others.
Recommended books for JEE mains are given below:
Physics: "Concepts of Physics" by H.C. Verma (for theory + problems), JEE Mains-specific problem books.
Chemistry: NCERT Textbooks for Inorganic/Physical Chemistry, "Organic Chemistry" by Morrison and Boyd.
Mathematics: "IIT Mathematics" by M.L. Khanna, Arihant Series for targeted topics.
The common mistakes are:
Over-dependence on shortcuts: Understand the use of these formulas, not just the reproduction of them.
Ignoring weak points: Don't shy away from those difficult topics-look at your mistakes and the concepts again.
On Question asked by student community
Usha Mittal of Technology has no AI quota officially. please contact the college for any mangement quota seats.
decent chances actually as home state quota seats are 50%. allotments will depend on the JEE rank and not percentile though. in 2025, for female supernumerary it closed at 9286 rank while for open gen it closed at 5573.
So, would advise to use this tool to check the probable
yes you will. Ususally the return is within 7 days i it has failed at the gateway level which it seems to be. Please wait. You will get the money back
Slim chances as in 2025 the closing rank was 118 for SPA Delhi for B.Arch. You will need to wait for the rank list to come in April before getting a better picture. Please check https://engineering.careers360.com/jee-main-college-predictor for the predictions.
Check out https://engineering.careers360.com/jee-main-rank-predictor to know the probable rank
Hi Smita Sharma,
With 47 percentile in JEE Mains 2026, you might get rank around 7,00,000 plus which is very high. Check the link below for the Best engineering colleges available for you based on yours percentile.
Link 1: https://engineering.careers360.com/colleges/list-of-engineering-colleges-in-pune-accepting-jee-main
Among top 100 Universities Globally in the Times Higher Education (THE) Interdisciplinary Science Rankings 2026
Recognized as Institute of Eminence by Govt. of India | NAAC ‘A++’ Grade | Upto 75% Scholarships
70th University Ranked by NIRF | 80th Engineering Rank by NIRF | Accredited by NBA and NAAC A+
Last Date to Apply: 26th March | Ranked #43 among Engineering colleges in India by NIRF | Highest Package 1.3 CR , 100% Placements
Highest CTC 44.14 LPA | UGC Approved | 1600+ Recruiters | 100% Placement
NAAC A++ Grade | Recognized as Category-1 Deemed to be University by UGC | 41,000 + Alumni Imprints Globally