JEE Main: Newton's Law Of Cooling

Newton's Law Of Cooling - Isaac Newton developed Newton's Law of Cooling in 1701. He noticed that the rate of heat loss (change in temperature) of a body is directly proportional to the temperature difference between the body and its surroundings. Newton was the first scientist who analysed the relationship between the rate of heat loss from a body in a certain enclosure and its surface area exposed. He was primarily focused on heat transfer by radiation.

Also Check: Crack JEE Main 2025 - Join Our Free Crash Course Now!

JEE Main 2025: Sample Papers | Syllabus | Mock Tests | PYQs | Video Lectures

JEE Main 2025: Preparation Guide | High Scoring Topics | Study Plan 100 Days

This law defines the rate at which a body changes its temperature by radiation, which is almost equal to the temperature difference between the body itself and its surroundings. Keep in mind that the temperature difference over here is very small. Initially the law was not agreed upon in its present form. The present form of the Law Of Cooling was created, after the confusion between the concepts of heat and temperature, much after 1701.

Definition of Newton’s Law of Cooling

In simpler terms, Newton’s Law of Cooling states that the rate of loss of heat from a body is directly proportional to the temperature difference of the body and its surroundings.

Newton’s Law of Cooling is represented by:

– dQ/dt ∝ (T_t – T_s)

– dQ/dt = k (T_t – T_s) …………………(1)

Where,

T_t = Body (Object) temperature at time t

T_s = temperature of the surrounding,

k = Constant (Positive) that depends on the nature of the surface of the object and the area of the object and under consideration.

Formula of Newton’s Law of Cooling

The Newton's laws of cooling can be represented by the following formula-

T(t) = T_s + (T_t - T_s ) e^-kt

Where,

T(t) = Temperature at time t

T_s = Temp of surroundings (Ambient temperature)

T_t = Initial temperature of the hot object (body)

k = positive constant and

t = time

Newton's Laws of Cooling Derivation:

Let a body of mass m, specific heat capacity s, at temperature T_t and surrounding temperature T_s. If the change in temperature is dT_t in time dt, then the amount of heat lost is given by,

dQ = m*s dT_t

The rate of heat loss is given by,

dQ/dt = ms (dT_t/dt) ……………………………… (2)

Compare the equations (1) and (2) as,

– ms (dT_t/dt) = k (T_t – T_s)

After Rearrange the above equation

dT_t/(T_t–T_s) = – (k /ms) dt

dT_t /(T_t – T_s) = – Kdt

After integrating the above expression,

log_e (T_t – T_s) = – K t + c

or

T_t = T_s + C’ e^–Kt

where C’ = e^c

In general, T(t) = T_s + (T_t - T_s ) e^-kt

Limitations of Newton's Law of Cooling

• The temperature difference between the environment and the body must be very small.

• For the loss of heat from the body only radiation should be used.

• During the cooling of the object or body the temperature of the surroundings must remain constant (This is the key constraint of Newton’s law of cooling).

Applications of Newton’s Law of Cooling

• It helps to identify the time of death by determining the temperature difference at the time of death and the current body temperature.

• To estimate how much time it will take a warm object to cool down at a specific temperature.

• To determine the temperature of an object or drink in a refrigerator after some time has been passed.

• It is also helpful to determine the temperature of the water heater. And how it cools down.

• For low temperature, Newton's laws of cooling is used in determining the ambient conditions for nuclear reaction.

Previous Years JEE Main Questions

Q-1 (JEE Main 2022)

In an experiment to verify Newton's law of cooling, a graph is plotted between the temperature difference of the water and surroundings and time as shown in figure. The initial temperature of water is taken as . The value of , as mentioned in the graph will be______.

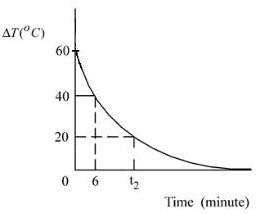
Solution:

Rate of cooling:

$$
R=\frac{-\Delta T}{\Delta t}
$$

At $\mathrm{t}=0=\mathrm{k}\left(\mathrm{T}_{\mathrm{avg}}-\mathrm{T}_0\right)$
$\mathrm{T}_1=80^{\circ} \mathrm{C}=$ Temperature of water
$T_1-T_{\text {surrounding }}=60$
$T_0=T_{\text {surrounding }}=20^{\circ} \mathrm{C}$
At $t=6 \mathrm{~s}$
$T_{\text {temperature of water }}^t=T_2$
$T_2-T_{\text {surrounding }}=40$
$T_2=60$
At time $=t_2$
Temperature of water $=T_3$
$T_3-T_{\text {sur rounding }}=20$
$T_3=40^{\circ} \mathrm{C}$
from $t=0$ to $t=6 \mathrm{~s}$
$-\frac{\Delta T}{\Delta t}=-\frac{\left(T_2-T_1\right)}{\Delta t}=K\left(\frac{T_1+T_2}{2}-T_0\right)$
$\frac{20}{6}=K(70-20)$
$k=\frac{1}{15} \rightarrow(1)$

$$
\begin{aligned}
& \text { From } t=0 \text { to } t=t_2 \\
& \begin{aligned}
-\frac{\Delta t}{\Delta t} & =\frac{-\left(t_3-t_2\right)}{2+\left(t_2-0\right)}=k\left(\frac{t_2+T_3}{2}-T_0\right) \\
\frac{20}{t_2} & =\left(\frac{1}{15}\right) \\
t_2 & =10 \mathrm{~min}
\end{aligned}
\end{aligned}
$$

Q-2 (JEE Main 2021)

A body takes 4 min to cool from 61 degree Celsius to 59 degree Celsius. If the temperature of the surroundings is 30 degree Celsius the time taken by the body to cool from 51 degree Celsius to 49 degree Celsius is:

Solution:

By Newton's law of cooling ,

$\begin{aligned} & \frac{-\Delta T}{\Delta t}=K\left(T_{a v g}-T_0\right) \\ & \left(\frac{61-59}{4}\right)=\left(\frac{2}{4}\right)=k\left(\frac{61+59}{2}-30\right) \rightarrow(1) \\ & \frac{(51-49)}{t}=\frac{2}{t}=k\left(\frac{51+49}{2}-30\right) \rightarrow(2) \\ & \frac{2 / 4}{2 / t}=\frac{k(60-30)}{k(50-30)} \\ & \frac{t}{4}=\frac{30}{20} \\ & t=6 \mathrm{~min}\end{aligned}$

Hence it will take 6 min to cool down from 51 degree Celsius to 49 degree Celsius.

Q-3 (JEE Main 2020)

\text { A metallic sphere cools from } 50^{\circ} \mathrm{C} \text { to } 40^{\circ} \mathrm{C} \text { in } 300 \mathrm{~s} \text {. If atmospheric temperature around is } 20^{\circ} \mathrm{C} \text {. then the sphere's temperature after the next } 5 \text { minutes will be close to: }

Solution:

$$
\text { As } \frac{\Delta T}{\Delta t}=k\left[\frac{T_f+T_i}{2}-T_0\right]
$$

From question

$$
\begin{aligned}
& \frac{50-40}{3(00}=k\left[\frac{90}{2}-20\right] \ldots(1 \\
& \frac{40-T}{3000}=k\left[\frac{40+T}{2}-20\right] \ldots
\end{aligned}
$$

Taking ratio of equation (1) and(2) we get

$$
\begin{aligned}
& \frac{10}{40-T}=\left[\frac{50}{40+T-40}\right] \\
& \mathrm{T}=200-5 \mathrm{~T} \\
& 6 \mathrm{~T}=200 \\
& \Rightarrow \mathrm{~T}=33^0 \mathrm{C}
\end{aligned}
$$

NCERT Practice Questions For Newton's Law of Cooling

This topic is from NCERT class 11 chapter Heat and Thermodynamics. Following are some practice questions based on the concept Newton's laws of cooling from NCERT class 11.

Q-1: A pan filled with hot food cools from 94 °C to 86 °C in 2 minutes when the room temperature is at 20 °C. How long will it take to cool from 71 °C to 69 °C?

Solution:

Given That food cools from 94 °C to 86 °C in 2 minutes.

We can calculate an average temperature of 94 °C and 86 ° C. That is 90 °C. The food cools down 8°C in two minutes. Change in temperature from room temperature 20 °C is 70 °C

Change in temperature/Time = K ∆T

8/2 = K(70).........(1)

We want to calculate the time taken for food to cool down 71 °C to 69 °C.

Average temperature of 71 °C to 69 °C is 70°C

The temperature difference between room temperature 20°C and 70 is 50°C

∆T = 50°C

Using the formula

Change in temperature/Time = K ∆T

Change in temperature from 71 °C to 69 °C is equal to 2 °C and let's consider the time taken to cool down.

2/t = K (50) …………(2)

Using equation (1) and (2)

(8/2)/(2/t) = 70/50

t= 7/10 = 0.7 min or 42 second

Hence food cools down form 71 °C to 69 °C in 42 seconds

Q-2: A body cools from 80 °C to 50 °C in 5 minutes. Calculate the time it takes to cool from 60 °C to 30 °C. The temperature of the surroundings is 20 °C.

Solution:

Given That a body cools down 80 °C to 50 °C in 5 minutes and surrounding temperature = 20 °C

We want to find out the time taken by the body to cool down from 60 °C to 30 °C.

We know that here we can apply newton's law of cooling and we can use formula

Change in temperature/Time = K ∆T

For first case change in average temperature for 80 °C and 50 °C = 65 °C

The difference between 65°C and surrounding temperature 20°C is 45°C.

It cools down 30°C in 5 min

Therefore

30/5 = K (45) ……….(1)

For second case

Average temperature of 60 °C to 30 °C is 45°C.

The temperature difference between 45°C and surrounding temperature 20°C is 25°C.

Body cools down 30°C in lets take T minutes.

Using the formula

Change in temperature/Time = K ∆T

30/T = K (25) ………..(2)

Using equation (1) and (2)

T/5 = 45/25

T = 9 min

Hence, body will take 9 min to cools down from 60 °C to 30 °C

Newton's Law of Cooling provides important insights as it is used in fields like forensic science hence, it becomes important from exam point of view as well. To solve most of the questions from these topics, understanding of the basic concepts is required.