Amity University-Noida B.Tech Admissions 2026
Among top 100 Universities Globally in the Times Higher Education (THE) Interdisciplinary Science Rankings 2026
If you want to crack JEE Mains, you need to understand the concepts along with increasing speed and accuracy to solve the application problems and become familiar with the exam pattern overall. The JEE Mains 2026 Exam Booster Series has been developed to help aspirants reach their dream percentile as a 30-day targeted preparation plan. Each day, you'll get the following:
This Story also Contains

3 Daily Questions: One Question from Physics, Chemistry, and Mathematics, concentrating on Higher Frequency PYQs and the Most Repeated JEE Topics.
Daily PDF: 10 Additional Questions for Practice, which would strengthen the understanding of the concepts and enhance problem-solving speed.
Concept Focus: Questions selected from high-yield, historically valuable topics to secure marks among the top ranks.
Sticking with the series for a period of 30 days will lead you to practice more than 90 high-impact questions, along with 300 extra PDF PYQs-in all major chapters in a systematic manner.
Full Length Test: Physics test paper prepared as per the JEE Main pattern.
It is designed to help students assess their overall understanding and exam readiness in Physics.
|
Daily PDF |
Full Length Test: Chemistry test paper prepared as per the JEE Main pattern.
It is designed to help students assess their overall understanding and exam readiness in Chemistry.
|
Daily PDF |
Full Length Test: Mathematics test paper prepared as per the JEE Main pattern.
It is designed to help students assess their overall understanding and exam readiness in Mathematics.
|
Full Length Test |
Full Length Test: Physics test paper prepared as per the JEE Main pattern.
It is designed to help students assess their overall understanding and exam readiness in Physics.
|
Daily PDF |
Full Length Test: Chemistry test paper prepared as per the JEE Main pattern.
It is designed to help students assess their overall understanding and exam readiness in Chemistry.
|
Daily PDF |
Full Length Test: Mathematics test paper prepared as per the JEE Main pattern.
It is designed to help students assess their overall understanding and exam readiness in Mathematics.
|
Full Length Test |
Laws of Motion: Equilibrium of concurrent forces is a frequently asked concept of this chapter
Question:
A body of mass $m$ is suspended by two strings making angles $\theta_1$ and $\theta_2$ with the horizontal ceiling with tensions $\mathrm{T}_1$ and $\mathrm{T}_2$ simultaneously. $\mathrm{T}_1$ and $\mathrm{T}_2$ are related by $T_1=\sqrt{3} T_2$. the angles $\theta_1$ and $\theta_2$ are

1) $\theta_1=30^{\circ}, \theta_2=60^{\circ} \text { with } \mathrm{T}_2=\frac{3 \mathrm{mg}}{4}$
2) (correct) $\theta_1=60^{\circ}, \theta_2=30^{\circ} \text { with } \mathrm{T}_2=\frac{\mathrm{mg}}{2}$
3) $\theta_1=45^{\circ}, \theta_2=45^{\circ} \text { with } \mathrm{T}_2=\frac{3 \mathrm{mg}}{4}$
4)$\theta_1=30^{\circ}, \theta_2=60^{\circ} \text { with } \mathrm{T}_2=\frac{4 \mathrm{mg}}{5}$
Solution:
$\mathrm{T}_1 \sin \theta_1+\mathrm{T}_2 \sin \theta_2=\mathrm{mg}$
$\mathrm{~T}_1=\sqrt{3} \mathrm{~T}_2 $
$ \Rightarrow \mathrm{~T}_2\left[\sqrt{3} \sin \theta_1+\sin \theta_2\right]=\mathrm{mg} $
$ \text { for } \theta_1=60^{\circ} \& \theta_2=30^{\circ} $
$ \mathrm{T}_2=\frac{\mathrm{mg}}{2}$
Hence, the answer is the option (2).
|
Daily PDF |
Organic Compounds Containing Nitrogen: Azo-Coupling Reaction is the scoring topic of this chapter.
Question: The sequence from the following that would result in giving predominantly $3,4,5$ - Tribromoaniline is :
1)

2)
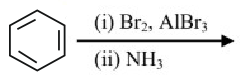
3)
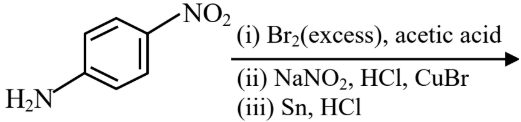
4)
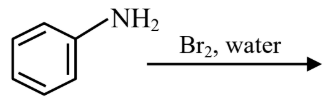
Solution:

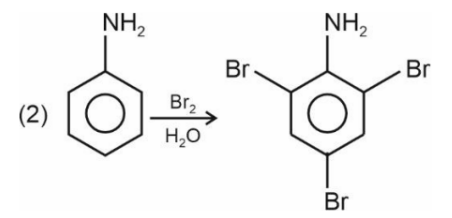
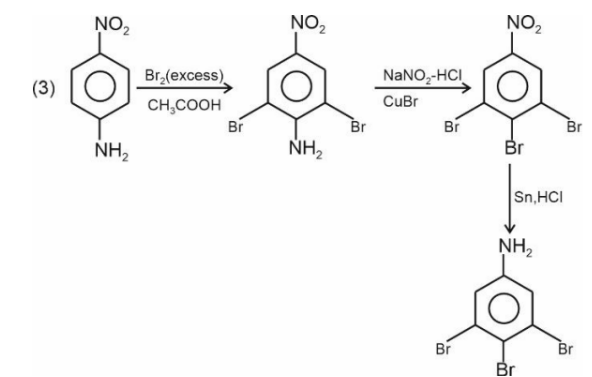
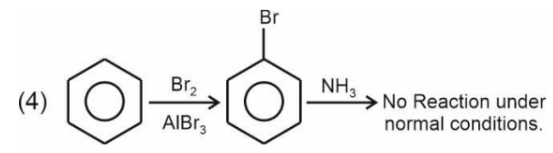
Hence, the correct answer is option (3).
|
Daily PDF |
Full Length Test: Mathematics test paper prepared as per the JEE Main pattern. It is designed to help students assess their overall understanding and exam readiness in Mathematics.
|
Full Length Test |
Electronic Device: Logic Gates is a frequently asked concept of this chapter
Question: The output (Y) of logic circuit given below is 0 only when :

1) $A=1, B=0$
2) (correct)$A=0, B=0$
3) $A=1, B=1$
4) $A=0, B=1$
Solution:
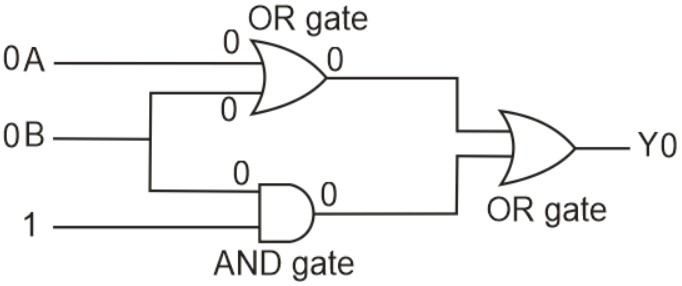
Hence, the answer is the option 2.
|
Daily PDF |
Chemistry
d - and f - BLOCK ELEMENTS: Magnetic Properties and Character is the scoring topic of this chapter.
Question: Consider ' $n$ ' is the number of lone pair of electrons present in the equatorial position of the most stable structure of $\mathrm{ClF}_3$. The ions from the following with ' $n$ ' number of unpaired electrons are:
A. $\mathrm{V}^{3+}$
B. $\mathrm{Ti}^{3+}$
C. $\mathrm{Cu}^{2+}$
D. $\mathrm{Ni}^{2+}$
E. $\mathrm{Ti}^{2+}$
Choose the correct answer from the options given below :
1) A and C only
2) (correct) A, D and E only
3) B and C only
4) B and D only
Solution:
$\mathrm{ClF}_3$
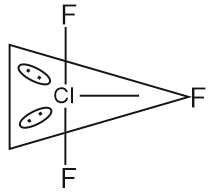
$\mathrm{n}=2$ (No of lone pair present in equitorial plane)
(Unpaired e )
(A) $\mathrm{V}^{+3}:[\mathrm{Ar}] 3 \mathrm{~d}^2$ 2
(B)$\mathrm{Ti}^{31}:[\mathrm{Ar}] 3 \mathrm{~d}^1$ 1
(C) $\mathrm{Cu}^{+2}:[\mathrm{Ar}] 3 \mathrm{~d}^9$ 1
(D) $\mathrm{Ni}^{12}:[\mathrm{Ar}] 3 \mathrm{~d}^8$ 2
(E)$\mathrm{Ti}^{+3}:[\mathrm{Ar}] 3 \mathrm{~d}^2$ 2
Hence, the correct answer is option (2).
|
Daily PDF |
Among top 100 Universities Globally in the Times Higher Education (THE) Interdisciplinary Science Rankings 2026
Last Date to Apply: 28th Feb | Ranked #43 among Engineering colleges in India by NIRF | Highest Package 1.3 CR , 100% Placements
Differential equations: Linear Differential Equation are the scoring topics of this chapter.
Question: Let $y=y(x)$ be the solution of the differential equation $\frac{d y}{d x}+3\left(\tan ^2 x\right) y+3 y=\sec ^2 x, y(0)=\frac{1}{3}+e^3$. Then $y\left(\frac{\pi}{4}\right)$ is equal to
1) $\frac{2}{3}$
2) (correct)$\frac{4}{3}$
3) $\frac{4}{3}+e^3$
4) $\frac{2}{3}+\mathrm{e}^3$
Solution:
We have the differential equation,
$\begin{array}{l}\frac{d y}{d x}+3\left(\tan ^2 x\right) y+3 y=\sec ^2 x \\ \Rightarrow \frac{d y}{d x}+3 \sec ^2 x y=\sec ^2 x\end{array} $
Compare it with the linear differential equation,
$\frac{dy}{dx}+Py=Q$
We get, $Q=\sec^2 x$
Use this in the formula,
$I.F =e^{\int Pd x}$
$I.F =e^{\int 3 \sec ^2 x d x}$
$\quad=e^{3 \tan x}$
The solution to the differential equation is given by:
$y \cdot e^{3\tan x}=\int e^{3 \tan x} \cdot \sec ^2 x d x+c$
$y \cdot e^{3 \tan x}=\frac{e^{3 \tan x}}{3}+c$
$\begin{aligned} & \text { Also } f(0)=\frac{1}{3}+e^3 \\ & \Rightarrow\left(\frac{1}{3}+e^3\right)=\frac{1}{3}+c \\ & \Rightarrow c=e^3 \\ & \therefore y \cdot e^{3 \tan x}=\frac{e^{3 \tan x}}{3}+e^3 \\ & \text { Put } x=\frac{\pi}{4} \\ & y e^3=\frac{e^3}{3}+e^3 \Rightarrow y=\frac{4}{3}\end{aligned}$
Hence, the correct answer is option (2).
|
Daily PDF |
Day 26 focuses on the full Mock Test to analyse your preparation and accuracy. It helps identify strengths and weak areas for smarter improvement.
|
Mock Test |
Kinetic Theory of Gases: Mayer's formula is a frequently asked concept of this chapter
Question: For a diatomic gas, if $\gamma_1=\left(\frac{C p}{C v}\right)$ for rigid molecules and $\gamma_2=\left(\frac{\mathrm{Cp}_{\mathrm{p}}}{\mathrm{Cv}}\right)$ for another diatomic molecule, but also having vibrational modes. Then, which one of the following options is correct?
( Cp and Cv are specific heats of the gas at constant pressure and volume)
1) $\gamma_2>\gamma_1$
2) $\gamma_2=\gamma_1$
3)$2 \gamma_2=\gamma_1$
4) (correct) $\gamma_2<\gamma_1$
Solution:
For a Rigid diatomic molecule, the degree of freedom $f_1=5$
$
\Rightarrow \gamma_1=1+\frac{2}{f_1}= 1+\frac{2}{5}=\frac{7}{5}
$
For a diatomic molecule with a vibrational mode,the degree of freedom
$
\begin{aligned}
& f_2=7 . \\
& \Rightarrow \gamma_2=1+\frac{2}{7}=\frac{9}{7}. \\
& \Rightarrow \gamma_1>\gamma_2
\end{aligned}
$
Hence, the answer is option (4).
|
Daily PDF |
Recognized as Institute of Eminence by Govt. of India | NAAC ‘A++’ Grade | Upto 75% Scholarships
98% Placement Record | Highest CTC 81.25 LPA | NAAC A++ Accredited | Ranked #62 in India by NIRF Ranking 2025 | JEE & JET Scores Accepted
Classification of Elements and Periodic Table: Ionisation Enthalpy or Ionisation Potential is the scoring topic of this chapter.
Question: The successive 5 ionisation energies of an element are $800,2427,3658,25024$ and $32824 \mathrm{~kJ} / \mathrm{mol}$, respectively. By using the above values predict the group in which the above element is present:
1) Group 2
2) (correct) Group 13
3) Group 4
4) Group 14
Solution:
The $\mathrm{IE}_4$ is suddenly very high therefore element must have 3 valence $\mathrm{e}^{-}(\mathrm{s})$ and it belong to group 13
Hence, the correct answer is option (2).
Permutations and combinations: APPLICATION OF PERMUTATION-VI are the scoring topics of this chapter.
Question: The number of 3-digit numbers that are divisible by 2 and 3 , but not divisible by 4 and 9, is
Solution:
We are given the task to find how many 3-digit numbers are divisible by both $2$ and $3$, but not divisible by both $4$ and $9$.
First, compute the total number of 3-digit numbers. The smallest 3-digit number is $100$, and the largest is $999$, so:
$
999 - 99 = 900
$
Now, numbers divisible by both $2$ and $3$ are divisible by their LCM:
$
\text{LCM}(2, 3) = 6
$
So, the number of 3-digit numbers divisible by $6$ is:
$
\frac{900}{6} = 150
$
Next, consider numbers divisible by both $4$ and $9$. Their LCM is:
$
\text{LCM}(4, 9) = 36
$
So, the number of 3-digit numbers divisible by $36$ is:
$
\frac{900}{36} = 25
$
Hence, the number of 3-digit numbers divisible by $2$ and $3$ but not by $4$ and $9$ is:
$
150 - 25 = 125
$
Hence, the answer is 125.
|
Daily PDF |
Work, Energy, and Power: The Conservation of Energy is the frequently asked concept of this chapter
Question: A particle is released from height $S$ above the surface of the earth. At certain height its kinetic energy is three times its potential energy. The height from the surface of the earth and the speed of the particle at that instant are respectively:
1) $\frac{\mathrm{S}}{2}, \sqrt{\frac{3 \mathrm{gS}}{2}}$
2) $\frac{\mathrm{S}}{2}, \frac{3 \mathrm{gS}}{2}$
3) $\frac{\mathrm{S}}{4}, \frac{3 \mathrm{gS}}{2}$
4) (correct) $\frac{\mathrm{S}}{4}, \sqrt{\frac{3 \mathrm{gS}}{2}}$
Solution:
Let, the required height of body is y.
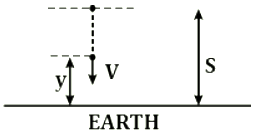
When body from rest falls through height ( $S-\mathrm{y}$ ). Then under constant acceleration,
$
\begin{aligned}
& v^2=0^2+2 g(S-y) \\
& v=\sqrt{ } 2 g(S-y)
\end{aligned}
$
When the body is at height $y$ above the ground. Potential energy of body of mass $m$,
$
\mathrm{U}=\mathrm{mgy}
$
As per given condition kinetic energy, $\mathrm{K}=3 \mathrm{U}$
$
\Rightarrow \frac{1}{2} m(v)^2=3 \times m g(y)
$
Using equations (1) and (2),
$
\begin{aligned}
& \Rightarrow \mathrm{S}-\mathrm{y}=3 \mathrm{y} \\
& \therefore \mathrm{y}=\frac{S}{4}
\end{aligned}
$
From (1),
$
\begin{aligned}
& v=\sqrt{2 \times g\left(S-\frac{S}{4}\right)} \\
& =\sqrt{\frac{3 g S}{2}}
\end{aligned}
$
Hence, the answer is the option (4).
|
Daily PDF |
Biomolecules: Carbohydrate is the scoring topic of this chapter.
Question:
Identify the number of structure/s from the following
which can be correlated to D-glyceraldehyde.
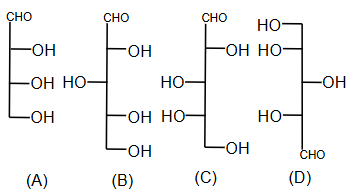
1) Three
2) two
3) four
4) one
Solution:

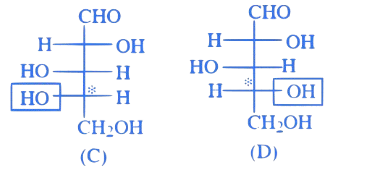
D-glucose: The OH on the penultimate carbon points right.
In $\mathrm{A}, \mathrm{B}, \mathrm{D}-\mathrm{OH}$ group in right-hand side then D-configuration is assigned.
Hence, the correct answer is option (1).
|
Daily PDF |
Three-Dimensional Geometry: Equations for a Line in Space are the scoring topics of this chapter.
Question: The distance of the line $\frac{x-2}{2}=\frac{y-6}{3}=\frac{z-3}{4}$ from the point $(1,4,0)$ along the line $\frac{x}{1}=\frac{y-2}{2}=\frac{z+3}{3}$ is:
1) $\sqrt{17}$
2) (correct) $\sqrt{14}$
3) $\sqrt{15}$
4) $\sqrt{13}$
Solution: Let the equation of the line parallel to the given one and passing through point $ (1, 4, 0) $ be:
$
\frac{x - 1}{1} = \frac{y - 4}{2} = \frac{z - 0}{3}
$
Let this line intersect the given line:
$
x = 2t + 2,\quad y = 3t + 6,\quad z = 4t + 3
$
Assume the point of intersection lies on both lines. From the parametric form of the first line, let the point be:
$
(x, y, z) = (\lambda + 1, 2\lambda + 4, 3\lambda)
$
Now equate with the coordinates from the second line:
$
\lambda + 1 = 2t + 2 \Rightarrow \lambda = 2t + 1 \quad \text{(1)}
$
$
2\lambda + 4 = 3t + 6 \quad \text{(2)}
$
Substitute equation (1) into equation (2):
$
2(2t + 1) + 4 = 3t + 6 \Rightarrow 4t + 2 + 4 = 3t + 6 \Rightarrow t = 0
$
Using $ t = 0 $ in the second line’s equations:
$
x = 2(0) + 2 = 2,\quad y = 3(0) + 6 = 6,\quad z = 4(0) + 3 = 3
$
So, the point of intersection is $ (2, 6, 3) $
Now, find the distance between the point $ (1, 4, 0) $ and $ (2, 6, 3) $:
$
\text{Distance} = \sqrt{(2 - 1)^2 + (6 - 4)^2 + (3 - 0)^2}
= \sqrt{1 + 4 + 9} = \sqrt{14}
$
Hence, the correct answer is Option (2).
|
Daily PDF |
Electromagnetic Induction and Alternating Currents: Root mean square (RMS) value is the frequently asked concept of this chapter
Question: An alternating current is given by $\mathrm{I}=\mathrm{I}_{\mathrm{A}} \sin \omega \mathrm{t}+\mathrm{I}_{\mathrm{B}} \cos \omega \mathrm{t}$.
The r.m.s. current will be :-
1) $\sqrt{\mathrm{I}_{\mathrm{A}}^2+\mathrm{I}_{\mathrm{B}}^2}$
2) $\frac{\sqrt{I_A^2+I_B^2}}{2}$
3) (correct) $\sqrt{\frac{\mathrm{I}_{\mathrm{A}}^2+\mathrm{I}_{\mathrm{B}}^2}{2}}$
4) $\frac{\left|I_A+I_B\right|}{\sqrt{2}}$
Solution:
$\begin{aligned}
&\begin{aligned}
I=I_A \sin \omega t & +I_B \cos \omega t \\
I^2=I_A^2 \sin ^2 \omega t & +I_B^2 \cos ^2 \omega t +I_A I_B \sin 2 \omega t
\end{aligned}\\
&\begin{aligned}
I_{m \rho}= & I_A{ }^2 \cdot\left\langle\sin ^2 \omega t\right\rangle+I_B{ }^2 \cdot\left\langle\cos ^2 \omega t\right\rangle +I_A I_B \cdot\langle\sin 2 \omega t\rangle \\
= & \frac{I_A{ }^2}{2}+\frac{I_B{ }^2}{2}+0 \Rightarrow I_{rms}=\sqrt{\frac{I_A{ }^2+I_B{ }^2}{2}} .
\end{aligned}
\end{aligned}$
Hence, the answer is the option (3).
Atomic Structure: Photoelectric effect is the scoring topic of this chapter.
Question:

Which of the following statements are correct, if the threshold frequency of caesium is $5.16 \times 10^{14} \mathrm{~Hz}$ ?
A. When Cs is placed inside a vacuum chamber with an ammeter connected to it and yellow light is focused on Cs the ammeter shows the presence of current.
B. When the brightness of the yellow light is dimmed, the value of the current in the ammeter is reduced.
C. When a red light is used instead to the yellow light, the current produced is higher with respect to the yellow light.
D. When a blue light is used, the ammeter shows the formation of current.
E. When a white light is used, the ammeter shows formation of current.
Choose the correct answer from the options given below :
1) A, D and E Only
2) B, C and D Only
3) A, C, D and E Only
4) (correct) $\mathrm{A}, \mathrm{B}, \mathrm{D}$ and E Only
Solution:
$\begin{aligned} & \lambda=\frac{\mathrm{C}}{\mathrm{v}}=\frac{3 \times 10}{5.16 \times 10^{14}} \\ & \lambda=581.39 \mathrm{~nm}\end{aligned}$
* $\lambda_{\text {Photon }}$ is near $\&$ below yellow light it can show photoelectric effect.
* If intensity of light decreases photocurrent decreases.
* Red light will not produce photoelectric effect.
* $v_{\text {Blue }}>v_{\text {yellow }}$ so photoelectric current will be produced.
* White light contain all frequencies so it will show photo electric current.
Correct statements are $\mathrm{ABD} \& \mathrm{E}$.
Hence, the correct answer is option (4).
|
Daily PDF |
Permutations and combinations: APPLICATIONS OF SELECTIONS -I are the scoring topics of this chapter.
Question: The number of ways, in which the letters $\mathrm{A}, \mathrm{B}, \mathrm{C}$, $D$, $E$ can be placed in the 8 boxes of the figure below so that no row remains empty and at most one letter can be placed in a box, is :
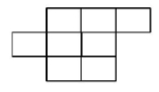
1) 5880
2) 960
3) 840
4) (correct) 5760
Solution:
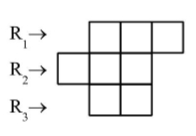
Given the row-wise availability:
R₁: 3 1 2 2 1
R₂: 1 3 2 1 2
R₃: 1 1 1 2 2
Required number of ways:
$\left(
^{3}C_{3} .^{3}C_{1} .^{2}C_{1}
+
^{3}C_{1} .^{3}C_{3} .^{2}C_{1}
+
^{3}C_{2} .^{3}C_{2}. ^{2}C_{1}
+
^{3}C_{2}. ^{3}C_{1}.^{3}C_{2}
+
^{3}C_{1} .^{3}C_{2}. ^{2}C_{2}
\right) \times 5!$
$= (12 + 18 + 9 + 9) \times 120 = 48 \times 120 = 5760$
The number of ways$=5760$
Hence, the answer is option (4).
|
Daily PDF |
Dual Nature of Matter and Radiation: Einstein's Photoelectric equation is the frequently asked concept of this chapter
Question: A light source of wavelength $\lambda$ illuminates a metal surface, and electrons are ejected with maximum kinetic energy of 2 eV. If the same surface is illuminated by a light source of wavelength $\frac{\lambda}{2}$, then the maximum kinetic energy of ejected electrons will be (The work function of metal is 1 eV ):
1) 2 eV
2) 6 eV
3) (correct) 5 eV
4) 3 eV
Solution:
$\begin{aligned} & \mathrm{E}^{\prime}=\frac{\mathrm{hC}}{\lambda} \\ & \mathrm{K}=\mathrm{E}-\phi=2 \mathrm{eV} \\ & \mathrm{E}-1=2 \\ & \mathrm{E}=3 \mathrm{eV}\end{aligned}$ $\begin{aligned} & \mathrm{E}^{\prime}=\frac{\mathrm{hC}}{\lambda / 2}=2 \mathrm{E} \\ & \mathrm{K}^{\prime}=2 \mathrm{E}-\phi \\ & =2[3 \mathrm{ev}]-1 \mathrm{eV} \\ & =(6-1) \mathrm{ev}=5 \mathrm{eV}\end{aligned}$
Hence, the answer is option (3).
|
Daily PDF |
Some Basic Principles of Organic Chemistry: IUPAC is the scoring topic of this chapter.
Question: The IUPAC name of the following compound is
1) 2-Carboxy-5-methoxycarbonylhexane.
2) Methyl-6-carboxy-2,5-dimethylhexanoate
3) Methyl-5-carboxy-2-methylhexanoate.
4) 6-Methoxycarbonyl-2,5-dimethylhexanoic acid.
Solution:
The parent chain will be the one containing the maximum number of carbons and containing carboxylic acid. Based on this, the number will be assigned to the other groups. The parent chain will be an acid, not an ester, as acid gets priority over ester.
So, IUPAC name will be 6-methoxycarbonyl-2,5-dimethylhexanoic acid.
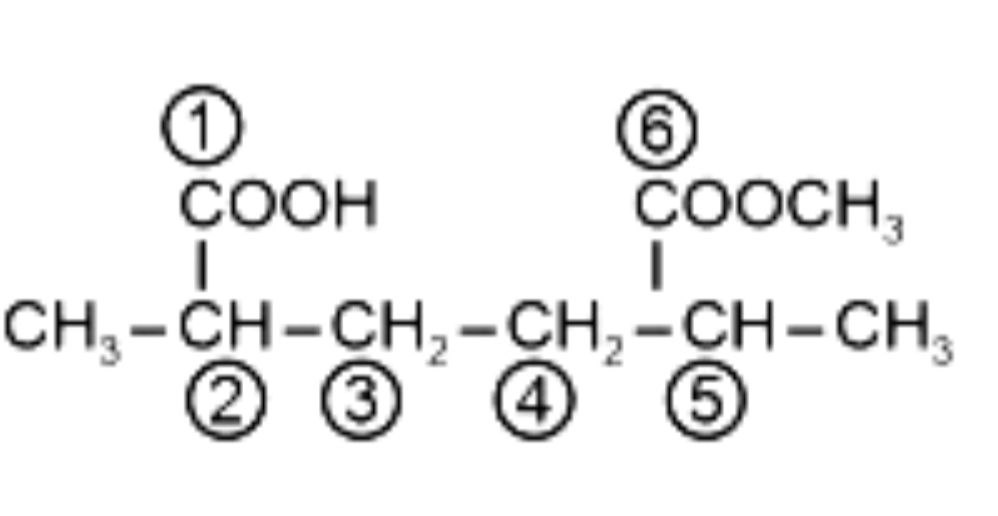
6-Methoxycarbonyl-2,5-dimethylhexanoic acid.
Hence, the correct answer is option (4).
Binomial theorem and its simple applications: Binomial Theorem and Expression of Binomial Theorem are the scoring topics of this chapter.
Question: If $\sum_{\mathrm{r}=1}^{30} \frac{\mathrm{r}^2\left({ }^{30} \mathrm{C}_{\mathrm{r}}\right)^2}{{ }^{30} \mathrm{C}_{\mathrm{r}-1}}=\alpha \times 2^{29}$, then $\alpha$ is equal to $\_\_\_\_$ .
Solution:
Given,$\displaystyle\sum_{r=1}^{30} \frac{r^2 \binom{30}{r}^2}{\binom{30}{r-1}}$
Simplify the ratio of binomial coefficients:
$
\frac{\binom{30}{r}}{\binom{30}{r-1}} = \frac{30 - r + 1}{r} = \frac{31 - r}{r}
$
Rewrite the sum as:
$
\displaystyle\sum_{r=1}^{30} r^2 \left(\frac{31 - r}{r}\right) \binom{30}{r} $
$= \displaystyle\sum_{r=1}^{30} (31 - r) r \binom{30}{r}$
$
=\displaystyle\sum_{r=1}^{30} (31 - r) r \frac{30!}{r! (30 - r)!} $ ($\binom{30}{r} = \frac{30!}{r! (30 - r)!}$)
$= \displaystyle\sum_{r=1}^{30} (31 - r) \frac{30!}{(r-1)! (30 - r)!}$
$
= 30 \displaystyle\sum_{r=1}^{30} (31 - r) \frac{29!}{(r-1)! (30 - r)!}
$
Recognize the binomial coefficient $\binom{29}{k}$:
$
\frac{29!}{k! (29 - k)!} = \binom{29}{k}
$
By substituting $k = 30 - r$, the sum becomes:
$
30 \displaystyle\sum_{r=1}^{30} (31 - r) \binom{29}{30 - r}
$
Split the sum into two parts:
$
30 \left( \displaystyle\sum_{r=1}^{30} (31 - r) \binom{29}{30 - r} \right) = 30 \left( \displaystyle\sum_{k=0}^{29} (k+1) \binom{29}{k} \right)
$
Use the standard binomial identities:
$
\displaystyle\sum_{k=0}^n \binom{n}{k} = 2^n
$
$
\displaystyle\sum_{k=0}^n k \binom{n}{k} = n 2^{n-1}
$
Calculate the sum:
$
\displaystyle\sum_{k=0}^{29} (k+1) \binom{29}{k} = \displaystyle\sum_{k=0}^{29} k \binom{29}{k} + \displaystyle\sum_{k=0}^{29} \binom{29}{k} = 29 \cdot 2^{28} + 2^{29} = (29 + 2) 2^{28} = 31 \cdot 2^{28}
$
Therefore, the original sum evaluates to:
$
30 \times 31 \times 2^{28} = 15 \times 31 \times 2^{29} = 465 \times 2^{29}
$
Hence, the value of $\alpha$ is $465$
Day 21 focus on full Mock Test to analyse your preparation and accuracy. It helps identify strengths and weak areas for smarter improvement.
| Mock Test | Mock Test 3 |
Thermodynamics: Isothermal Process is the frequently asked concept of this chapter
Question:
A poly-atomic molecule $\left(\mathrm{C}_{\mathrm{v}}=3 \mathrm{R}, \mathrm{C}_{\mathrm{P}}=4 \mathrm{R}\right.$, where $R$ is gas constant) goes from phase space point $\mathrm{A}\left(\mathrm{P}_{\mathrm{A}}=10^5 \mathrm{~Pa}, \mathrm{~V}_{\mathrm{A}}=4 \times 10^{-6} \mathrm{~m}^3\right)$ to point $\mathrm{B}\left(\mathrm{P}_{\mathrm{B}}=5\right.$ $\left.\times 10^4 \mathrm{~Pa}, \mathrm{~V}_{\mathrm{B}}=6 \times 10^{-6} \mathrm{~m}^3\right)$ to point $\mathrm{C}\left(\mathrm{P}_{\mathrm{C}}=10^4 \mathrm{~Pa}\right.$, $\mathrm{V}_{\mathrm{C}}=8 \times 10^6 \mathrm{~m}^3$ ). A to B is an adiabatic path, and B to C is an isothermal path.
The net heat absorbed per unit mole by the system is :
1)
$500 \mathrm{R}(\ln 3+\ln 4)$
2) (correct)
$450 \mathrm{R}(\ln 4-\ln 3)$
3)
$500 \mathrm{R} \ln 2$
4)
$400 \mathrm{R} \ln 4$
Solution:
As $A$ to $B$ is can adiabatic path,
So, $\Delta Q_{A \rightarrow B}=0 \quad \cdots (1)$
So, now we need to find the heat absorbed for the isothermal path (B to C)
We know, a change in internal energy
$
\begin{aligned}
& \Delta U=m c_v \Delta T \\
& \Rightarrow \Delta U= 0(\text { for isothermal as } \Delta T=0)
\end{aligned}
$
Now, using 1st law of thermodynamics.
$
\begin{aligned}
& \Delta Q=\Delta U+W \\
& \Rightarrow \Delta Q= 0+W \Rightarrow \Delta Q=w
\end{aligned}
$
So,
$
\begin{aligned}
& \Delta Q_{B \rightarrow C} =W_{B \rightarrow C} \\
\Rightarrow & \Delta Q_{B \rightarrow C} =n R T \ln \left(\frac{v_C}{v_B}\right) \\
\Rightarrow & \Delta Q_{B \rightarrow C}=n R(450) \ln \left(\frac{4}{3}\right) \\
\Rightarrow & \Delta Q_{B \rightarrow C}=450 n R \ln \left(\frac{4}{3}\right) \quad \cdots (2)
\end{aligned}
$
So net heat absorbed,
$
\begin{aligned}
& Q=\Delta Q_{A \rightarrow B}+\Delta Q_{B \rightarrow C} \\
& \Rightarrow Q=450 n R \ln \left(\frac{4}{3}\right) \ldots(\text { from } 1 \text { and } 2)
\end{aligned}
$
Net heat absorbed per mole,
$
\Rightarrow \frac{Q}{n}=450 R(\ln 4-\ln 3)
$
Hence, the answer is option (2).
|
Daily PDF |
Organic Compounds containing Halogens: Elimination-Addition Mechanism(I) is the scoring topic of this chapter.
Question: Which one of the following reactions will not lead to the desired ether formation in a major proportion? (iso- $\mathrm{Bu} \Rightarrow$ isobutyl, sec- $\mathrm{Bu} \Rightarrow$ sec-butyl, $\mathrm{nPr} \Rightarrow$ n-propyl, ${ }^{\text {' } \mathrm{Bu}} \Rightarrow$ tert-butyl, $\mathrm{Et} \Rightarrow$ ethyl)
1) ${ }^{\prime} \mathrm{BuO} \stackrel{\ominus}{\mathrm{N}} \mathrm{a}+\mathrm{EtBr} \rightarrow{ }^{\mathrm{t}} \mathrm{Bu}-\mathrm{O}-\mathrm{Et}$
2)
3)
4) iso- $\mathrm{BuO} \stackrel{\ominus}{\mathrm{N}} \mathrm{a}+\mathrm{sec}-\mathrm{BuBr} \rightarrow \mathrm{Sec}-\mathrm{Bu}-\mathrm{O}-\mathrm{iso}-\mathrm{Bu}$
Solution:
For $2^{\circ} \mathrm{RX} \Rightarrow$ elimination would be more favourable than substitution
Primary alkyl halide undergoes Williamson's synthesis for the formation of ether
$\mathrm{RO}^{\ominus} \mathrm{Na}^{+}+\mathrm{RX} \rightarrow \mathrm{ROR}$ (undergo $\mathrm{S}_{\mathrm{N}} 2$ reaction)
(where RX = Primary alkyl halide)
Hence, the correct answer is option (4).
|
Daily PDF |
Binomial theorem and its simple applications: Series Involving Binomial Coefficients is the scoring topic of this chapter.
Question: If $\sum_{\mathrm{r}=0}^{10}\left(\frac{10^{\mathrm{r}+1}-1}{10^{\mathrm{r}}}\right) \cdot{ }^{11} \mathrm{C}_{\mathrm{r}+1}=\frac{\alpha^{11}-11^{11}}{10^{10}}$, then $\alpha$ is equal to:
1) 15
2) 11
3) 24
4) 20
Solution:
Given:
$\sum_{r=0}^{10} \left(\frac{10^{r+1} - 1}{10^r}\right) \cdot {}^{11}\mathrm{C}_{r+1} = \frac{\alpha^{11} - 11^{11}}{10^{10}}$
Simplify the term inside the sum:
$\frac{10^{r+1} - 1}{10^r} = \frac{10 \cdot 10^r - 1}{10^r} = 10 - \frac{1}{10^r}$
Rewrite the sum:
$\sum_{r=0}^{10} \left(10 - \frac{1}{10^r}\right) \cdot \binom{11}{r+1} = \sum_{r=0}^{10} 10 \cdot \binom{11}{r+1} - \sum_{r=0}^{10} \frac{1}{10^r} \cdot \binom{11}{r+1}$
Changing the index $k = r+1$, $k$ goes from 1 to 11:
\[
\sum_{r=0}^{10} \binom{11}{r+1} = \sum_{k=1}^{11} \binom{11}{k} = 2^{11} - 1 = 2047
\]
Substitute:
$= 10 \times 2047 - \sum_{r=0}^{10} \frac{1}{10^r} \cdot {}^{11}\mathrm{C}_{r+1}$
Use the binomial expansion:
$(1 + x)^{11} = \sum_{k=0}^{11} {}^{11}\mathrm{C}_k \cdot x^k$
Putting $x = \frac{1}{10}$:
$\left(1 + \frac{1}{10}\right)^{11} = \sum_{k=0}^{11} {}^{11}\mathrm{C}_k \cdot 10^{-k}$
Rewrite the sum inside subtraction:
\[
\sum_{r=0}^{10} \frac{1}{10^r} \cdot {}^{11}C_{r+1}
= \sum_{k=1}^{11} {}^{11}C_k \cdot 10^{-(k-1)}
= 10 \sum_{k=1}^{11} {}^{11}C_k \cdot 10^{-k}
\]
This equals:
$10 \left( \sum_{k=0}^{11} {}^{11}\mathrm{C}_k \cdot 10^{-k} - 1 \right) = 10 \left( \left(1 + \frac{1}{10}\right)^{11} - 1 \right)$
Simplify:
$10 \left( \left(\frac{11}{10}\right)^{11} - 1 \right)$
Substitute back:
$\sum_{r=0}^{10} \left(\frac{10^{r+1} - 1}{10^r}\right) \cdot {}^{11}\mathrm{C}_{r+1} = 10 \times 2047 - 10 \left(\left(\frac{11}{10}\right)^{11} - 1\right) = 10 \times 2047 - 10 \left(\frac{11}{10}\right)^{11} + 10$
$= 10 \times 2048 - 10 \left(\frac{11}{10}\right)^{11}$
Recall the original equation:
$\frac{\alpha^{11} - 11^{11}}{10^{10}} = 10 \times 2048 - 10 \left(\frac{11}{10}\right)^{11}$
Multiply both sides by $10^{10}$:
$\alpha^{11} - 11^{11} = 10^{11} \times 2048 - 10^{11} \times \left(\frac{11}{10}\right)^{11}$
Simplify the right side:
$= 2048 \times 10^{11} - 11^{11}$
Rearranged:
$\alpha^{11} = 2048 \times 10^{11}$
Since $2048 = 2^{11}$,
$\alpha^{11} = 2^{11} \times 10^{11} = (2 \times 10)^{11} = 20^{11}$
Taking the 11th root:
$\alpha = 20$
Hence, the correct answer is option (4).
Thermodynamics: Adiabatic process is the frequently asked concept of this chapter
Question: In an adiabatic process, which of the following statements is true?
1) The molar heat capacity is infinite
2) Work done by the gas equals the increase in internal energy
3) (correct) The molar heat capacity is zero
4) The internal energy of the gas decreases as the temperature increases
Solution:
For adiabatic process, $\mathrm{dQ}=0$
∴ Molar heat capacity $=0$
$\because \mathrm{dQ}=0 \Rightarrow \mathrm{dU}=-\mathrm{dW}$
Also $\mathrm{dU}=\frac{\mathrm{f}}{2} \mathrm{nRdT}$
Hence, the answer is the option (3).
|
Daily PDF |
Some basic concepts in chemistry: Mole Concept And Molar Mass is the scoring topic of this chapter.
Question: Xg of benzoic acid on reaction with aq. $\mathrm{NaHCO}_3$ release $\mathrm{CO}_2$ that occupied 11.2 L volume at STP. X is $\_\_\_\_$ g.
Solution:
$\begin{aligned} & \mathrm{C}_6 \mathrm{H}_5 \mathrm{COOH}+\mathrm{NaHCO}_3 \rightarrow \mathrm{C}_6 \mathrm{H}_5 \mathrm{COO}^{-} \mathrm{Na}^{+} \ +\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2 \\ & x \mathrm{gm} \\ & \text { mole of } \mathrm{C}_6 \mathrm{H}_5 \mathrm{COOH}=\text { mole of } \mathrm{CO}_2=\frac{11.2}{22.4}=0.5 \\ & \text { mass of } \mathrm{C}_6 \mathrm{H}_5 \mathrm{COOH}=x=0.5 \times 122=61 \mathrm{gm}\end{aligned}$
Hence, the answer is (61)
|
Daily PDF |
Sequence and series: Sum of n terms of an AP is the scoring topic of this chapter.
Question: Let $\mathrm{a}_1, \mathrm{a}_2, \ldots, \mathrm{a}_{2024}$ be an Arithmetic Progression such that $a_1+\left(a_5+a_{10}+a_{15}+\ldots+a_{2020}\right)+a_{2024}=2233$. Then $a_1+a_2+a_3+\ldots+a_{2024}$ is equal to $\_\_\_\_$ .
The terms $ a_5 + a_{10} + a_{15} + \ldots + a_{2020} $ form an arithmetic sub-sequence of the original A.P., with a common difference of 5.
First term of this sub-sequence: $ a_5 $
Last term: $ a_{2020} $
Common difference: 5
Total terms: $ \frac{2020 - 5}{5} + 1 = \frac{2015}{5} + 1 = 403 + 1 = 404 $
So the given equation becomes:
$
a_1 + (a_5 + a_{10} + \ldots + a_{2020}) + a_{2024} = 2233.
$
Let’s observe that in an arithmetic progression, the sum of terms equidistant from the beginning and the end is constant:
$
a_1 + a_{2024} = a_5 + a_{2020} = a_{10} + a_{2015} = \ldots
$
So, we can pair $ a_1 + a_{2024} $ and 202 terms from the sub-sequence as 202 pairs of the form $ a_k + a_{2025-k} $. Therefore:
$
\text{Total pairs} = 1 (\text{from }a_1 + a_{2024}) + 202 = 203.
$
Let this common pair sum be $ S = a_1 + a_{2024} $. Then:
$
203 \cdot S = 2233 \Rightarrow S = \frac{2233}{203} = 11.
$
Now, to find the sum $ a_1 + a_2 + \ldots + a_{2024} $, we use the standard A.P. sum formula:
$
S_{2024} = \frac{2024}{2}(a_1 + a_{2024}) = 1012 \cdot 11 = 11132.
$
Hence, the answer is 11132.
|
Daily PDF |
Physics and Measurement: Application of Dimensional Analysis (V)- As a research tool to derive new relations is the frequently asked concept of this chapter
Question: In an electromagnetic system, the quantity representing the ratio of electric flux and magnetic flux has the dimension of $\mathrm{M}^{\mathrm{P}} \mathrm{L}^{\mathrm{Q}} \mathrm{T}^{\mathrm{R}} \mathrm{A}^{\mathrm{S}}$, where values of ' $Q$ ' and ' $R$ ' are
1) $(3,-5)$
2) $(-2,2)$
3) $(-2,1)$
4) (correct) $(1,-1)$
Solution:
Electric flux is defined as
$
\Phi_E=\int_S \mathbf{E} \cdot d \mathbf{A}
$
The electric field $\mathbf{E}$ has dimensions:
$
[E]=\frac{\text { Force }}{\text { Charge }} .
$
Since force has dimensions $M L T^{-2}$, and charge (in Sl) has dimensions $A T$, we get:
$
[E]=\frac{M L T^{-2}}{A T}=M L T^{-3} A^{-1}
$
The area element $d A$ has dimensions $L^2$.
Thus, the electric flux has dimensions:
$
\left[\Phi_E\right]=[E][A]=M L T^{-3} A^{-1} \times L^2=M L^3 T^{-3} A^{-1}
$
Magnetic flux is defined as
$
\Phi_B=\int_S \mathbf{B} \cdot d \mathbf{A}
$
The magnetic field $\mathbf{B}$ has dimensions determined via the Lorentz force law (using $F=q v B$ ), giving:
$
[B]=\frac{F}{q v}=\frac{M L T^{-2}}{(A T)\left(L T^{-1}\right)}=M T^{-2} A^{-1}
$
Again, the area element has dimensions $L^2$.
So the magnetic flux has dimensions:
$
\left[\Phi_B\right]=[B][A]=\left(M T^{-2} A^{-1}\right)\left(L^2\right)=M L^2 T^{-2} A^{-1}
$
Taking the ratio:
$
\frac{\Phi_E}{\Phi_B}=\frac{M L^3 T^{-3} A^{-1}}{M L^2 T^{-2} A^{-1}}
$
Canceling like terms:
Mass ( $M$ ) cancels.
Current $\left(A^{-1}\right)$ cancels.
For length, $L^{3-2}=L^1$.
For time, $T^{-3-(-2)}=T^{-1}$.
Therefore, the ratio has dimensions:
$
L^1 T^{-1}
$
This means in the expression
$
M^P L^Q T^R A^S,
$
the exponents for length and time are $Q=1$ and $R=-1$.
Hence, the answer is option (4).
|
Daily PDF |
Chemical kinetics: First-order reaction is the scoring topic of this chapter.
Question: $\mathrm{A}(\mathrm{g}) \rightarrow \mathrm{B}(\mathrm{g})+\mathrm{C}(\mathrm{g})$ is a first order reaction.
| Time | T | $\infty$ |
| $\mathbf{P}_{\text {system }}$ | $\mathrm{P}_{\mathrm{t}}$ | $\mathrm{P}_{\infty}$ |
The reaction was started with reactant A only. Which of the following expressions is correct for the rate constant k?
Solution:
$\mathrm{A}(\mathrm{g}) \rightarrow \mathrm{B}(\mathrm{g})+\mathrm{C}(\mathrm{g})$
$\begin{array}{ccccc} & \\ \mathrm{t}=0 & \mathrm{p}_0 & & 0 & 0 \\ \mathrm{t}=\mathrm{t} & \mathrm{p}_0-\mathrm{p} & & \mathrm{p} & \mathrm{p} \\ \mathrm{t}=\infty & 0 & & p_0 & p_0\end{array}$
$\begin{array}{ll}\text { At } \begin{aligned} t & =t \\ t & =\infty\end{aligned} \quad \begin{array}{l}p_t=p_0+p \\ 2 p_0=p_{\infty}\end{array}\end{array}$
For first-order reaction
$\begin{array}{ll}k=\frac{1}{t} \ln \frac{\left(p_0\right)_A}{\left(p_t\right)_A} & p_0-p=\frac{p_{\infty}}{2}-p_t+\frac{p_{\infty}}{2} \\ =\frac{1}{t} \ln \frac{p_0}{p_0-p} & =p_{\infty}-p_t\end{array}$
$=\frac{1}{t} \ln \frac{p_{\infty}}{2\left(p_{\infty}-p_t\right)}$
Hence, the correct answer is option (3).
|
Daily PDF |
Sequence and series: Geometric Progression is the scoring topic of this chapter.
Question: Three distinct numbers are selected randomly from the set $\{1,2,3, \ldots \ldots, 40\}$. If the probability, that the selected numbers are in an increasing G.P. is $\frac{m}{n} \operatorname{gcd}(m, n)=1$, then $m+n$ is equal to $\_\_\_\_$ .
Solution:
Total ways to select 3 distinct numbers from $\{1,2,\ldots,40\} = ^{40}C_{3} = 9880
$
Let the three numbers in increasing G.P. be $a, ar, ar^2$ with $r = \frac{p}{q}, \gcd(p,q)=1, p>q
$
$
\Rightarrow a = k q^2, \quad ar = k p q, \quad ar^2 = k p^2
$
All terms $\leq 40 \Rightarrow k p^2 \leq 40 \Rightarrow k \leq \left[ \frac{40}{p^2} \right]
$
Possible pairs $(p,q)$ with $p > q, \gcd(p,q)=1:
$
$
\begin{aligned}
&(2,1): \left[ \frac{40}{4} \right] = 10 \\
&(3,1): \left[ \frac{40}{9} \right] = 4 \\
&(3,2): 4 \\
&(4,1): 2 \\
&(4,3): 2 \\
&(5,1): 1 \\
&(5,2): 1 \\
&(5,3): 1 \\
&(5,4): 1 \\
&(6,1): 1 \\
&(6,5): 1
\end{aligned}
$
We have used the greatest integer function to calculate the possible pairs in terms of integers,
Sum of all $ k = 10 + 4 + 4 + 2 + 2 + 1 + 1 + 1 + 1 + 1 + 1 = 28
$
Therefore, number of favorable triplets$ = 28
$
Probability $= \frac{28}{9880} = \frac{7}{2470}
$
$
\gcd(7,2470) = 1 \quad \Rightarrow \quad m=7, \quad n=2470
$
$
\therefore m + n = 7 + 2470 = 2477
$
Hence, the answer is $2477$.
|
Daily PDF |
Kinematics: Boat River Problem is a frequently asked concept of this chapter
Question: The maximum speed of a boat in still water is $27 \mathrm{~km} / \mathrm{h}$. Now this boat is moving downstream in a river flowing at $9 \mathrm{~km} / \mathrm{h}$. A man in the boat throws a ball vertically upwards with a speed of $10 \mathrm{~m} / \mathrm{s}$. The range of the ball as observed by an observer at rest on the river bank is $\_\_\_\_$ cm.
(Take $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$ )
Solution:
The velocity of the boat in still water is $27 \mathrm{~km} / \mathrm{h}$. Since the boat is moving downstream and the river flows at $9 \mathrm{~km} / \mathrm{h}$, the actual speed of the boat relative to the bank becomes:
$
v_{\text {boat }}=27+9=36 \mathrm{~km} / \mathrm{h}
$
Convert this speed from km/h to m/s by using the conversion factor $1 \mathrm{~km} / \mathrm{h}=\frac{5}{18} \mathrm{~m} / \mathrm{s}$ :
$
v_{\text {boat }}=36 \times \frac{5}{18}=10 \mathrm{~m} / \mathrm{s}
$
This is also the horizontal velocity of the ball as seen by the observer on the bank.
Next, calculate the time the ball spends in the air. The initial vertical velocity of the ball is $10 \mathrm{~m} / \mathrm{s}$. The time to reach the maximum height $t_{\mathrm{up}}$ is given by:
$
t_{\mathrm{up}}=\frac{v_{\text {initial }}}{g}=\frac{10}{10}=1 \mathrm{~s}
$
The total time of flight $t_{\text {total }}$ is twice the time to reach the maximum height:
$
t_{\text {total }}=2 \times 1=2 \mathrm{~s}
$
The horizontal range $R$ of the ball is the horizontal velocity multiplied by the total time of flight:
$
R=v_{\text {horizontal }} \quad \times t_{\text {total }}=10 \times 2=20 \mathrm{~m}
$
Finally, convert this range into centimeters:
$
R=20 \times 100=2000 \mathrm{~cm}
$
Thus, the range of the ball as observed by an observer at rest on the bank is 2000 cm .
Hence, the answer is 2000.
|
Daily PDF |
p- Block Elements: Physical Properties of Group 13 is the scoring topic of this chapter.
Question: Consider the following elements $\mathrm{In}, \mathrm{Tl}, \mathrm{Al}, \mathrm{Pb}, \mathrm{Sn}$ and Ge .
The most stable oxidation states of elements with highest and lowest first ionisation enthalpies, respectively, are
1) +2 and +3
2) (correct) +4 and +3
3) +4 and +1
4) +1 and +4
Solution:
In, TI, Al, Pb, Sn Ge
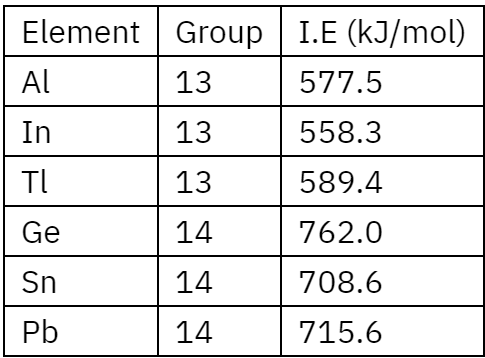
Lowest first I.E. $=\ln \Rightarrow$ most stable oxidation state $\Rightarrow+3$
Highest first I.E. $=\mathrm{Ge} \Rightarrow$ most stable oxidation state $\Rightarrow+4$
Hence, the correct answer is option (2).
|
Daily PDF |
Integral Calculus: Piecewise Definite integration is the scoring topic of this chapter.
Question: If $24 \int_0^{\frac{\pi}{4}}\left(\sin \left|4 x-\frac{\pi}{12}\right|+[2 \sin \mathrm{x}]\right) \mathrm{dx}=2 \pi+\alpha$, where [] denotes the greatest integer function, then $\alpha$ is equal to $\_\_\_\_$ .
Solution:
We split the integral at the point where the argument of the absolute value changes sign:
$
4x - \frac{\pi}{12} = 0 \implies x = \frac{\pi}{48}.
$
So,
$
\int_0^{\frac{\pi}{4}} \sin \left|4x - \frac{\pi}{12}\right| dx = \int_0^{\frac{\pi}{48}} \sin \left(\frac{\pi}{12} - 4x\right) dx + \int_{\frac{\pi}{48}}^{\frac{\pi}{4}} \sin \left(4x - \frac{\pi}{12}\right) dx.
$
Using $\sin(a - b) = \sin a \cos b - \cos a \sin b$ or simply recognizing $\sin|u| = \pm \sin u$ depending on sign,
$
= \int_0^{\frac{\pi}{48}} \sin \left(\frac{\pi}{12} - 4x \right) dx + \int_{\frac{\pi}{48}}^{\frac{\pi}{4}} \sin \left(4x - \frac{\pi}{12}\right) dx.
$
Also, evaluate the integral involving the floor function:
$
\int_0^{\frac{\pi}{4}} [2 \sin x] \, dx = \int_0^{\frac{\pi}{6}} [2 \sin x] \, dx + \int_{\frac{\pi}{6}}^{\frac{\pi}{4}} [2 \sin x] \, dx.
$
Note:
For $0 \leq x < \frac{\pi}{6}$, $2 \sin x < 1$, so $[2 \sin x] = 0$.
For $\frac{\pi}{6} \leq x \leq \frac{\pi}{4}$, $2 \sin x \geq 1$, and since $\sin x$ increases, $[2 \sin x] = 1$.
Therefore,
$
\int_0^{\frac{\pi}{6}} [2 \sin x] dx = \int_0^{\frac{\pi}{6}} 0 \, dx = 0,
$
and
$
\int_{\frac{\pi}{6}}^{\frac{\pi}{4}} [2 \sin x] dx = \int_{\frac{\pi}{6}}^{\frac{\pi}{4}} 1 \, dx = \frac{\pi}{4} - \frac{\pi}{6} = \frac{\pi}{12}.
$
Evaluate the sine integrals:
1. First integral,
$
\int_0^{\frac{\pi}{48}} \sin \left(\frac{\pi}{12} - 4x \right) dx = \int_0^{\frac{\pi}{48}} \sin \left(\frac{\pi}{12} - 4x \right) dx.
$
Let $u = \frac{\pi}{12} - 4x \Rightarrow du = -4 dx \Rightarrow dx = -\frac{du}{4}$.
Change the limits:
When $x = 0$, $u = \frac{\pi}{12}$.
When $x = \frac{\pi}{48}$, $u = 0$.
Thus,
$
\int_0^{\frac{\pi}{48}} \sin\left(\frac{\pi}{12} - 4x\right) dx = \int_{\frac{\pi}{12}}^0 \sin u \left(-\frac{1}{4}\right) du = \frac{1}{4} \int_0^{\frac{\pi}{12}} \sin u \, du = \frac{1}{4} \left(1 - \cos \frac{\pi}{12} \right).
$
2. Second integral,
$
\int_{\frac{\pi}{48}}^{\frac{\pi}{4}} \sin \left(4x - \frac{\pi}{12}\right) dx.
$
Let $v = 4x - \frac{\pi}{12} \Rightarrow dv = 4 dx \Rightarrow dx = \frac{dv}{4}$.
Change limits:
When $x = \frac{\pi}{48}$, $v = 0$.
When $x = \frac{\pi}{4}$, $v = \pi - \frac{\pi}{12} = \frac{11\pi}{12}$.
So,
$
\int_{\frac{\pi}{48}}^{\frac{\pi}{4}} \sin \left(4x - \frac{\pi}{12}\right) dx = \frac{1}{4} \int_0^{\frac{11\pi}{12}} \sin v \, dv = \frac{1}{4} \left(1 + \cos \frac{\pi}{12} \right).
$
Summing up:
$
\int_0^{\frac{\pi}{4}} \sin \left|4x - \frac{\pi}{12}\right| dx = \frac{1}{4} (1 - \cos \frac{\pi}{12}) + \frac{1}{4} (1 + \cos \frac{\pi}{12}) = \frac{1}{2}.
$
Combine everything:
$
24 \int_0^{\frac{\pi}{4}} \left(\sin |4x - \frac{\pi}{12}| + [2 \sin x] \right) dx = 24 \left( \frac{1}{2} + \frac{\pi}{12} \right) = 12 + 2 \pi.
$
Thus,
$
2\pi + \alpha = 2\pi + 12 \implies \alpha = 12.
$
Hence, the answer is 12.
|
Daily PDF |
Physics and Measurement: Dimension is the frequently asked concept of this chapter
Question: The expression given below shows the variation of velocity $(v)$ with time $(t)$,
$v=\mathrm{At}^2+\frac{\mathrm{Bt}}{\mathrm{C}+\mathrm{t}}$
The dimension of, ABC is :
1) $\left[\mathrm{M}^0 \mathrm{~L}^1 \mathrm{~T}^{-3}\right]$
2) (correct) $\left[\mathrm{M}^0 \mathrm{~L}^2 \mathrm{~T}^{-3}\right]$
3) $\left[\mathrm{M}^0 \mathrm{~L}^1 \mathrm{~T}^{-2}\right]$
4) $\left[\mathrm{M}^0 \mathrm{~L}^2 \mathrm{~T}^{-2}\right]$
Solution:
$\begin{aligned}
& {\left[\mathrm{LT}^{-1}\right]=[\mathrm{A}]\left[\mathrm{T}^2\right]=\frac{[\mathrm{B}][\mathrm{T}]}{[\mathrm{C}]+[\mathrm{T}]}} \\
& {[\mathrm{C}]=[\mathrm{T}]} \\
& {[\mathrm{A}]=\left[\mathrm{LT}^{-3}\right]} \\
& {[\mathrm{B}]=\left[\mathrm{LT}^{-1}\right]} \\
& \therefore {[\mathrm{ABC}]=\left[\mathrm{L}^2 \mathrm{~T}^{-3}\right]}
\end{aligned}$
Hence, the answer is the option (2).
|
Daily PDF |
Redox Reaction and Electrochemistry: Nernst Equation is the scoring topic of this chapter.
Question: Consider the following electrochemical cell at standard conditions.
$\begin{aligned}
& \mathrm{Au}(\mathrm{~s})\left|\mathrm{QH}_2, \mathrm{Q}\right| \mathrm{NH}_4 \mathrm{X}(0.01 \mathrm{M})| | \mathrm{Ag}^{+}(1 \mathrm{M}) \mid \mathrm{Ag}(\mathrm{~s}) \\
& \mathrm{E}_{\text {cell }}=+0.4 \mathrm{~V}
\end{aligned}$
The couple $\mathrm{QH}_2 / \mathrm{Q}$ represents quinhydrone electrode, the half cell reaction is given below
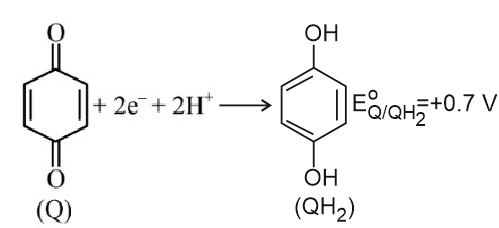
$\left[\text { Given : } \mathrm{E}_{\mathrm{Ag}^{+} / \mathrm{Ag}}^{\mathrm{o}}=+0.8 \mathrm{~V} \text { and } \frac{2.303 \mathrm{RT}}{\mathrm{~F}}=0.06 \mathrm{~V}\right]$
The $\mathrm{pK}_{\mathrm{b}}$ value of the ammonium halide salt $\left(\mathrm{NH}_4 \mathrm{X}\right)$ used here is __________. (nearest integer)
Solution:
$\begin{aligned} & \mathrm{QH}_2+2 \mathrm{Ag}^{+} \rightarrow 2 \mathrm{Ag}+\mathrm{Q}+2 \mathrm{H}^{+} \\ & \mathrm{E}=\mathrm{E}^{\circ}-\frac{0.06}{2} \log \left[\mathrm{H}^{+}\right]^2 \\ & \mathrm{E}=\mathrm{E}^{\circ}-0.06 \times \log \left[\mathrm{H}^{+}\right]\end{aligned}$
$\begin{aligned} & \mathrm{pH}=-\log \left(\mathrm{H}^{+}\right)=\frac{\mathrm{E}-\mathrm{E}^0}{0.06}=\frac{0.4-0.1}{0.06} \\ & =\frac{0.3}{0.06}=5\end{aligned}$
$\begin{aligned} & \mathrm{pH}+\left[\mathrm{NH}_4 \mathrm{X}\right]=7-\frac{1}{2} \mathrm{pK}_{\mathrm{b}}-\frac{1}{2} \log \mathrm{C} \\ & 5=7-\frac{1}{2} \times \mathrm{pK}_{\mathrm{b}}-\frac{1}{2} \log \left(10^{-2}\right) \\ & \mathrm{pK}_{\mathrm{b}}=6\end{aligned}$
Hence, the answer is 6.
|
Daily PDF |
Sets, Relations and Functions: Logarithmic Inequalities, and Reflexive, Symmetric and Transitive relationsboth are the scoring topics of this chapter.
Question: $A=\left\{x \in(0, \pi)-\left\{\frac{\pi}{2}\right\}: \log _{(2 / \pi)}|\sin x|+\log _{(2 / \pi)}|\cos x|=2\right\}$
and
$B=\{x \geq 0: \sqrt{x}(\sqrt{x}-4)-3|\sqrt{x}-2|+6=0\}$. Then $\mathrm{n}(\mathrm{A} \cup \mathrm{B})$ is equal to:
1) 4
2) 2
3) (correct) 8
4) 6
Solution:
Given sets
$
A = \left\{ x \in (0, \pi) -\left\{\frac{\pi}{2}\right\} : \log_{\frac{2}{\pi}} |\sin x| + \log_{\frac{2}{\pi}} |\cos x| = 2 \right\}
$
and
$
B = \{ x \geq 0 : \sqrt{x}(\sqrt{x} - 4) - 3|\sqrt{x} - 2| + 6 = 0 \}.
$
We need to find $ n(A \cup B) $, the number of elements in the union of sets $ A $ and $ B $.
Solution for set $ A $:
Using the logarithm property
$
\log_a b + \log_a c = \log_a (bc),
$
the equation becomes
$
\log_{\frac{2}{\pi}} (|\sin x| \cdot |\cos x|) = 2.
$
Since $ \log_a b = 2 $, it implies
$
|\sin x \cdot \cos x| = \left(\frac{2}{\pi}\right)^2 = \frac{4}{\pi^2}.
$
But as the base of the logarithm is $ \frac{2}{\pi} < 1 $, we rewrite this carefully:
The solution provided uses
$
\log_{2/\pi}(|\sin x \cos x|) = 2 \implies |\sin x \cos x| = \left(\frac{2}{\pi}\right)^2,
$
or equivalently by changing base,
$
|\sin 2x| = 2 |\sin x \cos x| = 2 \times \frac{4}{\pi^2} = \frac{8}{\pi^2}.
$
So,
$
|\sin 2x| = \frac{8}{\pi^2}.
$
Number of solutions for $ x \in (0, \pi) - \{\pi/2\} $ satisfying this equation is 4.
Solution for set $ B $:
Let
$
t = \sqrt{x}.
$
Rewrite the given equation with $ t $:
$
t(t - 4) - 3|t - 2| + 6 = 0.
$
Case 1: $ t < 2 $
$
t^2 - 4t - 3(2 - t) + 6 = 0,
$
since $ |t - 2| = 2 - t $ for $ t < 2 $.
Simplify:
$
t^2 - 4t - 6 + 3t + 6 = 0 \implies t^2 - t = 0.
$
Solve:
$
t(t - 1) = 0 \implies t = 0, 1.
$
So
$
x = t^2 = 0, 1.
$
Case 2: $ t > 2 $
$
t^2 - 4t - 3(t - 2) + 6 = 0,
$
since $ |t - 2| = t - 2 $ for $ t > 2 $.
Simplify:
$
t^2 - 4t - 3t + 6 + 6 = 0 \implies t^2 - 7t + 12 = 0.
$
Solve:
$
(t - 3)(t - 4) = 0 \implies t = 3, 4.
$
So
$
x = t^2 = 9, 16.
$
Total number of solutions:
$
n(A) = 4, \quad n(B) = 4,
$
and since the domains do not overlap,
$
n(A \cup B) = n(A) + n(B) = 8.
$
So, $ n(A \cup B) = 8 $.
Hence, the answer is Option (3)
|
Daily PDF |
Kinematics: Projectile Motion is the frequently asked concept of this chapter
Question: A ball having kinetic energy KE, is projected at an angle of $60^{\circ}$ from the horizontal. What will be the kinetic energy of ball at the highest point of its flight?
1) $\frac{(\mathrm{KE})}{8}$
2) (correct) $\frac{(\mathrm{KE})}{4}$
3) $\frac{(\mathrm{KE})}{16}$
4) $\frac{(\mathrm{KE})}{2}$
Solution:
Initial K.E,
$
\text { K.E. }=\frac{1}{2} \mathrm{mu}^2
$
Speed at the highest point
$
\begin{aligned}
\mathrm{v}&=\mathrm{u} \cos 60^{\circ}=\frac{\mathrm{u}}{2} \\
\therefore \mathrm{KE}_f &=\frac{1}{2} \mathrm{~m}\left(\frac{\mathrm{u}}{2}\right)^2 \\
& =\frac{1}{4} \times \frac{1}{2} \mathrm{mu}^2 \\
& =\frac{\mathrm{KE}}{4}
\end{aligned}
$
Hence, the answer is the option (2).
|
Daily PDF |
Redox Reaction and Electrochemistry: Molar and Equivalent Conductance is the scoring topic of this chapter.
Question: The molar conductance of an infinitely dilute solution of ammonium chloride was found to be $185 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}$ and the ionic conductance of hydroxyl and chloride ions are 170 and $70 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^1$, respectively. If molar conductance of 0.02 M solution of ammonium hydroxide is $85.5 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}$, its degree of dissociation is given by $\mathrm{x} \times 10^{-1}$. The value of $x$ is $\_\_\_\_$ (Nearest integer)
Solution:
$\begin{aligned}
& \lambda_{\mathrm{m}}^{\prime \prime} \text { of } \mathrm{NH}_4 \mathrm{Cl}=185 \\
& \left(\lambda_{\mathrm{m}}^{\circ}\right)_{\mathrm{NH}_4}+\left(\lambda_{\mathrm{m}}^{\circ}\right)_{\mathrm{Cl}^{-}}=185 \\
& \left(\lambda_{\mathrm{m}}^{\circ}\right)_{\mathrm{NH}_4}=185-70=115 \mathrm{Scm}^2 \mathrm{~mol}^{-1} \\
& \left(\lambda_{\mathrm{m}}^{\circ}\right)_{\mathrm{NH}_4 \mathrm{OH}}=\left(\lambda_{\mathrm{m}}^{\circ}\right)_{\mathrm{NH}_4^{\circ}}+\left(\lambda_{\mathrm{m}}^{\circ}\right)_{\mathrm{OH}^{-}} \\
& =115+170 \\
& \left(\lambda_{\mathrm{m}}^0\right)_{\mathrm{NH}_4 \mathrm{OH}}=285 \mathrm{Scm}^2 \mathrm{~mol}^{-1} \\
& \text { degree of dissociation }=\frac{\left(\lambda_{\mathrm{m}}\right)_{\mathrm{NH}_4 \mathrm{OH}}}{\left(\lambda_{\mathrm{m}}^{\circ}\right)_{\mathrm{NH}_4 \mathrm{OH}}} \\
& =\frac{85.5}{285} \\
& =0.3 \\
& =3 \times 10^{-1}
\end{aligned}$
Hence, the answer is 3.
|
Daily PDF |
Matrices and Determinants: Solution of System of Linear Equations Using Matrix Method is the scoring topic of this chapter.
Question: Let the system of equations
$\begin{aligned}
& x+5 y-z=1 \\
& 4 x+3 y-3 z=7 \\
& 24 x+y+\lambda z=\mu
\end{aligned}$
$\lambda, \mu \in R$, have infinitely many solutions. Then the number of the solutions of this system, If $x, y, z$ are integers and satisfy $7 \leq x+y+z \leq 77$, is
1) (correct) 3
2) 6
3) 5
4) 4
Solution:
$\begin{aligned} & \Delta=\left|\begin{array}{ccc}1 & 5 & -1 \\ 4 & 3 & -3 \\ 24 & 1 & \lambda\end{array}\right| \\ & =(3 \lambda+3)-5(4 \lambda+72)-(4-72) \\ & =-17 \lambda-289=0 \\ & \Rightarrow \lambda=-17\end{aligned}$
$\begin{aligned} & \Delta_1=\left|\begin{array}{ccc}1 & 5 & -1 \\ 7 & 3 & -3 \\ \mu & 1 & -17\end{array}\right| \\ & =(-51+3)-5(-119+3 \mu)-(7-3 \mu) \\ & =540-12 \mu \\ & \mu=\frac{540}{12}=45\end{aligned}$
$\begin{aligned} & \therefore x+5 y-z=1 \\ & 4 x+3 y-3 z=7 \\ & 24 x+y-17 z=45 \\ & z=x+5 y-1 \\ & \therefore 4 x+3 y-3 x-15 y+3=7 \\ & \Rightarrow x-12 y=4 \\ & \Rightarrow x=4+12 y \\ & \therefore z=4+12 y+5 y-1 \\ & =3+17 y \\ & \therefore(x, y, z) \equiv(4+12 k, k, 3+17 k)\ldots( \text { Assume } y=k) \\ & 7 \leq 7+30 k \leq 77 \\ & 0 \leq 30 k<70 \\ & 0 \leq k \leq 2 \cdot 3 \\ & \Rightarrow k=0,1,2 \text { (Three solutions are possible) }\end{aligned}$
Hence, the answer is option (1).
|
Daily PDF |
Day 14 focus on full Mock Test to analyse your preparation and accuracy. It helps identify strengths and weak areas for smarter improvement.
| Mock test | Mock Test 2 |
Properties of Solids and Liquids: Bernoulli's Theorem is the frequently asked question of this chapter
Question: Water flows in a horizontal pipe whose one end is closed with a valve. The reading of the pressure gauge attached to the pipe is $P_1$. The reading of the pressure gauge falls to $P_2$ when the valve is opened. The speed of water flowing in the pipe is proportional to
1) (correct) $\sqrt{\mathrm{P}_1-\mathrm{P}_2}$
2) $\left(P_1-P_2\right)^2$
3) $\left(P_1-P_2\right)^4$
4) $P_1-P_2$
Solution:
When the valve is opened, water starts flowing through the horizontal pipe, and the pressure decreases from $P_1$ to $P_2$. To determine the speed of water flow, we use Bernoulli's equation, which states:
$
P+\frac{1}{2} \rho v^2+\rho g h=\text { constant }
$
Since the pipe is horizontal, the gravitational potential energy term $\rho g h$ cancels out, reducing Bernoulli's equation to:
$
P_1+\frac{1}{2} \rho v_1^2=P_2+\frac{1}{2} \rho v_2^2
$
Assuming that the water was initially at rest $\left(v_1=0\right)$, we get:
$
P_1=P_2+\frac{1}{2} \rho v^2
$
Rearranging for $v$ :
$
v=\sqrt{\frac{2\left(P_1-P_2\right)}{\rho}}
$
Conclusion:
The speed of water flow in the pipe is proportional to the square root of the pressure difference:
$
v \propto \sqrt{P_1-P_2}
$
Hence, the answer is the option (1).
|
Daily PDF |
Solution: Elevation in Boiling Point and Depression in Freezing Point both are scoring topic of this chapter
Question: $\mathrm{CrCl}_3 \cdot \mathrm{xNH}_3$ can exist as a complex. 0.1 molal aqueous solution of this complex shows a depression in freezing point of $0.558^{\circ} \mathrm{C}$. Assuming $100 \%$ ionisation of this complex and coordination number of Cr is 6 , the complex will be (Given $\mathrm{K}_{\mathrm{f}}=1.86 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$ )
1) $\left[\mathrm{Cr}\left(\mathrm{NH}_3\right)_6\right] \mathrm{Cl}_3$
2) $\left[\mathrm{Cr}\left(\mathrm{NH}_3\right)_4 \mathrm{Cl}_2\right] \mathrm{Cl}$
3) (correct) $\left[\mathrm{Cr}\left(\mathrm{NH}_3\right)_5 \mathrm{Cl}\right] \mathrm{Cl}_2$
4) $\left[\mathrm{Cr}\left(\mathrm{NH}_3\right)_3 \mathrm{Cl}_3\right]$
Solution:
Given : $\Delta \mathrm{T}_{\mathrm{f}}=0.558^{\circ} \mathrm{C}$
$\begin{aligned}
& \mathrm{k}_{\mathrm{f}}=1.86 \frac{\mathrm{~K} \times \mathrm{kg}}{\mathrm{~mol}} \\
& 0.1 \mathrm{~m} \text { aq. sol. } \\
\Rightarrow & \Delta \mathrm{T}_{\mathrm{f}}=\mathrm{i} \times \mathrm{k}_{\mathrm{f}} \times \mathrm{m} \\
\Rightarrow & 0.558=\mathrm{i} \times 1.86 \times 0.1 \\
\Rightarrow & \mathrm{i}=3
\end{aligned}$
The van 't Hoff factor $i=3$ indicates that the complex ionizes into three particles in solution. Given the coordination number of Cr is 6 , we analyze the possible complexes:
$\begin{aligned} & {\left[\mathrm{Cr}\left(\mathrm{NH}_3\right)_5 \mathrm{Cl}\right] \mathrm{Cl}_2} \\ & {\left[\mathrm{Cr}\left(\mathrm{NH}_3\right)_4 \mathrm{Cl}_2\right] \mathrm{Cl}} \\ & {\left[\mathrm{Cr}\left(\mathrm{NH}_3\right)_6\right] \mathrm{Cl}_3} \\ & {\left[\mathrm{Cr}\left(\mathrm{NH}_3\right)_3 \mathrm{Cl}_3\right]}\end{aligned}$
The complex that gives three ions upon dissociation could be $\left[\mathrm{Cr}\left(\mathrm{NH}_3\right)_5 \mathrm{Cl}\right] \mathrm{Cl}_2$. This is because the complex will dissociate as:
$$
\left[\mathrm{Cr}\left(\mathrm{NH}_3\right)_5 \mathrm{Cl}\right]^{2+}+2 \mathrm{Cl}^{-}
$$
This results in three ions total, matching the van 't Hoff factor $i=3$.
Therefore, the complex is $\left[\mathrm{Cr}\left(\mathrm{NH}_3\right)_5 \mathrm{Cl}\right] \mathrm{Cl}_2$.
Hence, the correct answer is option (3).
|
Daily PDF |
Statistics and Probability: Dispersion (Variance and Standard Deviation) is also the scoring topic of this chapter.
Question: The variance of the numbers $8,21,34,47, \ldots, 320$, is $\_\_\_\_$ .
Solution:
Given the arithmetic sequence: $ 8, 21, 34, 47, \ldots, 320 $
First term, $ a = 8 $, common difference, $ d = 13 $
Use the $ n^{th} $ term formula:
$
a_n = a + (n-1)d
$
Put $ a_n = 320 $:
$
320 = 8 + (n-1) \times 13 \\
312 = 13(n-1) \\
n-1 = \frac{312}{13} = 24 \\
n = 25
$
Number of terms, $ n = 25 $
Mean of the AP:
$
\bar{x} = \frac{a + l}{2} = \frac{8 + 320}{2} = 164
$
Variance of AP is given by:
$
\sigma^2 = \frac{(n^2 - 1)d^2}{12}
$
Substitute values:
$
\sigma^2 = \frac{(25^2 - 1) \times 13^2}{12} = \frac{624 \times 169}{12}
$
Calculate numerator:
$
624 \times 169 = 105456
$
Divide:
$
\sigma^2 = \frac{105456}{12} = 8788
$
Hence, the answer is 8788.
|
Daily PDF |
Current Electricity: Heat and power developed in a resistor is the frequently asked question of this chapter
Question: There are $n$ identical electric bulbs, each is designed to draw a power $p$ independently from the mains supply. They are now joined in series across the mains supply. The total power drawn by the combination is
1) $p$
2) $n p$
3) (correct) $\frac{p}{n}$
4) $\frac{p}{n^2}$
Solution:
$\frac{v^2}{R}=P$
$\begin{aligned} & R_{e q}=n R \\ & P^{\prime}=\frac{v^2}{R_{e q}}=\frac{v^2}{n R} = \frac{P}{n}\end{aligned}$
Hence, the answer is option (3).
| Daily PDF | Current Electricity 10 PYQ |
Hydrocarbons: Aromaticity is a scoring topic of this chapter, and under this concept is very important for solving further problems.
Question: Designate whether each of the following compounds is aromatic or not aromatic.
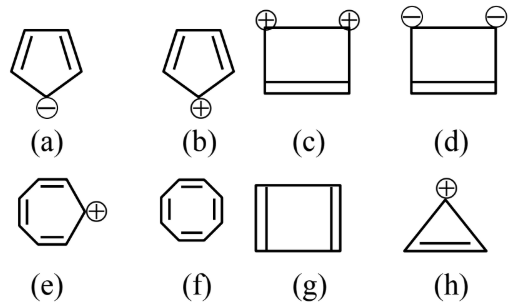
1) e, g aromatic and a, b, c, d, f, h not aromatic
2) b, e, f, g aromatic and a, c, d, h not aromatic
3) a, b, c, d aromatic and e, f, g, h not aromatic
4) a, c, d, e, h aromatic and b, f, g not aromatic
Solution:
Aromatic compounds
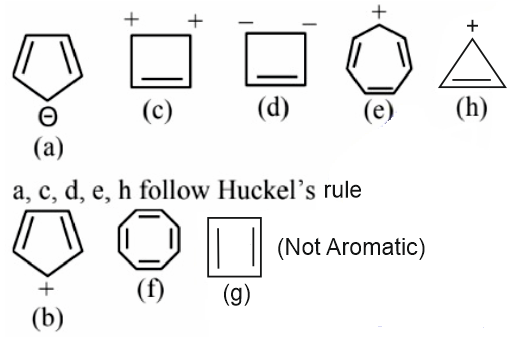
b, f, g, are not aromatic; these compounds do not follow Huckel’s rule
Hence, the correct answer is option (4).
| Daily PDF | Hydrocarbons 10 PYQ |
Complex numbers and quadratic equations: Nature of Roots is also the scoring topic of this chapter.
Question: Let the set of all values of $\mathbf{p} \in \mathbb{R}$, for which both the roots of the equation $x^2-(p+2) x+(2 p+9)=0$ are negative real numbers, be the interval $(\alpha, \beta]$. Then $\beta-2 \alpha$ is equal to
1) 0
2) 9
3) (correct) 5
4) 20
Solution:
Using the location of roots :
(i) $\mathrm{D} \geq 0$
(ii) $\frac{-\mathrm{b}}{2 \mathrm{a}}<0$
(iii) a. $\mathrm{f}(0)>0$
$\begin{aligned}
& (p+2)^2-4(2 p+9) \geq 0 \\
& (p+4)(p-8) \geq 0 \quad p+2<0 \quad 2 p+9>0
\end{aligned}$
Intersection $\mathrm{p} \in\left(-\frac{9}{2},-4\right]$
$\therefore \beta-2 \alpha=-4+9=5$
Hence, the correct answer is option (3).
Complex numbers and quadratic equations: the questions are frequently asked from Modulus of complex number and its Properties
Question: Let $z$ be a complex number such that $|z|=1$. If $\frac{2+\mathrm{k}^2 \mathrm{z}}{\mathrm{k}+\overline{\mathrm{z}}}=\mathrm{kz}, \mathrm{k} \in \mathbf{R}$, then the maximum distance of $k+i k^2$ from the circle $|z-(1+2 i)|=1$ is:
1) (correct) $\sqrt{5}+1$
2) 2
3) 3
4) $\sqrt{3}+1$
Solution:
Given: The equation,
$\frac{2+\mathrm{k}^{2} \mathrm{z}}{\mathrm{k}+\overline{\mathrm{z}}}=\mathrm{kz}$
$\Rightarrow 2+k^2z=k^2z+kz\bar{z}$
$|z|^{2} \mathrm{k}=2$-------Using the identity $z\bar{z}=|z|^2$
$\mathrm{k}=2$-----------(Using the given value of $|z|=1$)
Calculate the coordinates of the point,
$P=k+ik^2=2+i(2)^2$
$P=2+4i$
Point $\mathrm{P}(2,4)$
Similarly, calculate the circle center, by comparing,
$|z-(h+ki)|=|z-(1+2 i)|$
Centre $(h,k) =(1,2)$
Distance from the circle
$(x-1)^{2}+(y-2)^{2}=1$ is max.
if $(\mathrm{OP}+\mathrm{r})=\sqrt{1+4}+1$
$=\sqrt{5}+1$
So, the maximum distance is $\sqrt{5}+1$.
Hence, the correct answer is option (1).
Coordination Compounds: Stereoisomerism is the concept from which questions are frequently asked
Question: How many different stereoisomers are possible for the given molecule?
1) 3
2) 1
3) 2
4) 4
Solution:
R)-cis-3-hydroxy-2-butene
(S)-cis-3-hydroxy-2-butene
(R)-trans-3-hydroxy-2-butene
(S)-trans-3-hydroxy-2-butene
It has 4 stereoisomers $\left[\begin{array}{cc}\mathrm{R} \text { cis } & \mathrm{R} \text { trans } \\ \mathrm{Scis} & \mathrm{Strans}\end{array}\right]$
Hence, the correct answer is option (4).
| Daily PDF | Stereoisomerism |
Electrostatics: Dielectrics is the most asked concept of this chapter
Question: A parallel-plate capacitor of capacitance $40 \mu \mathrm{~F}$ is connected to a 100 V power supply. Now the intermediate space between the plates is filled with a dielectric material of dielectric constant $\mathrm{K}=2$. Due to the introduction of dielectric material, the extra charge and the change in the electrostatic energy in the capacitor, respectively, are -
1)
2 mC and 0.2 J
2)
8 mC and 2.0 J
3) (correct)
4 mC and 0.2 J
4)
2 mC and 0.4 J
Solution:
$\begin{aligned}
\Delta \mathrm{q} & =(\mathrm{KC}-\mathrm{C}) \mathrm{V} \\
& =40 \times 10^{-6} \times 100 \\
& =4000 \times 10^{-3}=4 \mathrm{mC}
\end{aligned}$
$\begin{aligned}
\Delta U & =\frac{1}{2} \mathrm{C}^{\prime} \mathrm{V}^2-\frac{1}{2} \mathrm{CV}^2 \\
& =\frac{1}{2} \mathrm{CV}^2(2-1) \\
& =\frac{1}{2} \times 40 \times 10^{-6} \times 10000 \\
& =0.2 \mathrm{~J}
\end{aligned}$
Hence, the answer is option (3).
| Daily PDF | Dielectrics |
Trignometry: Inverse Trigonometric Function is the most asked concept
Question: If for some $\alpha, \beta ; \alpha \leq \beta, \alpha+\beta=8$ and $\sec ^2\left(\tan ^{-1} \alpha\right)+\operatorname{cosec}^2\left(\cot ^{-1} \beta\right)=36$, then $\alpha^2+\beta$ is
Solution :
Given that for some $\alpha, \beta$ with $\alpha \leq \beta$, and
$
\alpha + \beta = 8,
$ and
$
\sec^2\left(\tan^{-1} \alpha\right) + cosec^2\left(\cot^{-1} \beta\right) = 36.
$
We need to find $\alpha^2 + \beta$.
First, use the identity for $\sec^2(\tan^{-1} x)$:
$
\sec^2(\tan^{-1} x) = 1 + \tan^2(\tan^{-1} x) = 1 + x^2.
$
Similarly, for $cosec^2(\cot^{-1} x)$:
Recall that $\cot^{-1} x = \theta \implies \cot \theta = x$.
Since $cosec^2 \theta = 1 + \cot^2 \theta$, it follows:
$
cosec^2(\cot^{-1} x) = 1 + x^2.
$
Apply these:
$
\sec^2(\tan^{-1} \alpha) + cosec^2(\cot^{-1} \beta) = (1 + \alpha^2) + (1 + \beta^2) = 2 + \alpha^2 + \beta^2 = 36.
$
Simplify:
$
\alpha^2 + \beta^2 = 34.
$
Using the given sum:
$
\alpha + \beta = 8.
$
Square both sides:
$
(\alpha + \beta)^2 = 8^2 = 64,
$
$
\alpha^2 + 2 \alpha \beta + \beta^2 = 64.
$
Substitute $\alpha^2 + \beta^2 = 34$:
$
34 + 2 \alpha \beta = 64,
$
$
2 \alpha \beta = 30,
$
$
\alpha \beta = 15.
$
Now, recall
$
\alpha + \beta = 8,
\quad \alpha \beta = 15.
$
The numbers $\alpha, \beta$ are roots of the quadratic:
$
x^2 - 8x + 15 = 0.
$
Solve for $x$:
$
x = \frac{8 \pm \sqrt{64 - 60}}{2} = \frac{8 \pm 2}{2}.
$
So,
$
x = 5 \quad \text{or} \quad 3.
$
Since $\alpha \leq \beta$, assign
$
\alpha = 3, \quad \beta = 5.
$
Finally, compute
$
\alpha^2 + \beta = 3^2 + 5 = 9 + 5 = 14.
$
Hence, the answer is 14.
| Daily PDF | Inverse Trigonometric Function |
Equilibrium: Solubility and Solubility Product is the most asked concept
Question: A solution containing 10 g of an electrolyte $\mathrm{AB}_2$ in 100 g of water boils at $100.52^{\circ} \mathrm{C}$. The degree of ionization of the electrolyte $(\alpha)$ is $\_\_\_\_$ $\times 10^{-1}$. (nearest integer)
[Given : Molar mass of $\mathrm{AB}_2=200 \mathrm{~g} \mathrm{~mol}^{-1} \cdot \mathrm{~K}_{\mathrm{b}}$ (molal boiling point elevation const. of water) $=0.52 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$, boiling point of water $=100^{\circ} \mathrm{C} ; \mathrm{AB}_2$ ionises as $\left.\mathrm{AB}_2 \rightarrow \mathrm{~A}^{2+}+2 \mathrm{~B}^{-}\right]$
Solution:
$\begin{aligned}
& \mathrm{AB}_2 \rightarrow \mathrm{~A}^{+2}+2 \mathrm{~B}^{\ominus} \\
& \mathrm{i}=1+(3-1) \alpha \\
& \mathrm{i}=1+2 \alpha \\
& \Delta \mathrm{~T}_{\mathrm{b}}=\mathrm{k}_{\mathrm{b}} \mathrm{im} \\
& 0.52=0.52(1+2 \alpha) \frac{\frac{10}{200}}{\frac{100}{1000}} \\
& 1=(1+2 \alpha) \frac{10}{20} \\
& 2=1+2 \alpha \\
& \alpha=0.5
\end{aligned}$
Ans. $\alpha=5 \times 10^{-1}$
Hence, the answer is (5).
| Daily PDF | Solubility and Solubility Product |
Optics: Young's double slit experiment is most asked concept
Question: In a Young's double slit experiment, two slits are located 1.5 mm apart. The distance of screen from slits is 2 m and the wavelength of the source is 400 nm . If the 20 maxima of the double slit pattern are contained within the central maximum of the single slit diffraction pattern, then the width of each slit is $x \times 10^{-3} \mathrm{~cm}$, where $x$-value is $\_\_\_\_$ .
Solution:
$\begin{aligned}
& d=1.5 \mathrm{~nm} \quad D=2 \mathrm{~m} \\
& \lambda=400 \mathrm{~nm} \\
& \frac{2 \lambda D}{\mathrm{a}}=20\left(\frac{\lambda \mathrm{D}}{\mathrm{~d}}\right) \\
& \left(\frac{1}{\mathrm{a}}=\frac{10}{\mathrm{~d}}\right) \Rightarrow \mathrm{a}=\frac{\mathrm{d}}{10}=\frac{1.5}{10} \mathrm{~mm} \\
& \mathrm{a}=\frac{1.5}{10} \times 10^{-3} \mathrm{~m} \\
& \mathrm{a}=15 \times 10^{-3} \times 10^{-2} \mathrm{~m} \\
& \mathrm{a}=15 \times 10^{-3} \mathrm{~cm}
\end{aligned}$
Hence, the answer is 15 .
| Daily PDF | Young's double slit experiment |
Rotational Motion: Parallel and Perpendicular Axis Theorem is the most asked concept of this chapter
Question: A rod of linear mass density ' $\lambda$ ' and length ' $L$ ' is bent to form a ring of radius ' $R$ '. The moment of inertia of ring about any of its diameter is :
1) $\frac{\lambda L^3}{16 \pi^2}$
2) $\frac{\lambda L^3}{12}$
3) $\frac{\lambda L^3}{4 \pi^2}$
4) (correct) $\frac{\lambda L^3}{8 \pi^2}$
Solution:
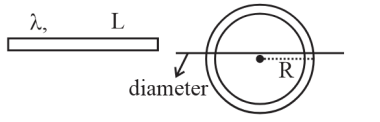
$
\begin{aligned}
& I=\frac{\mathrm{MR}^2}{2} \\
& 2 \pi \mathrm{R}=\mathrm{L} \\
& \lambda=\frac{\mathrm{M}}{\mathrm{~L}} \\
& \mathrm{I}=\frac{\lambda \mathrm{L} \times \mathrm{L}^2}{4 \pi^2 2}=\frac{\lambda \mathrm{L}^3}{8 \pi^2}
\end{aligned}
$
Hence, the answer is the option (4).
| Daily PDF | Rotational motion 10 PYQ |
Equilibrium: Le Chatelier’s principle is the concept from which question are asked almost every yesar
Question: For the reaction,
$\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})$
Attainment of equilibrium is predicted correctly by:
1)
2)
3)
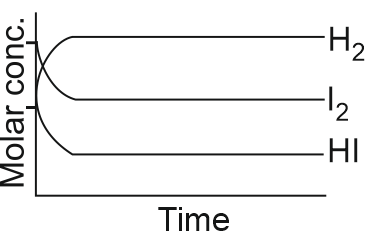
4)
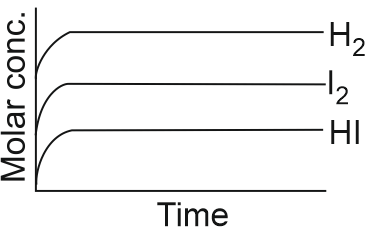
Solution:
$\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})$Concentration of $\mathrm{H}_2$ and $\mathrm{I}_2$ decreases untill equilibrium condition and concentration of HI increases till equilibrium condition and after equilibrium concentration of all the reactant and products remain constant.
Hence, the correct answer is option (2)
| Daily PDF | Equilibrium 10 PYQ |
Trigonometry: Trignometric equations is the most asked concept of this chapter
Question: The number of solutions of the equation $2 x+3 \tan x=\pi, x \in[-2 \pi, 2 \pi]-\left\{ \pm \frac{\pi}{2}, \pm \frac{3 \pi}{2}\right\}$ is
1) 6
2) 5
3) 4
4) 3
Solution:
Trigonometric Equation
The general solution of the trigonometric equation $\tan \theta=x$ is given by:
$
\theta=\tan ^{-1} x+n \pi, \quad n \in \mathbb{Z}
$
Similarly, for $\sin \theta=a$, the solutions are:
$
\theta=\sin ^{-1} a+2 n \pi \text { or } \theta=\pi-\sin ^{-1} a+2 n \pi, \quad n \in \mathbb{Z}
$
For $\cos \theta=b$, the solutions are:
$
\theta=\cos ^{-1} b+2 n \pi \text { or } \theta=-\cos ^{-1} b+2 n \pi, \quad n \in \mathbb{Z}
$
Increasing
A function $f(x)$ is said to be increasing on an interval $I$ if for any two points $x_1, x_2 \in I$ such that $x_1<x_2$, we have
$
f\left(x_1\right) \leq f\left(x_2\right)
$
If the inequality is strict, i.e.,
$
f\left(x_1\right)<f\left(x_2\right)
$
for all $x_1<x_2$ in $I$, then $f$ is strictly increasing on $I$.
Decreasing
A function $f(x)$ is said to be decreasing on an interval $I$ if for any two points $x_1, x_2 \in I$ such that $x_1<x_2$, we have
$
f\left(x_1\right) \geq f\left(x_2\right)
$
If the inequality is strict, i.e.,
$
f\left(x_1\right)>f\left(x_2\right)
$
for all $x_1<x_2$ in $I$, then $f$ is strictly decreasing on $I$.
| Daily PDF | Trigonometry 10 PYQ |
Magnetic Effects of Current and Magnetism: Motion of a charged particle in a uniform magnetic field(I) is an important concept of this chapter
Question: Question: Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: If oxygen ion $\left(\mathrm{O}^{-2}\right)$ and Hydrogen ion $\left(\mathrm{H}^{+}\right)$enter normal to the magnetic field with equal momentum, then the path of $\mathrm{O}^{-2}$ ion has a smaller curvature than that of $\mathrm{H}^{+}$.
Reason R: A proton with the same linear momentum as an electron will form a path of smaller radius of curvature on entering a uniform magnetic field perpendicularly.
In the light of the above statement, choose the correct answer from the options given below
1) (correct) A is true but R is false
2) Both A and R are true but R is NOT the correct explanation of A
3) A is false but R is true
4) Both A and R are true and R is the correct explanation of A
Solution:
Radius of curvature $R=\frac{m b}{q B}$.
$
\begin{aligned}
& r=\frac{m v}{q B} \\
& r=\frac{p}{q B}
\end{aligned}
$
since momentum is same $\Rightarrow R \propto \frac{1}{q}$.
Assertion A: since charge on $\mathrm{O}^{2-}$ is double to that of $\mathrm{H}^{+}$
⇒ Radius of curvature is smaller for $O^{2-}$.
Reason:
Since the charge is the same for a proton and an electron hence both have the same radius of curvature.
Hence, the answer is option (1).
Organic Compounds containing Oxygen: Haloform Reaction is also an important topic of this chapter
Question: The number of molecules from below that cannot give an iodoform reaction is :
Ethanol, Isopropyl alcohol, bromoacetone, 2-Butanol, 2-Butanone, Butanal, 2-Pentanone, 3-Pentanone, Pentanal and 3-Pentanol
1) 5
2) (correct) 4
3) 3
4) 2
Answer:
A compound gives a positive iodoform test if it contains either:
- A methyl ketone group $\left(\mathrm{COCH}_3\right)$
- A secondary alcohol that can be oxidised to a methyl ketone
The following will not give an iodoform reaction/test.
- Butanal- Butanal is an aldehyde; butanal does not have a $\mathrm{COCH}_3$ (methyl ketone) group.
- 3-Pentanone - This does have a $-\mathrm{COCH}_3$ group a methyl ketone in its structure.
- Pentanal - Pentanal is also an aldehyde like butanal, but does not have the $\mathrm{CH}_3-\mathrm{CO}$ - group.
- 3-Pentanol- This is a secondary alcohol, but it does not have the structure $-\mathrm{CH}(\mathrm{OH}) \mathrm{CH}_3$, which is required for oxidation to a methyl ketone.
Hence, the correct answer is option (2).
Vector Algebra: This chapter has a good weightage in the exam, and concepts like Addition and subtraction of Vectors, Vector Triple Product are frequently asked in the exam
Question: Let $\vec{a}$ and $\vec{b}$ be the vectors of the same magnitude such that $\frac{|\vec{a}+\vec{b}|+|\vec{a}-\vec{b}|}{|\vec{a}+\vec{b}|-|\vec{a}-\vec{b}|}=\sqrt{2}+1$. Then $\frac{|\vec{a}+\vec{b}|^2}{|\vec{a}|^2}$ is :
1) $2+4 \sqrt{2}$
2) $1+\sqrt{2}$
3) (correct) $2+\sqrt{2}$
4) $4+2 \sqrt{2}$
Solution:
$
\frac{|\overline{\mathrm{a}}+\overline{\mathrm{b}}|+|\overline{\mathrm{a}}-\overline{\mathrm{b}}|}{|\overline{\mathrm{a}}+\overline{\mathrm{b}}|-|\overline{\mathrm{a}}-\overline{\mathrm{b}}|}=\sqrt{2}+1
$
Apply componendo and dividendo
$
\begin{aligned}
& \Rightarrow \frac{2|\bar{a}+\bar{b}|}{2|\bar{a}-\bar{b}|}=\frac{\sqrt{2}+2}{\sqrt{2}} \\
& \Rightarrow|\bar{a}+\bar{b}|=(1+\sqrt{2})|\bar{a}-\bar{b}| \\
& \Rightarrow|\bar{a}+\bar{b}|^2=(3+2 \sqrt{2})|\bar{a}-\bar{b}|^2 \\
& \Rightarrow 2|\bar{a}|^2+2 \bar{a} \cdot \bar{b}=(3+2 \sqrt{2})\left(2|\bar{a}|^2-2 \bar{a} \cdot \bar{b}\right) \\
& \Rightarrow 2|\bar{a}|^2(2+2 \sqrt{2})=2 \bar{a} \cdot \bar{b}(4+2 \sqrt{2}) \\
& \Rightarrow \frac{\bar{a} \cdot \bar{b}}{|\bar{a}|^2}=\frac{2+2 \sqrt{2}}{4+2 \sqrt{2}}=\frac{1}{\sqrt{2}}
\end{aligned}
$
Now
$
\begin{aligned}
& \frac{|\bar{a}+\bar{b}|^2}{|\bar{a}|^2}=1+\frac{|\bar{b}|^2}{|\bar{a}|^2}+\frac{2 \bar{a} \cdot \bar{b}}{|\bar{a}|^2} \\
& =1+1+2\left(\frac{1}{\sqrt{2}}\right)=2+\sqrt{2}
\end{aligned}
$
Hence, the correct answer is option (3).
| Daily PDF | Vector Algebra 10 PYQ |
Day 7 focuses on a full Mock Test to analyse your preparation and accuracy. It helps identify strengths and weak areas for smarter improvement.
| Mock Test | Mock Test 1 |
Atoms and Nuclei: Bohr's Model of the Hydrogen Atom is the most asked concept of this chapter
Question: Assuming the validity of Bohr's atomic model for hydrogen-like ions, the radius of $\mathrm{Li}^{++}$ion in its ground state is giver $\frac{1}{X} a_0$, where $X=$ $\_\_\_\_$ .
(Where $\mathbf{a}_0$ is the first Bohr's radius.)
1) 2
2) 1
3) (correct) 3
4) 9
Solution:
The radius of a hydrogen-like ion according to Bohr's atomic model is given by the formula:
$
r=r_0 \frac{n^2}{Z}
$
Where:
$r_0$ is the first Bohr radius $\left(a_0\right)$
$n$ represents the principal quantum number
$Z$ is the atomic number of the ion
For the ion $\mathrm{Li}^{++}$, the atomic number $Z=3$ and we are considering the ground state, so $n=1$.
Plugging these values into the formula, we get:
$
r=r_0 \frac{1^2}{3}=\frac{r_0}{3}
$
This shows that the radius of $\mathrm{Li}^{++}$in its ground state is $\frac{1}{3} a_0$, meaning $X=3$.
Hence, the answer is option (3)
| Daily PDF | Atoms And Nuclei 10 PYQ |
Organic Compounds containing Oxygen: Intramolecular Aldol Condensation is the concept of this chapter, from which questions are frequently asked. This topic is very high scoring.
Question:
When 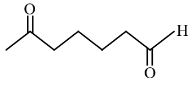
1)
2)
3)
4)
Solution:
The first step of the scheme shows aldol condensation in the presence of a base, resulting in the formation of β -hydroxy ketone with a 5-membered ring. On heating, water is eliminated and the product α , β -Unsaturated cyclopentanone is obtained.
Hence, the correct answer is option (1).
Matrices and Determinants: Properties of the Adjoint of a Matrix - Part 1 is the most asked concept of Matrices and Determinants
Question: Let I be the identity matrix of order $3 \times 3$ and for the matrix $A=\left[\begin{array}{ccc}\lambda & 2 & 3 \\ 4 & 5 & 6 \\ 7 & -1 & 2\end{array}\right],|\mathrm{A}|=-1$. Let B be the inverse of the matrix $\operatorname{adj}\left(\mathrm{A} \operatorname{adj}\left(\mathrm{A}^2\right)\right)$. Then $|(\lambda \mathrm{B}+1)|$ is equal to $\_\_\_\_$。
Solution:
Solution:
Given: the inverse of the matrix,
$
\begin{aligned}
& B=\left[\operatorname{adj}\left(A \operatorname{adj}\left(A^2\right)\right)\right]^{-1} \\
& \operatorname{Adj}\left(A^2\right)=(\operatorname{adj} A)^2 \Rightarrow A \operatorname{adj}\left(A^2\right)=A \operatorname{adj}(A) \cdot(\operatorname{adj} A) \\
& =A\left(|A| A^{-1}\right)^2=|A|^2\left(A^{-1}\right)=A^{-1} \\
& \Rightarrow B=\left(\operatorname{adj}\left(A^{-1}\right)\right)^{-1}=\left(\left|\left(A^{-1}\right)\right| A\right)^{-1}=\frac{A^{-1}}{-1}=-A^{-1} \\
& \Rightarrow B=-A^{-1}
\end{aligned}
$
Use the determinant,
$
\begin{aligned}
& |A|=-1 \\
& \left|\begin{array}{ccc}
\lambda & 2 & 3 \\
4 & 5 & 6 \\
7 & -1 & 2
\end{array}\right|=-1 \\
& \Rightarrow \lambda=3 \\
& |3 B+1|=\left|I-3 A^{-1}\right|=\frac{|A|\left|I-3 A^{-1}\right|}{|A|}=\frac{|A-3|}{|A|} \\
& =\frac{|A-3 I|}{-1}=\frac{\left|\begin{array}{ccc}
0 & 2 & 3 \\
4 & 2 & 6 \\
7 & -1 & -1
\end{array}\right|}{-1}
\end{aligned}
$
We expand along the first row:
$
\left|\begin{array}{ccc}
0 & 2 & 3 \\
4 & 2 & 6 \\
7 & -1 & -1
\end{array}\right|=0 \cdot\left|\begin{array}{cc}
2 & 6 \\
-1 & -1
\end{array}\right|-2 \cdot\left|\begin{array}{cc}
4 & 6 \\
7 & -1
\end{array}\right|+3 \cdot\left|\begin{array}{cc}
4 & 2 \\
7 & -1
\end{array}\right|
$
Now calculate the $2 \times 2$ minors:
$
\text { - }\left|\begin{array}{cc}
4 & 6 \\
7 & -1 \\
4 & 2 \\
7 & -1
\end{array}\right|=(4)(-1)-(6)(7)=-4-42=-46
$
So the determinant becomes:
$
\begin{aligned}
& -2(-46)+3(-18)=92-54=38 \\
& \Rightarrow|3 B+1|=\frac{|A-3 I|}{-1}=-38
\end{aligned}
$
Hence, the answer is -38 .
| Daily PDF | Matrices and Determinants 10 PYQ |
Oscillations and Waves: General equation of travelling is the concept of this chapter from which questions are asked every year.
Question: The equation of a wave travelling on a string is $y=\sin [20 \pi x+10 \pi t]$, where $x$ and $t$ are distance and time in SI units. The minimum distance between two points having the same oscillating speed is:
1) (correct) 5.0 cm
2) 20 cm
3) 10 cm
4) 2.5 cm
Solution:
$
\begin{aligned}
& y=\sin (20 \pi x+10 \pi t) \\
& \frac{2 \pi}{\lambda}=20 \pi \\
& \frac{\lambda}{2}=\frac{1}{20} m
\end{aligned}
$
Minimum distance between two points having same speed is $\frac{\lambda}{2}$ i.e $\frac{1}{20} \times 100 \mathrm{~cm}=5 \mathrm{~cm}$
Hence, the answer is the option (1).
| Daily PDF | Oscillations and Waves 10 PYQ |
Solutions: Concentration Terms is the most frequently asked concept of this chapter every year
Question: Assume a living cell with $0.9 \%(\omega / \omega)$ of glucose solution (aqueous). This cell is immersed in another solution having equal mole fraction of glucose and water.
(Consider the data upto first decimal place only)
The cell will :
(1) shrink since soluton is $0.5 \%(\omega / \omega)$
2) shrink since solution is $0.45 \%(\omega / \omega)$ as a result of association of glucose molecules (due to hydrogen bonding)
3) swell up since solution is $1 \%(\omega / \omega)$
4) (correct) Show no change in volume since solution is $0.9 \%(\omega / \omega)$
Solution:
Living cell has 0.9 g glucose in 100 g solution.
Which is dipped in a solution with $\mathrm{X}_{\mathrm{H}_2 \mathrm{O}}=\frac{1}{2}$.
Molecular mass of Glucose = 180
Molecular mass of water $=18$
Weight of solution $=\frac{1}{2} \times 180+\frac{1}{2} \times 18=99 \mathrm{~g}$.
So, the solution has 90 g glucose in 99 g solution or $\% w / w=90.9 \%$
Concentrated solution=Cell will shrink.
| Daily PDF | Solutions 10 PYQ |
Sets, Relations and Functions: Reflexive: Symmetric and Transitive relation is most repeated topic of this chapter
Question: Let $\mathrm{A}=\{1,2,3,4,5\}$. Let R be a relation on A defined by $x R y$ if and only if $4 x \leq 5 y$. Let $m$ be the number of elements in $R$ and $\mathbf{n}$ be the minimum number of elements from $\mathbf{A} \times \mathbf{A}$ that are required to be added to $R$ to make it a symmetric relation. Then $\mathrm{m}+\mathrm{n}$ is equal to:
1) 24
2) 23
3) (correct) 25
4) 26
Solutions:
Given : $4 x \leq 5 y$
then
$
\begin{array}{r}
\mathrm{R}=\{(1,1),(1,2),(1,3),(1,4),(1,5),(2,2),(2,3),(2,4) \\
(2,5),(3,3),(3,4),(3,5),(4,4),(4,5),(5,4),(5,5)\}
\end{array}
$
i.e. 16 elements.
i.e. $\mathrm{m}=16$
Now to make $R$ a symmetric relation add
$
\{(2,1)(3,2)(4,3)(3,1)(4,2)(5,3)(4,1)(5,2)(5,1)\}
$
i.e. $\mathrm{n}=9$
So $\mathrm{m}+\mathrm{n}=25$
Hence, the answer is the option (3).
| Daily PDF | Sets, Relations and Functions |
Properties of Solids and Liquids: Archimedes principle is the most asked concept of this chapter
Question: A wooden block floating in a bucket of water has $4 / 5$ of its volume submerged. When a certain amount of oil is poured into the bucket, it is found that the block is just under the oil surface with half of its volume under water and half in oil. The density of oil relative to that of water is :
1) 0.5
2) 0.8
3) (Correct) 0.6
4) 0.7
Solution:
$
\begin{aligned}
& P_{\text {block }}=\frac{4}{5} p_w \Rightarrow \frac{4}{5} V P_w g=m g------(1) \\
& \Rightarrow \frac{V}{2} P_w g+\frac{V}{2} p^{\prime} g=m g=\frac{4}{5} V P_w g \\
& \Rightarrow \frac{1}{2} P_w+\frac{p^{\prime}}{2}=\frac{4}{5} P_w \\
& \Rightarrow \frac{p^{\prime}}{2}=\left[\frac{4}{5}-\frac{1}{2}\right] P_w p^{\prime}=\frac{6}{10} P_w \Rightarrow P^{\prime}=\frac{3}{5} P_w=0.6 P_w
\end{aligned}
$
Hence, the answer is the option (3).
Hydrocarbons: Halogenation of Alkenes is the most frequently asked concept of thios chapter and some question of this concept are given below
Question:
Consider the above chemical reaction. The total number of stereoisomers possible for Product 'P' is __________ .
Solution:
As we have learnt,
Cis-alkene undergoes anti-addition to form a racemic mixture.

Hence, the answer is (2).
| Daily PDF | Hydrocarbons 10 PYQ |
Limit, continuity, and differentiability: Limit is also an important concept of this chapter. Questions are also frequently asked about this concept
Question: $\lim _{x \rightarrow 0}\left(\left(\frac{\left(1-\cos ^2(3 x)\right.}{\cos ^3(4 x)}\right)\left(\frac{\sin ^3(4 x)}{\left(\log _c(2 x+1)^5\right.}\right)\right)$ is equal to $\_\_\_\_$ :
1) 24
2) 9
3 ) (correct) 18
4) 15
Solution:
$
\begin{aligned}
& \lim _{x \rightarrow 0}\left[\frac{1-\cos ^2 3 x}{9 x^2}\right] \frac{9 x^2}{\cos ^3 4 x} \cdot \frac{\left(\frac{\sin 4 x}{4 x}\right)^3 \times 64 x^3}{\left[\frac{\ln (1+2 x)}{2 x}\right]^5 \times 32 x^5} \\
& \lim _{x \rightarrow 0} 2\left(\frac{1}{2} \times \frac{9}{1} \times \frac{1 \times 64}{1 \times 32}\right)=18
\end{aligned}
$
Hence, the answer is option (3).
Rotational Motion: Parallel and Perpendicular Axis Theorem is the most asked topic of this chapter
Question: The moment of inertia of a rod of mass ' M ' and length ' L ' about an axis passing through its center and normal to its length is ' $\alpha$ '. Now the rod is cut into two equal parts and these parts are joined symmetrically to form a cross shape. The moment of inertia of a cross about an axis passing through its center and normal to the plane containing the cross is :
1) $\alpha$
2) (correct) $\alpha / 4$
3) $\alpha / 8$
4) $\alpha / 2$
Solution:
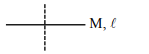
$\alpha=\frac{\mathrm{M} \ell^2}{12}$
$\begin{aligned} & \alpha^{\prime}=2\left[\frac{\frac{\mathrm{M}}{2}\left(\frac{\ell}{2}\right)^2}{12}\right] \\ & \alpha^{\prime}=\frac{\mathrm{M} \ell^2}{48}=\frac{\alpha}{4}\end{aligned}$
Hence, the answer is option (2).
| Daily PDF | Rotational Motion 10 PYQ |
Some basic concepts in chemistry: MOLE CONCEPT AND MOLAR MASS is the frequently asked topic of this chapter its pyq are given in the daily pdf
Question: What amount of bromine will be required to convert 2 g of phenol into 2 , 4 , 6 -tribromophenol? (Given molar mass in gmol − 1 of C , H , O , Br are 12 , 1 , 16 , 80 respectively)
1) (correct) 10.22 g
2) 6.0 g
3) 4.0 g
4) 20.44 g
Solution:
Moles of phenol = 2 94 = 0.021
∴ Moles of bromine = 0.021 × 3 = 0.064
∴ Mass of bromine = 0.064 × 160 = 10.22 g
Hence, the correct answer is option (1).
Limit, continuity, and differentiability: Maxima and Minima of a Function is the most frequently repeated concept of this chapter
Question: The radius of the smallest circle which touches the parabolas $y=x^2+2$ and $x=y^2+2$ is
1) $\frac{7 \sqrt{2}}{2}$
2) $\frac{7 \sqrt{2}}{16}$
3) $\frac{7 \sqrt{2}}{4}$
4) (correct) $\frac{7 \sqrt{2}}{8}$
Solution:
The given parabolas are symmetric about the line y = x .
Tangents at points $A \& B$ must be parallel to $y=x$ line, so slope of the tangents $=1$
$
\left(\frac{d y}{d x}\right)_{\min A}=1=\left(\frac{d y}{d x}\right)_{\min B}
$
For point $\mathrm{B}, \mathrm{y}=\mathrm{x}^2+2$
$
\begin{aligned}
& \qquad \frac{\mathrm{dy}}{\mathrm{dx}}=2 \mathrm{x}=1 \\
& \mathrm{x}=\frac{1}{2} \Rightarrow \mathrm{y}=\frac{9}{4} \\
& \therefore \text { Point } \mathrm{B}=\left(\frac{1}{2}, \frac{9}{4}\right) \Rightarrow \text { Point } \mathrm{A}=\left(\frac{9}{4}, \frac{1}{2}\right) \\
& \mathrm{AB}=\sqrt{\left(\frac{1}{2}-\frac{9}{4}\right)^2+\left(\frac{9}{4}-\frac{1}{2}\right)^2} \\
& =\sqrt{\frac{98}{16}}=\frac{7 \sqrt{2}}{4} \\
& \text { Radius }=\frac{7 \sqrt{2}}{8} \text { units }
\end{aligned}
$
Hence, the answer is option (4).
Electrostatics: The Parallel plate capacitor is the most asked concept of this chapter
Question: Consider a parallel plate capacitor of area A (of each plate) and separation ' d ' between the plates. If $E$ is the electric field and $\varepsilon_0$ is the permittivity of free space between the plates, then the potential energy stored in the capacitor is:-
1) (correct) $\frac{1}{2} \varepsilon_0 \mathrm{E}^2 \mathrm{Ad}$
2) $\frac{3}{4} \varepsilon_0 \mathrm{E}^2 \mathrm{Ad}$
3) $\frac{1}{4} \varepsilon_0 \mathrm{E}^2 \mathrm{Ad}$
4) $\varepsilon_0 \mathrm{E}^2 \mathrm{Ad}$
Solution:
The energy density per unit volume is given as,
$
\begin{aligned}
\frac{\mathrm{U}}{\mathrm{~V}} & =\frac{1}{2} \epsilon_0 \mathrm{E}^2 \\
\Rightarrow \mathrm{U} & =\frac{1}{2} \epsilon_0 \mathrm{E}^2 \mathrm{~V} \\
\Rightarrow \mathrm{U} & =\frac{1}{2} \epsilon_0 \mathrm{E}^2(\mathrm{Ad})
\end{aligned}
$
Hence, the answer is option (1).
| Daily PDF | Electrostatics 10 PYQ |
Chemical Thermodynamics: Gibbs Energy and Change in Gibbs Energy is the most asked concept of this chapter
Question: Match List-I with List-II.
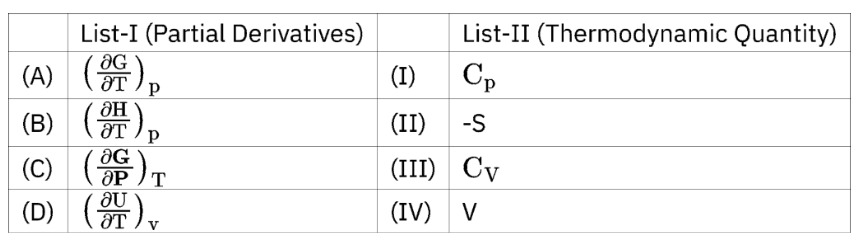
Choose the correct answer from the options given below :
1) (A)-(II), (B)-(I), (C)-(III), (D)-(IV)
2) (correct) (A)-(II), (B)-(I), (C)-(IV), (D)-(III)
3) (A)-(I), (B)-(II), (C)-(IV), (D)-(III)
4) (A)-(II), (B)-(III), (C)-(I), (D)-(IV)
Solution:
(A) $\mathrm{dG}=\mathrm{VdP}-\mathrm{SdT}$
Constant pressure
$
\begin{aligned}
& \mathrm{dG}=-\mathrm{SdT} \\
& \left(\frac{\partial \mathrm{G}}{\partial \mathrm{~T}}\right)_{\mathrm{p}}=-\mathrm{S}
\end{aligned}
$
(B) $\mathrm{dH}=(\mathrm{dq})_{\mathrm{p}}=\mathrm{nCpdT}$
$
\left(\frac{\partial \mathrm{H}}{\partial \mathrm{~T}}\right)_{\mathrm{p}}=\mathrm{C}_{\mathrm{p}}
$
(C) $\mathrm{dG}=\mathrm{VdP}-\mathrm{SdT}$
At constant temperature
$
\begin{aligned}
& \mathrm{dG}=\mathrm{VdP} \\
& \left(\frac{\partial \mathrm{G}}{\partial \mathrm{P}}\right)_{\mathrm{T}}=\mathrm{V}
\end{aligned}
$
(D) $\mathrm{dU}=\mathrm{nC}_{\mathrm{V}} \mathrm{dT}=(\mathrm{q})_{\mathrm{v}}$
$
\left(\frac{\partial \mathrm{U}}{\partial \mathrm{~T}}\right)_{\mathrm{v}}=\mathrm{C}_{\mathrm{v}}
$
Hence, the correct answer is option (2).
| Daily PDF | Chemical Thermodynamics 10 PYQ |
Integral Calculus: Area Bounded by Two Curves is the most scoring topic of this chapter
Question:Question: If the area of the region $\left\{(x, y):-1 \leq x \leq 1,0 \leq y \leq a+e^{|x|}-e^{-x}, a>0\right\}$ is $\frac{\mathrm{e}^2+8 \mathrm{e}+1}{\mathrm{e}}$, then the value of a is:
1) 7
2) 6
3) 8
4) 5
Solution:
The required area is calculated by using a definite integral,
$
\begin{aligned}
& a+\int_0^1\left(a+e^x-e^{-x}\right) d x \\
& =a+\left[a+e^x+e^{-x}\right]_0^1 \\
& 2 a+e-1+e^{-1}-1=e+8+\frac{1}{e} \\
& 2 a=10 \\
& \Rightarrow a=5
\end{aligned}
$
Hence, the correct answer is option (4).
| Daily PDF | Integral Calculus 10 PYQ |
Optics: Lens Maker’s Formula is a high-scoring topic of this Chapter
Question: A lens having a refractive index 1.6 has a focal length of 12 cm , when it is in air. Find the focal length of the lens when it is placed in water.
(Take the refractive index of water as 1.28 )
1) 355 mm
2) (correct) 288 mm
3) 555 mm
4) 655 mm
Solution:
As we know,
$
\frac{1}{\mathrm{f}}=\left[\frac{\mu_{\mathrm{L}}}{\mu_{\mathrm{m}}}-1\right]\left[\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right]
$
For air $\mu_{\mathrm{m}}=1$
$
\begin{aligned}
& \frac{1}{12}=[1.6-1]\left[\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right] \\
& \frac{1}{12}=\frac{6}{10}\left[\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right] \\
& {\left[\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right]=\frac{10}{72}}
\end{aligned}
$
For water
$
\begin{aligned}
& \frac{1}{f}=\left[\frac{1.6}{1.28}-1\right]\left[\frac{10}{72}\right]=\frac{32}{128} \times \frac{10}{72} \\
& \frac{1}{f}=\frac{1}{4} \times \frac{10}{72} \\
& f=28.8 \mathrm{~cm} \\
& f=288 \mathrm{~mm}
\end{aligned}
$
Hence answer is option (2).
| Daily PDF | Optics 10 PYQ |
Co-ordination Compounds: Crystal Field Splitting in an Octahedral Field is the most asked topic of this question
Question: Identify the homoleptic complex(es) that is/are low spin.
(A) $\left[\mathrm{Fe}(\mathrm{CN})_5 \mathrm{NO}\right]^{2-}$
(B) $\left[\mathrm{CoF}_6\right]^{3-}$
(C) $\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{4-}$
(D) $\left[\mathrm{Co}\left(\mathrm{NH}_3\right)_6\right]^{3+}$
(E) $\left[\mathrm{Cr}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right]^{2+}$
Choose the correct answer from the options given below :
1. (B) and (E) only
2. (A) and (C) only
3. (C) and (D) only
4. (C) only
Solution:
(A) $\left[\mathrm{Fe}(\mathrm{CN})_5 \mathrm{NO}\right]^{-2} \rightarrow$ Heteroleptic, $\mathrm{Fe}^{+2}, 3 \mathrm{~d}^6, \mathrm{t}_2{ }^6 \mathrm{e}_{\mathrm{g}}{ }^0, \mathrm{~d}^2 \mathrm{sp}^3$, Low spin (3d series + SFL)
(B) $\left[\mathrm{CoF}_6\right]^{-3} \rightarrow$ Homoleptic, $\mathrm{sp}^3 \mathrm{~d}^2$, High spin, $\mathrm{Co}^{+3}, 3 \mathrm{~d}^6(3 \mathrm{~d}$ series + WFL $)$
(C) $\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{-4} \rightarrow$ Homoleptic
$\mathrm{Fe}^{-2}, 3 \mathrm{~d}^6, \mathrm{~d}^2 \mathrm{sp}^3, \mathrm{t}_{2 \mathrm{~g}}{ }^6 \mathrm{eg}^0$ Low spin
( 3 d series +SFL)
(D) $\left[\mathrm{Co}\left(\mathrm{NH}_3\right)_6\right]^{+3} \rightarrow$ Homoleptic, $\mathrm{Co}^{+3} 3 \mathrm{~d}^6, \mathrm{~d}^2 \mathrm{sp}^3$.
$\mathrm{t}_{2 \mathrm{~g}}{ }^6 \mathrm{eg}^0$, Low spin (3d series + SFL)
(E) $\left[\mathrm{Cr}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right]^{+2} \rightarrow$ Homoleptic
$\mathrm{Cr}^{+2} 3 \mathrm{~d}^4, \mathrm{~d}^2 \mathrm{sp}^3$, High spin $\mathrm{t}_{2 \mathrm{~g}}{ }^3 \mathrm{e}_{\mathrm{g}}{ }^1$
Hence, the correct answer is option (3).
| Daily PDF | Coordination compound 10 PYQ |
Coordinate geometry: Centroid is the most scoring topic of this chapter
Question: Let the triangle $P Q R$ be the image of the triangle with vertices $(1,3),(3,1)$ and $(2,4)$ in the line $x+2 y=2$. If the centroid of $\triangle P Q R$ is the point $(\alpha, \beta)$, then $15(\alpha-\beta)$ is equal to :
1) 24
2) 19
3) 21
4) 22
Solution:
Let ' $G$ ' be the centroid of $\Delta$ formed by $(1,3)(3,1) \&(2,4)$.
$
G=\left(\frac{1+3+2}{3}, \frac{3+1+4}{3}\right)=\left(2, \frac{8}{3}\right) .
$
Reflection of the centroid $G$ about the line $x+2 y-2=0$.
The formula for reflection of a point ( $x_0, y_0$ ) about the line $A x+B y+C=0$ is:
$
\frac{\alpha-x_0}{A}=\frac{\beta-y_0}{B}=-\frac{2\left(A x_0+B y_0+C\right)}{A^2+B^2}
$
Here, $A=1, B=2, C=-2$.
$
\frac{\alpha-2}{1}=\frac{\beta-\frac{8}{3}}{2}=-2 \frac{\left(2+\frac{16}{3}-2\right)}{1+4}=\frac{-2}{5}\left(\frac{16}{3}\right)=-\frac{32}{15}
$
Then,
$
\begin{aligned}
& \alpha=2+1 \times\left(-\frac{32}{15}\right)=2-\frac{32}{15}=\frac{30-32}{15}=-\frac{2}{15}, \\
& \beta=\frac{8}{3}+2 \times\left(-\frac{32}{15}\right)=\frac{8}{3}-\frac{64}{15}=\frac{40}{15}-\frac{64}{15}=-\frac{24}{15}=-\frac{8}{5}
\end{aligned}
$
So, $\alpha-\beta=-\frac{2}{15}-\left(-\frac{8}{5}\right)=-\frac{2}{15}+\frac{24}{15}=\frac{22}{15}$
$
\therefore 15(\alpha-\beta)=15 \times \frac{22}{15}=22
$
Hence, the correct answer is option (4).
| Daily PDF | Coordination Geometry 10 PYQ |
The JEE Mains 2026 Booster Series has been specifically designed for fast-track preparation during the most crucial last-minute phase. The focus on JEE main high-weightage topics along with a strong element of concept reinforcement and quick revision, contributes significantly to the entire preparation process. In tandem with this, the Percentile Booster Series together helps in enhancing the accuracy of students through daily practice and mock tests so that they can score well on the actual exam. The Rank Booster Test Series has full-length and chapter-wise tests valid for the JEE 2026. Tests are based on the latest pattern of the JEE exam and will serve as a further distinguishing feature to sharpen the competitive edge. Students will track progress through the JEE Booster 2026 Checklist that will ensure students cover every important topic, formula, and test before the main examination.
Frequently Asked Questions (FAQs)
Your percentile will be boosted through four primary means:
Strategic Focus: prioritise high-weightage chapters and most scoring topics.
Speed and Accuracy: Daily practices and mini-mock tests enhance question-solving speed and minimise careless mistakes.
Error Analysis: Proper analysis of the mock tests and highlights the repeating mistakes (conceptual errors vs. calculation errors vs. speed issues), thus allowing specific corrective measures to be undertaken.
This article provides you with a structured Strategy of 30 day for your jee mains preparation.
It is a 30-day structured revision with the goal of maximising effectiveness and significantly raising the candidate's score for the JEE Mains 2026 examination. This plan solely focuses on high-yield and high-weightage topics important for rank enhancement, thereby ensuring that whatever time has been invested by the candidate, he/she receive triple rewards.
On Question asked by student community
decent chances actually as home state quota seats are 50%. allotments will depend on the JEE rank and not percentile though. in 2025, for female supernumerary it closed at 9286 rank while for open gen it closed at 5573.
So, would advise to use this tool to check the probable
yes you will. Ususally the return is within 7 days i it has failed at the gateway level which it seems to be. Please wait. You will get the money back
Slim chances as in 2025 the closing rank was 118 for SPA Delhi for B.Arch. You will need to wait for the rank list to come in April before getting a better picture. Please check https://engineering.careers360.com/jee-main-college-predictor for the predictions.
Check out https://engineering.careers360.com/jee-main-rank-predictor to know the probable rank
Hi Smita Sharma,
With 47 percentile in JEE Mains 2026, you might get rank around 7,00,000 plus which is very high. Check the link below for the Best engineering colleges available for you based on yours percentile.
Link 1: https://engineering.careers360.com/colleges/list-of-engineering-colleges-in-pune-accepting-jee-main
Hey Abhinav!
You can start your JEE Preparation with ICSE. You can check How to Prepare for JEE Main 2026?- Study Plan and start you preparation.
Among top 100 Universities Globally in the Times Higher Education (THE) Interdisciplinary Science Rankings 2026
Recognized as Institute of Eminence by Govt. of India | NAAC ‘A++’ Grade | Upto 75% Scholarships
70th University Ranked by NIRF | 80th Engineering Rank by NIRF | Accredited by NBA and NAAC A+
Last Date to Apply: 28th Feb | Ranked #43 among Engineering colleges in India by NIRF | Highest Package 1.3 CR , 100% Placements
Highest CTC 44.14 LPA | UGC Approved | 1600+ Recruiters | 100% Placement
NAAC A++ Grade | Recognized as Category-1 Deemed to be University by UGC | 41,000 + Alumni Imprints Globally