Top 25 Repeated JEE Mains Questions to Score 90+ in Physics
Getting above 90 in Physics through JEE Main is not about solving thousands of problems, but mastering the right questions. Analyzing JEE Main Physics PYQs for the last 15 years gives away a repeated and narrow set of choices of concepts and the pattern of questions. This article will bring out the Top 25 Repeated JEE Mains Questions to Score 90+ in Physics over the years. Solving these repeated questions of JEE Main Physics can help aspirants highly improve in accuracy, speed, and confidence to achieve that mark without much stress.
Also Check: JEE Main Last Minute Preparation Tips

High-Scoring Chapters of JEE Main Physics to Score 90+
JEE Main Physics can be done really well if you keep studying such chapters that have consistently carried high weightage in past years and repeated PYQ patterns, and you can score above 90. The table below shows the most scoring Physics chapters for Physics PYQs to score 90+ in JEE Main, expected question frequency, and scoring potential.
|
Chapter Name |
Percentage Distribution |
|
Optics |
7.54% |
|
Properties of Solids and Liquids |
7.01% |
|
Electrostatics |
7.41% |
|
Current Electricity |
6.85% |
|
Electromagnetic Induction and Alternating Currents |
6.23% |
| Magnetic Effects of Current and Magnetism | 5.86% |
Physics Top Highest Repeated Concepts of the Last Five Years
|
Concept Name |
Total Number of Questions from last five years |
|
De-broglie wavelength of an electron |
38 |
|
Logic Gates |
36 |
|
Parallel Grouping of Resistance |
33 |
|
Projectile Motion |
33 |
|
Nature of Electromagnetic Waves |
31 |
| Hooke’s law | 29 |
Top 25 Repeated JEE Mains Questions in Physics
The questions are based on highly repeated concepts in the previous few years, concepts that appear almost every year in JEE Main Physics with maximum scoring potential if prepared well.
Question 1: A particle is projected at an angle of $30^{\circ}$ from horizontal at a speed of $60 \mathrm{~m} / \mathrm{s}$. The height traversed by the particle in the first second is $h_0$ and height traversed in the last second, before it reaches the maximum height, is $h_1$. Then $h_0: h_1$ is________.
$\left[\right.$ Take, $\left.g=10 \mathrm{~m} / \mathrm{s}^2\right]$
Solution:
Given Data:
Initial velocity: $u=60 \mathrm{~m} / \mathrm{s}$
Angle of projection: $\theta=30^{\circ}$
Acceleration due to gravity: $g=10 \mathrm{~m} / \mathrm{s}^2$
We need to find the ratio of:
Height traversed in the first second $\left(h_0\right)$
Height traversed in the last second before reaching maximum height $\left(h_1\right)$
Step 1: Find the Vertical Component of Velocity
The initial vertical velocity:
$
u_y=u \sin 30^{\circ}=60 \times \frac{1}{2}=30 \mathrm{~m} / \mathrm{s}
$
Step 2: Find the Time to Reach Maximum Height
At the maximum height, the vertical velocity becomes zero:
$
\begin{aligned}
& v_y=u_y-g t \\
& 0=30-10 t \\
& t=\frac{30}{10}=3 \mathrm{~s}
\end{aligned}
$
So, the total time to reach maximum height is 3 seconds.
Step 3: Height Traversed in the First Second $\left(h_0\right)$
Using the equation of motion:
$
h_0=u_y t+\frac{1}{2} a_y t^2
$
For $t=1 \mathrm{~s}$ :
$
h_0=(30 \times 1)+\frac{1}{2}\left(-10 \times 1^2\right)
$
$
h_0=30-5=25 \mathrm{~m}
$
Step 4: Height Traversed in the Last Second $\left(h_1\right)$
The height traversed in the last second before reaching maximum height is given by:
$
h_1=v_y t-\frac{1}{2} a_y t^2
$
$
\mathrm{h}_1=0-\frac{1}{2}\left(-10 \times 1^2\right)=5 \mathrm{~m}
$
Step 5: Find the Ratio $h_0: h_1$
$
h_0: h_1=25: 5=5: 1
$
Hence, the answer is 5.
Question 2: The angle of projection for a projectile to have same horizontal range and maximum height is :
1) $\tan ^{-1}(2)$
2) (correct) $\tan ^{-1}(4)$
3) $\tan ^{-1}\left(\frac{1}{4}\right)$
4) $\tan ^{-1}\left(\frac{1}{2}\right)$
Solution:
$\mathrm{\begin{aligned} & \frac{u^2 \sin 2 \theta}{g}=\frac{u^2 \sin ^2 \theta}{2 g} \\ & 4 \sin \theta \cos \theta=\sin ^2 \theta \\ & 4=\tan \theta\end{aligned}}$
$\theta=\tan ^{-1}(4)$
Hence, the answer is the option (2).
Question 3: The maximum height reached by a projectile is 64 m. If the initial velocity is halved, the new maximum height of the projectile is ______ m.
Solution:
$ \mathrm{H}_{\max }=\frac{\mathrm{u}^2 \sin ^2 \theta}{2 \mathrm{~g}} \\ $
$ \frac{\mathrm{H}_{1 \max }}{\mathrm{H}_{2 \max }}=\frac{\mathrm{u}_1^2}{\mathrm{u}_2^2} $
$\frac{64}{\mathrm{H}_{2 \max }}=\frac{\mathrm{u}^2}{(\mathrm{u} / 2)^2} $
$ \mathrm{H}_{2 \max }=16 \mathrm{~m}$
Hence the answer is 16.
Question 4: The initial speed of a projectile fired from ground is $u$ At the highest point during its motion, the speed of projectile is $\frac{\sqrt{3}}{2} u$. The time o flight of the projectile is :
1) $\frac{2 \mathrm{u}}{\mathrm{g}}$
2) $\frac{\mathrm{u}}{2 \mathrm{~g}}$
3) $\frac{\sqrt{3} u}{g}$
4) (correct) u
Solution :
At the highest point -
$\begin{aligned}
& \mathrm{u} \cos \theta=\frac{\sqrt{3} \mathrm{u}}{2} \\
& \theta=30 \\
& \mathrm{~T}=\frac{2 \mathrm{u} \sin \theta}{\mathrm{~g}}=\frac{\mathrm{u}}{\mathrm{~g}}
\end{aligned}$
Hence, the answer is the option (4).
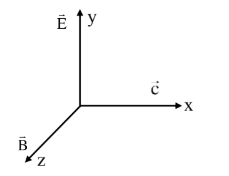
Question 5: A plane electromagnetic wave propagates along the $+x$ direction in free space. The components of the electric field, $\vec{E}$ and magnetic field, $\vec{B}$ vectors associated with the wave in Cartesian frame are:
1) $\mathrm{E}_y, \mathrm{~B}_{\mathrm{x}}$
2) (correct) $\mathrm{E}_{\mathrm{y}}, \mathrm{B}_{\mathrm{z}}$
3) $E_x, B_y$
4) $\mathrm{E}_z, \mathrm{~B}_y$
Solution:
Direction of propagation$
=\overrightarrow{\mathrm{E}} \times \overrightarrow{\mathrm{B}}
$
$E \rightarrow y, B \rightarrow z, c \rightarrow x$
$\hat{\mathrm{E}} \times \hat{\mathrm{B}}=\hat{\mathrm{j}} \times \hat{\mathrm{k}}=\hat{\mathrm{i}}=\hat{\mathrm{c}}$
Hence, the answer is the option (2).
Question 6: The magnetic field of an E.M. wave is given by
$\overrightarrow{\mathrm{B}}=\left(\frac{\sqrt{3}}{2} \hat{\mathrm{i}}+\frac{1}{2} \hat{\mathrm{j}}\right) 30 \sin \left[\omega\left(\mathrm{t}-\frac{\mathrm{z}}{\mathrm{c}}\right)\right] \text { (S.I. Units) }$
The corresponding electric field in SI units is :
1) $\overrightarrow{\mathrm{E}}=\left(\frac{1}{2} \hat{\mathrm{i}}-\frac{\sqrt{3}}{2} \hat{\mathrm{j}}\right) 30 \mathrm{c} \sin \left[\omega\left(\mathrm{t}-\frac{\mathrm{z}}{\mathrm{c}}\right)\right]$
2) $\overrightarrow{\mathrm{E}}=\left(\frac{3}{4} \hat{\mathrm{i}}+\frac{1}{4} \hat{\mathrm{j}}\right) 30 \mathrm{c} \cos \left[\omega\left(\mathrm{t}-\frac{\mathrm{z}}{\mathrm{c}}\right)\right]$
3) $\overrightarrow{\mathrm{E}}=\left(\frac{1}{2} \hat{\mathrm{i}}+\frac{\sqrt{3}}{2} \hat{\mathrm{j}}\right) 30 \mathrm{c} \sin \left[\omega\left(\mathrm{t}+\frac{\mathrm{z}}{\mathrm{c}}\right)\right]$
4) $\overrightarrow{\mathrm{E}}=\left(\frac{\sqrt{3}}{2} \hat{\mathrm{i}}-\frac{1}{2} \hat{\mathrm{j}}\right) 30 \mathrm{c} \sin \left[\omega\left(\mathrm{t}+\frac{\mathrm{z}}{\mathrm{c}}\right)\right]$
Solution:
$\begin{aligned} & \vec{B}=\left(\frac{\sqrt{3}}{2} \hat{i}+\frac{1}{2} \hat{j}\right) 30 \sin \left[\omega\left(t-\frac{z}{c}\right)\right] \\ & \vec{E}=\vec{B} \times \overrightarrow{\mathrm{c}} \text { and } E_0 = B_0 c \\ & \hat{E} = \left(\frac{\sqrt{3}}{2}(-\hat{j})+\frac{1}{2} \hat{i}\right) \\ & E_0=30 c \\ & \vec{E}=\left(\frac{1}{2} \hat{i}-\frac{\sqrt{3}}{2} \hat{j}\right) 30 c \sin \left[\omega\left(t-\frac{z}{c}\right)\right]\end{aligned}$
Hence, the answer is the option (1).
Question 7: The magnetic field in a plane electromagnetic wave is $B_y=\left(3.5 \times 10^{-7}\right) \sin \left(1.5 \times 10^3 x+0.5 \times 10^{11} \mathrm{t}\right) \mathrm{T}$. The corresponding electric field will be
1) $\mathrm{E}_{\mathrm{y}}=1.17 \sin \left(1.5 \times 10^3 \mathrm{x}+0.5 \times 10^{11} \mathrm{t}\right) \mathrm{Vm}^{-1}$
2) (correct) $\mathrm{E}_{\mathrm{z}}=105 \sin \left(1.5 \times 10^3 \mathrm{x}+0.5 \times 10^{11} \mathrm{t}\right) \mathrm{Vm}^{-1}$
3) $\mathrm{E}_{\mathrm{z}}=1.17 \sin \left(1.5 \times 10^3 \mathrm{x}+0.5 \times 10^{11} \mathrm{t}\right) \mathrm{Vm}^{-1}$
4) $\mathrm{E}_{\mathrm{y}}=10.5 \sin \left(1.5 \times 10^3 \mathrm{x}+0.5 \times 10^{11} \mathrm{t}\right) \mathrm{Vm}^{-1}$
Solution :
$\begin{aligned}
& \mathrm{E}_0=\mathrm{B}_0 \mathrm{C} \\
& \mathrm{E}_0=3 \times 10^8 \times\left(3.5 \times 10^{-7}\right) \sin \left(1.5 \times 10^3 \mathrm{x}+0.5 \times 10^{11} \mathrm{t}\right) \\
& \mathrm{E}_0=105 \sin \left(1.5 \times 10^3 \mathrm{x}+0.5 \times 10^{11} \mathrm{t}\right) \mathrm{Vm}^{-1}
\end{aligned}$
Hence, the answer is the option (2).
Question 8: A plane electromagnetic wave of frequency 20 MHz travels in free space along the $+x$ direction. At a particular point in space and time, the electric field vector of the wave is $\mathrm{E}_{\mathrm{y}}=9.3 \mathrm{Vm}^{-1}$. Then, the magnetic field vector of the wave at that point is-
1) $\mathrm{B}_{\mathrm{z}}=9.3 \times 10^{-8} \mathrm{~T} $
2) $\mathrm{B}_{\mathrm{z}}=1.55 \times 10^{-8} \mathrm{~T}$
3) $\mathrm{B}_{\mathrm{z}}=6.2 \times 10^{-8} \mathrm{~T}$
4) (correct) $\mathrm{B}_{\mathrm{z}}=3.1 \times 10^{-8} \mathrm{~T}$
Solution:
$\begin{aligned}
& \mathrm{E}=\mathrm{Bc} \\
& 9.3=\mathrm{B} \times 3 \times 10^8 \\
& \mathrm{~B}=\frac{9.3}{3 \times 10^8}=3.1 \times 10^{-8} \mathrm{~T}
\end{aligned}$
Hence, the answer is the option (4).
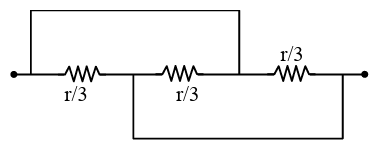
Question 9:Find the equivalent resistance between two ends of the following circuit.
1) r
2) $\frac{r}{6}$
3) (correct) $\frac{r}{9}$
4) $\frac{r}{3}$
Solution:
All are in parallel
$R_{e q}=\frac{r / 3}{3}=r / 9$
Hence, the answer is the option (3).
Question 10:
The equivalent resistance of the following network is ________ $\Omega$
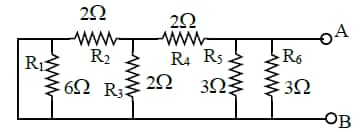
Solution:
$6 \Omega$ is short circuit
$
R_{e q}=3 \times \frac{1}{3}=1 \Omega
$
Hence, the answer is 1.
Question 11: Refer to the circuit diagram given in the figure, which of the following observation are correct?
A. The total resistance of the circuit is $6 \Omega$.
B. Current in Ammeter is 1 A
C. Potential across AB is 4 volts.
D. Potential across CD is 4 volts:
E. The total resistance of the circuit is $8 \Omega$.
Choose the correct answer from the options given below:
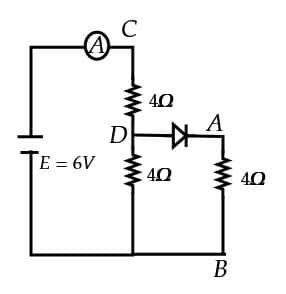
1) (correct) A, B and D only
2) A, C and D only
3) B, C and E only
4) A, B and C only
Solution:
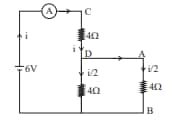
$\begin{aligned} & \text { Req }=4+\frac{4 \times 4}{4+4} \\ & =6 \Omega \\ & i=\frac{6}{6} \\ & =1 \mathrm{~A} \\ & V_{A B}=\frac{i}{2} \times R \\ & =\frac{1}{2} \times 4 \quad=2 \mathrm{~V}\end{aligned}$
$\begin{aligned} & V_{C D}=i R \\ & =1 \times 4 \\ & =4 \mathrm{~V}\end{aligned}$
Hence, the answer is option (1).
Question 12: In the given circuit 'a' is an arbitrary constant. The value of m for which the equivalent circuit resistance is minimum, will be $\sqrt{\frac{x}{2}}$. The value of $x$ is
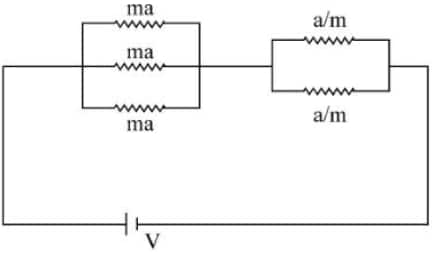
Solution:
$
\begin{aligned}
\text { Req } & =\frac{\mathrm{ma}}{3}+\frac{(\mathrm{a} / \mathrm{m})}{2} \\
& =\frac{\mathrm{ma}}{3}+\frac{\mathrm{a}}{2 \mathrm{~m}} \\
& =\frac{2 \mathrm{~m}^2 \mathrm{a}+3 \mathrm{a}}{6 \mathrm{~m}} \\
& =\frac{\mathrm{ma}}{3}+\frac{\mathrm{a}}{2 \mathrm{~m}}
\end{aligned}
$
For $\mathrm{R}_{\text {eq }}$ to be minimum,
$
\begin{aligned}
& \frac{\mathrm{dReq}}{\mathrm{dm}}=0 \\
& \frac{\mathrm{a}}{3}-\frac{\mathrm{a}}{2 \mathrm{~m}^2}=0 \\
& \frac{\mathrm{a}}{3}=\frac{\mathrm{a}}{2 \mathrm{~m}^2} \Rightarrow \mathrm{~m}^2=\frac{3}{2} \\
& \quad \mathrm{~m}=\sqrt{\frac{3}{2}}
\end{aligned}
$
Hence, the answer is option (3).
Question 13: A proton of mass ' $\mathrm{m}_{\mathrm{p}}$ ' has the same energy as that of a photon of wavelength' $\lambda$ '. If the proton is moving at a non-relativistic speed, then the ratio of its de Broglie wavelength to the wavelength of the photon is.
1) $\frac{1}{c} \sqrt{\frac{2 E}{m_p}}$
2) $\frac{1}{c} \sqrt{\frac{E}{m_p}}$
3) (correct $\frac{1}{c} \sqrt{\frac{E}{2 m_p}}$
4) $\frac{1}{2 c} \sqrt{\frac{E}{m_p}}$
Solution:
E is missing in the question but considering E as energy, the solution will be
$\begin{aligned}
& \mathrm{E}_{\text {photon }}=\frac{\mathrm{hc}}{\lambda}=\mathrm{E} ; \mathrm{E}_{\text {proton }}=\frac{1}{2} \mathrm{~m}_{\mathrm{p}} \mathrm{v}^2=\mathrm{E} \\
& \frac{\lambda_{\text {proton }}}{\lambda_{\text {photon }}}=\frac{\mathrm{h} / \mathrm{p}}{\mathrm{hc} / \mathrm{E}}=\frac{\mathrm{h} / \sqrt{2 \mathrm{~m}_{\mathrm{p}} \mathrm{E}}}{\mathrm{hc} / \mathrm{E}} \\
& =\frac{\mathrm{E}}{\mathrm{c} \sqrt{2 \mathrm{~m}_{\mathrm{p}} \mathrm{E}}} \\
& \frac{\lambda_{\text {proton }}}{\lambda_{\text {photon }}}=\frac{1}{\mathrm{c}} \sqrt{\frac{\mathrm{E}}{2 \mathrm{~m}_{\mathrm{p}}}}
\end{aligned}$
Hence, the answer is the option (3).
Question 14: A proton and an electron are associated with same de-Broglie wavelength. The ratio of their kinetic energies is : (Assume $\mathrm{h}=6.63 \times 10^{-34} \mathrm{~J} \mathrm{~s}, \mathrm{~m}_{\mathrm{e}}=9.0 \times 10^{-31} \mathrm{~kg}$ and $\mathrm{m}_{\mathrm{p}}=1836$ times $\mathrm{m}_{\mathrm{e}}$ )
1) (correct) $1: 1836$
2) $1: \frac{1}{1836}$
3) $1: \frac{1}{\sqrt{1836}}$
4) $1: \sqrt{1836}$
Solution:
$\lambda$ is same for both
$\begin{aligned}
& P=\frac{h}{\lambda} \text { same for both } \\
& P=\sqrt{2 \mathrm{mK}}
\end{aligned}$
Hence,
$\begin{aligned}
\mathrm{K} & \propto \frac{1}{\mathrm{~m}} \\
\Rightarrow & \frac{\mathrm{KE}_{\mathrm{p}}}{\mathrm{KE}_{\mathrm{e}}}=\frac{\mathrm{m}_{\mathrm{e}}}{\mathrm{~m}_{\mathrm{p}}}=\frac{1}{1836}
\end{aligned}$
Hence, the answer is option (1).
Question 15: A proton and an electron have the same de Broglie wavelength. If $K_p$ and $K_e$ be the kinetic energies of proton and electron respectively. Then choose the correct relation :
1) $\mathrm{K}_{\mathrm{p}}>\mathrm{K}_{\mathrm{e}}{ }^2$
2) $K_p=K_e$
3) $\mathrm{K}_{\mathrm{p}}=\mathrm{K}_{\mathrm{e}}{ }^2$
4) (correct) $\mathrm{K}_{\mathrm{p}}<\mathrm{K}_{\mathrm{e}}$
Solution:
De Broglie wavelength of proton \& electron $=\lambda$
$
\begin{aligned}
& \because \lambda=\frac{\mathrm{h}}{\mathrm{p}} \\
& \therefore \mathrm{p}_{\text {proton }}=\mathrm{p}_{\text {electron }} \\
& \because \mathrm{KE}=\frac{\mathrm{p}^2}{2 \mathrm{~m}} \\
& \therefore \mathrm{KE}_{\text {proton }}<\mathrm{KE}_{\text {electron }} \\
& {\left[\mathrm{K}_{\mathrm{p}}<\mathrm{K}_{\mathrm{e}}\right]}
\end{aligned}
$
Hence, the answer is option (4).
Question 16: An $\alpha$-particle, a proton and an electron have the same kinetic energy. Which one of the following is correct in the case of their de-Broglie wavelength:
1) (correct) $\lambda_\alpha<\lambda_{\mathrm{p}}<\lambda_{\mathrm{e}}$
2) $\lambda_\alpha=\lambda_{\mathrm{p}}=\lambda_{\mathrm{e}}$
3) $\lambda_\alpha>\lambda_{\mathrm{p}}>\lambda_{\mathrm{e}}$
4) $\lambda_\alpha>\lambda_{\mathrm{p}}<\lambda_{\mathrm{e}}$
Solution:
$\begin{aligned}
& \lambda=\frac{\mathrm{h}}{\sqrt{2 \mathrm{mkE}}} \alpha \frac{1}{\sqrt{\mathrm{~m}}} \\
& \mathrm{~m}_{\mathrm{a}}>\mathrm{m}_{\mathrm{p}}>\mathrm{m}_{\mathrm{e}} \\
& \therefore \lambda_{\mathrm{a}}<\lambda_{\mathrm{p}}<\lambda_{\mathrm{e}}
\end{aligned}$
Hence, the answer is the option (1).
Question 17: The output of the circuit is low (zero) for :
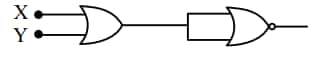
(A) $\mathrm{X}=0, \mathrm{Y}=0$ (B) $X=0, Y=1$
(C) $\mathrm{X}=1, \mathrm{Y}=0$ (D) $\mathrm{X}=1, \mathrm{Y}=1$
Choose the correct answer from the options given below :
1) (A), (C) and (D) only
2) (A), (B) and (C) only
3) (correct) (B), (C) and (D) only
4) (A), (B) and (D) only
Solution:
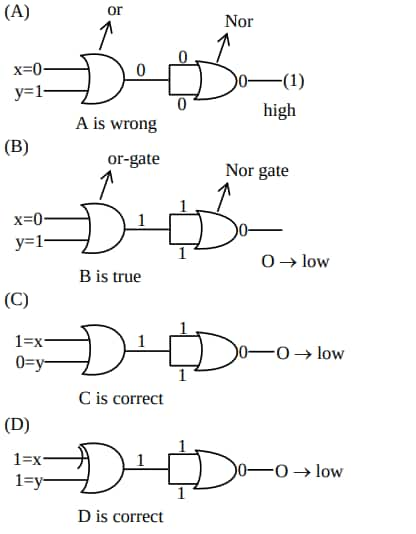
Hence, the answer is the option (3).
Question 18: The output (Y) of logic circuit given below is 0 only when :
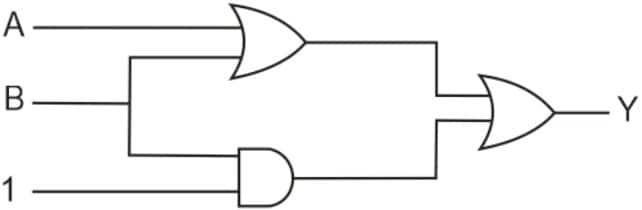
1) $A=1, B=0$
2) (correct) $A=0, B=0$
3) $A=1, B=1$
4) $A=0, B=1$
Solution:
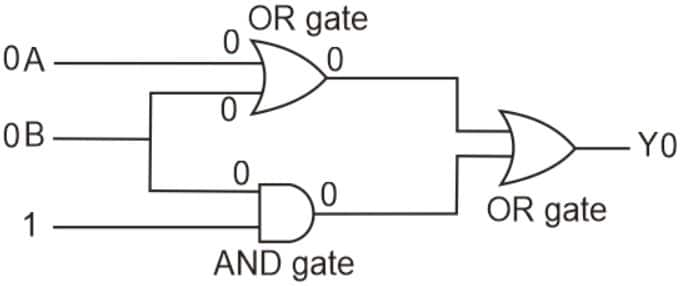
Hence, the answer is the option 2.
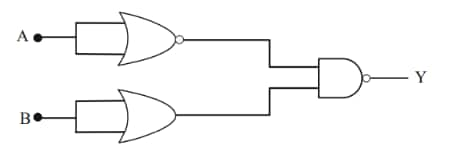
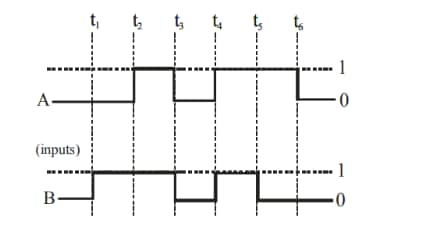
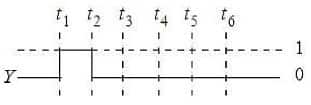
Question 19: For the following circuit and given inputs A and B, choose the correct option for output 'Y'
1)

2)

3)

4)
Solution:
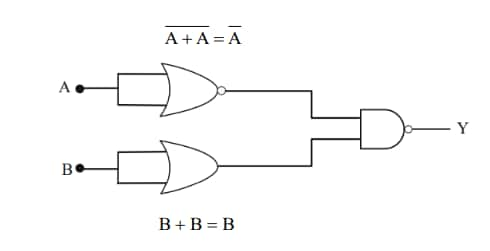
Output,
$\mathrm{y}=\overline{\overline{\mathrm{A}} \cdot \mathrm{B}}=\overline{\overline{\mathrm{A}}}+\overline{\mathrm{B}} = A + \overline{B}$
$\begin{array}{ll}
\mathrm{t}_1 \text { to } \mathrm{t}_2, & \mathrm{~A}=0, \mathrm{~B}=1, \mathrm{Y}=0 \\
\mathrm{t}_2 \text { to } \mathrm{t}_3 & \mathrm{~A}=1, \mathrm{~B}=1, \mathrm{Y}=1 \\
\mathrm{t}_3 \text { to } \mathrm{t}_4 & \mathrm{~A}=0, \mathrm{~B}=0, \mathrm{Y}=1 \\
\mathrm{t}_4 \text { to } \mathrm{t}_5, & \mathrm{~A}=1, \mathrm{~B}=1, \mathrm{Y}=1 \\
\mathrm{t}_5 \text { to } \mathrm{t}_6, & \mathrm{~A}=1, \mathrm{~B}=0, \mathrm{Y}=1 \\
\mathrm{After}~\mathrm{t}_6, & \mathrm{~A}=0, \mathrm{~B}=0, \mathrm{Y}=1
\end{array}$
Hence, the answer is the option 3.
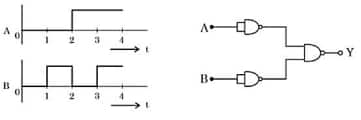
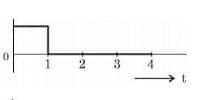
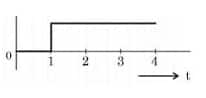
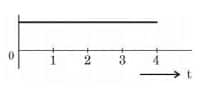
Question 20:
For the logic circuit shown, the output waveform at Y is:
1)
2)
3)

4)
Solution:
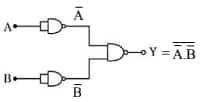 $\begin{aligned} y=\bar{A} \cdot \overline{\mathrm{~B}} \Rightarrow y & =\bar{A}+\bar{B} \\ y & =\mathrm{A}+\mathrm{B}\end{aligned}$
$\begin{aligned} y=\bar{A} \cdot \overline{\mathrm{~B}} \Rightarrow y & =\bar{A}+\bar{B} \\ y & =\mathrm{A}+\mathrm{B}\end{aligned}$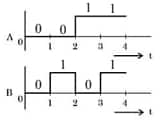
Hence, the answer is the option 2.
Question 21: A cylindrical rod of length 1 m and radius 4 cm is mounted vertically. It is subjected to a shear force of $10^5 \mathrm{~N}$ at the top. Considering infinitesimally small displacement in the upper edge, the angular displacement $\theta$ of the rod axis from its original position would be (shear moduli, $G=10^{10} \mathrm{~N} / \mathrm{m}^2$ )
1) $\frac{1}{4 \pi}$
2) $\frac{1}{40 \pi}$
3) $\frac{1}{2 \pi}$
4) (correct) $\frac{1}{160 \pi}$
Solution:
$\begin{aligned}
& \frac{F}{A}=G \theta \\
&\theta = \frac{10^5}{\pi 16 \times 10^{-4} \times 10^{10}} = \frac{1}{160 \pi}
\end{aligned}$
Hence, the answer is option (4).
Question 22: The fractional compression $\left(\frac{\Delta V}{V}\right)$ of water at a depth of 2.5 km below sea level is $\_\_\_\_$ $\%$. Given, the Bulk modulus of wat $=2 \times 10^9 \mathrm{Nm}^{-2}$, density of water $=10^3 \mathrm{~kg} \mathrm{~m}^{-3}$, acceleration due to gravity $=\mathrm{g}=10 \mathrm{~ms}^{-2}$.
1) 1.75
2) 1.0
3) 1.5
4) (correct) 1.25
Solution:
The pressure is, $P=\rho g h$
$\therefore \mathrm{B}=\frac{\rho \mathrm{gh}}{\left(\frac{\Delta \mathrm{~V}}{\mathrm{~V}}\right)}$
$\begin{aligned}
\frac{\Delta \mathrm{V}}{\mathrm{~V}} \times 100 & =\frac{\rho \mathrm{gh}}{\mathrm{~B}} \times 100 \\
& =\frac{1000 \times 10 \times 2.5 \times 10^3}{2 \times 10^9} \times 100 \% \\
& =1.25 \%
\end{aligned}$
Hence, the answer is option (4).
Question 23: A wire of length ' $L$ ' and radius ' $r$ ' is clamped rigidly at one end. When the other end of the wire is pulled by a force $f$, its length increases by ' $l$ '. Another wire of the same material of length ' $2 L$ ' and radius ' $2 r$ ' is pulled by a force ' $2 f$ '. Then the increase in its length will be :
1) $l / 2$
2) $4 l$
3) (correct) $l$
4) $2 l$
Solution:
By Hooke's law,
$\begin{aligned}
& Y=\frac{\mathrm{FL}}{\mathrm{~A} \Delta \mathrm{l}} \\
& \Delta \mathrm{l} \propto \frac{\mathrm{FL}}{\mathrm{~A}} \\
& \frac{\Delta \mathrm{l}_2}{\Delta \mathrm{l}_1}=\frac{\mathrm{F}_2 \mathrm{~L}_2}{\mathrm{~F}_1 \mathrm{~L}_1} \times \frac{\mathrm{A}_1}{\mathrm{~A}_2} \\
& =\frac{2 \mathrm{f} \times 2 \mathrm{~L}}{\mathrm{f} \times \mathrm{L}} \times \frac{\pi(\mathrm{r})^2}{\pi(2 \mathrm{r})^2} \\
& \Delta \mathrm{l}_1=\Delta \mathrm{l}_2 \\
& \Delta \mathrm{l}_2=l
\end{aligned}$
Hence, the answer is option (3).
Question 24: The elongation of a wire on the surface of the earth is $10^{-4} \mathrm{~m}$. The same wire of the same dimensions is elongated $6 \times 10^{-5} \mathrm{~m}$ on another planet. The acceleration due to gravity on the planet will be $\_\_\_\_$ $\mathrm{ms}^{-2}$. (Take acceleration due to gravity on the surface of the earth $=10 \mathrm{~ms}^{-2}$ )
1) (correct) 6
2) 7
3) 5
4) 4
Solution:
For a given material, Y, there will be a constant
$\begin{aligned}
& \Delta l_E=10^{-4} \mathrm{~m} \\
& \Delta l_p=6 \times 10^{-5} \mathrm{~m} \mid \mathrm{g}_P \rightarrow \text { acceleration due to gravity on planet } \\
& \mathrm{Y}=\frac{\mathrm{mg}}{\mathrm{~A}} \times \frac{1}{\Delta \mathrm{l}} \\
& \mathrm{~g} \propto \Delta \mathrm{l} \\
& \frac{\mathrm{~g}_{\mathrm{E}}}{\mathrm{~g}_{\mathrm{p}}}=\frac{\Delta \mathrm{l}_{\mathrm{E}}}{\Delta \mathrm{l}_{\mathrm{P}}} \\
& \frac{10}{\mathrm{~g}_{\mathrm{p}}}=\frac{10^{-4}}{6 \times 10^{-5}} \Rightarrow \mathrm{~g}_{\mathrm{p}}=6 \frac{\mathrm{~m}}{\mathrm{~s}^2}
\end{aligned}$
Hence, the answer is (6).
Question 25: A uniform metallic wire is elongated by 0.04 m when subjected to a linear force $F$. The elongation, if its length and diameter are doubled and subjected to the same force will be $\_\_\_\_$ cm .
1) 1
2) (correct) 2
3) 3
4) 4
Solution:
$\begin{aligned}
& \frac{\Delta \ell}{L}=\frac{\mathrm{F}}{\mathrm{Y} \cdot \mathrm{~A}} \cdot \\
& \Delta \ell=\frac{\mathrm{F} L}{\mathrm{Y} \cdot \pi \mathrm{r}^2} \\
& \Delta \ell \propto \frac{\ell}{\mathrm{r}^2} \\
& \frac{\Delta \ell_2}{\Delta \ell_1}=\left(\frac{\ell_2}{\ell_1}\right)\left(\frac{\mathrm{r}_1}{\mathrm{r}_2}\right)^2=(2)\left(\frac{1}{2}\right)^2=\frac{1}{2} \\
& \Rightarrow \Delta \mathrm{l}_2=\frac{\Delta l_1}{2}=\frac{0.04}{2}=0.02 \mathrm{~m}=2 \mathrm{~cm}
\end{aligned}$
Hence, the answer is option (2).
Frequently Asked Questions (FAQs)
Focusing on repeated types of questions and topics is a very good way of strategy because, one, the absolute same question may not come; but, the JEE MAINS constantly tests a set of core fundamental concepts. By knowing and mastering the high-frequency topics.
Not magic, but certainly helps boost your chances. Scoring over 90 is indicative of getting ~22-24 questions correct which can be achieved as a combination of:
Excel in High-Yield Topics: acquire a most significant share of marks with these secure sources.
Adequate Coverage of the Syllabus: The other chapters cannot be left completely untouched, as they may have easy questions that will also count for the grand total.
Examination Skills: Time management, accuracy, and avoiding negative marks.
The JEE Main 80/20 rule suggests 80% of your exam score comes from 20% of the syllabus, meaning focusing on high-weightage, frequently tested topics yields the best results, not trying to cover everything equally.
To score 90+ marks in JEE Main Physics:
Understand basic concepts from NCERT thoroughly.
Prioritize high-weightage chapters such as Modern Physics, Optics, and Electricity and Magnetism.
Regularly solve previous year questions and JEE Main mock tests.
A good rule of thumb is a 70-30 rule during your revision phase.
70% of your self-study time should be given to mastering, revising, and practicing problems from these high-yield topics.
Beyond that, 30% should be spent on the remaining syllabus so that you could attempt less-confident questions from anywhere in the paper.
Popular Courses and Specializations
List of colleges accepting JEE Main
Browse Engineering Colleges by State
Questions related to JEE Main
On Question asked by student community
Usha Mittal of Technology has no AI quota officially. please contact the college for any mangement quota seats.
decent chances actually as home state quota seats are 50%. allotments will depend on the JEE rank and not percentile though. in 2025, for female supernumerary it closed at 9286 rank while for open gen it closed at 5573.
So, would advise to use this tool to check the probable
yes you will. Ususally the return is within 7 days i it has failed at the gateway level which it seems to be. Please wait. You will get the money back
Slim chances as in 2025 the closing rank was 118 for SPA Delhi for B.Arch. You will need to wait for the rank list to come in April before getting a better picture. Please check https://engineering.careers360.com/jee-main-college-predictor for the predictions.
Check out https://engineering.careers360.com/jee-main-rank-predictor to know the probable rank
Hi Smita Sharma,
With 47 percentile in JEE Mains 2026, you might get rank around 7,00,000 plus which is very high. Check the link below for the Best engineering colleges available for you based on yours percentile.
Link 1: https://engineering.careers360.com/colleges/list-of-engineering-colleges-in-pune-accepting-jee-main
B.Tech/B.Arch Admissions OPEN
Among top 100 Universities Globally in the Times Higher Education (THE) Interdisciplinary Science Rankings 2026
Amrita University B.Tech 2026
ApplyRecognized as Institute of Eminence by Govt. of India | NAAC ‘A++’ Grade | Upto 75% Scholarships
Vignan's Deemed to be University B.Tech Admissions 2026
Apply70th University Ranked by NIRF | 80th Engineering Rank by NIRF | Accredited by NBA and NAAC A+
UPES B.Tech Admissions 2026
ApplyLast Date to Apply: 26th March | Ranked #43 among Engineering colleges in India by NIRF | Highest Package 1.3 CR , 100% Placements
MIT World Peace University B.Tech Admissions 2026
ApplyHighest CTC 44.14 LPA | UGC Approved | 1600+ Recruiters | 100% Placement
Manav Rachna-B.Tech Admissions 2026
ApplyNAAC A++ Grade | Recognized as Category-1 Deemed to be University by UGC | 41,000 + Alumni Imprints Globally