Amity University, Mumbai B.Tech Admissions 2025
ApplyRanked amongst top 3% universities globally (QS Rankings)
JEE Main: Differentiation and How To Calculate ‘e’
Updated on Apr 19, 2024 07:49 PM IST | #JEE Main
We all have come across the number ‘e’ while studying logarithm and calculus. This number is an irrational number like π, and is called Euler’s Number. Its value is 2.71828… and this sequence of digits never ends. So, how can we find this number and what is so special about this number?
A property that you must have studied in differentiation that stands out among all differentiation formulae is
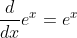
So, the differentiation of the function f(x) = ex, is this function itself. This makes this function unique. We will be using this property to calculate the number ‘e’. So, in all the calculations below, we will not use ‘e’ directly.
Let us start with the differentiation of a general exponential function, f(x) = 2x.
Using First Principle of Differentiation, we know that the differentiation of a function f(x) is
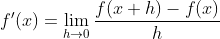
So, differentiation of f(x) = 2x will be
Now, when the value of the limit h→0 [(2h-1)/h] is calculated by putting different values of h that are very close to 0, we can see that the value of this expression approaches 0.693147…(Note that we are not directly using the value of this limit as ln(2), as the number ‘e’ and thus ln(x), which is log with the base ‘e’, is not yet known).
Also Read,
- JEE Main: How To Prepare At Home, Without Spending A Paisa
- Learn About Happy Hormones For NEET
- How To Help Your Child Nurture Their Mental Health
- VITEEE, JEE Main: One Prep, Ace Both
Let us see what values of [(2h-1)/h] we get by putting different values of h that are close to 0. We can use a calculator to find these values
When h = 0.001, [(2h-1)/h] = 0.6933…
When h = 0.0001, [(2h-1)/h] = 0.6931…
When h = 0.00000001, [(2h-1)/h] = 0.6931…
We can see that [(2h-1)/h] value approaches 0.6931…and hence
limit h→0 [(2h-1)/h]= 0.6931…
From equation (i):
f'(x) = 2x.(0.6931…)
So, differentiation of f(x) = 2x is of the form
f'(x) = Some constant. f(x)
Now if we do the same procedure with f(x) = 4x
When h = 0.001, [(4h-1)/h] = 1.3872…..
When h = 0.0001, [(4h-1)/h] = 1.38631…
When h = 0.00000001, [(4h-1)/h] = 1.38629…
So, limit h→0 [(4h-1)/h] = 1.38629…
And from (ii),
f'(x) = 4x . (1.38629…)
So, differentiation of f(x) = 4x is again of the form
f'(x) = Some constant. f(x)
In fact, we can do the same exercise for any positive real number a, and we will find that the differentiation of f(x) = ax equals some constant times ax
It can also be seen that the value of this constant keeps on increasing as the value of ‘a’ increases. For example
For a = 2, the constant we calculated was 0.6931…
For a = 4, the constant we calculated was 1.38629…
Similarly, for a = 5, the constant can be calculated to be 1.6094…
For a = 6, the constant is 1.7917…
So naturally we can ask ourselves the question that can we find a number ‘a’ for which this constant value equals 1, and thus differentiation of ax is 1. ax, meaning that the differentiation of the function ax is this function itself ( = ax)
After doing multiple hits and trials, this number can be found to be 2.71828. That is why we have the unique property,
d/dx(ex)= ex
Euler’s Number also finds applications in fields of mathematics other than calculus. One of the most important applications is in Complex Numbers. You must have come across the relation eiπ = - 1. Imaginary powers of e help us get the values of many trigonometric series which would otherwise be very difficult to prove using only the trigonometric relations. The number is also used in Finance (to calculate compound interest), to explain population growth of humans or microbes, to explain radioactive decay (which in turn is used to tell the age of ancient objects), etc.
Due to numerous applications, ‘e’ is the second most famous mathematical constant after π. We also celebrate ‘e-day’ on 7 February. This date is chosen as it is written as 2/7 in month/date format and the digits 2,7 represent the first two digits used in the value of ‘e’ (2.71…).
Articles
Certifications By Top Providers
Python For Beginners
Via PW Skills Java Fundamentals
Via Coding Ninjas Full-Stack Web Development
Via Masai School C-Based VLSI Design
Via Indian Institute of Technology Guwahati Python Basics
Via Accenture Structured Query Language Fundamentals
Via Accenture Explore Top Universities Across Globe
Georgia Institute of Technology, Atlanta
North Avenue, Atlanta, Georgia 30332University of Nottingham, Nottingham
University Park, Nottingham NG7 2RDUniversity of Strathclyde, Glasgow
16 Richmond St, Glasgow G1 1XQTexas A and M University, College Station
400 Bizzell St College Station, Texas 77843University College London, London
Gower Street, London, WC1E 6BTImperial College, London
South Kensington Campus, London SW7 2AZGRE Exam Dates 2025 in India: Check General & Subject Test Date
15 min ⋆ May 14, 2025 06:05 AM ISTUK Skilled Worker Visa 2025: Fees, Requirements and Process
9 min ⋆ Apr 10, 2025 11:04 AM ISTTruth About Medical Colleges in Philippines
5 min ⋆ May 14, 2025 05:05 AM ISTUK Govt Reduces Graduate Route Visa to 18 Months Under Immigration White Paper
5 min ⋆ May 14, 2025 04:05 AM ISTIELTS Speaking Preparation 2025: Tips & Tricks, Format, Strategies
12 min ⋆ May 13, 2025 14:05 PM ISTIELTS Reading Practice Test 5: Enhance Your Skills with Authentic Exercises
42 min ⋆ May 13, 2025 13:05 PM ISTPopular Courses and Specializations
List of colleges accepting JEE Main
Browse Engineering Colleges by State
Questions related to JEE Main
Have a question related to JEE Main ?
-
You can participate in CSAB Special Rounds after JoSAA if any lower NIT/IIIT or GFTI has CSE or related branches open for OBC-NCL + Female category.
-
Chances are very slim at your rank even in CSAB.
-
Private College Direct Admission
-
State Level Counselling Where Delhi Candidate Eligible (Private Colleges)
-
Try CUET UG 2025 for reputed Central Universities CSE programs.
Rohan 14 May,2025
-
Telangana Engineering colleges take admission through TS EAMCET, not JEE Mains (except some private universities).
-
You should participate in TS EAMCET counselling for state colleges.
- Few private universities/colleges may consider JEE Mains rank for management quota/direct admission .
Careers360 TS EAMCET College Predictor:
TS EAMCET College Predictor - Careers360
Rohan 14 May,2025
It is improbable that you would get admitted to SIT Lonavala's Computer Science and Engineering program with a JEE Main score of 62 percentile. CSE cutoffs have been far higher in other years, with closing ranks equal to percentiles exceeding 85–89. Other fields or universities with lower cutoffs could be worth looking into.
Swayam 13 May,2025
Sure, a jee main marks of 62.6% with 12 pass, you will admission in Sinhgad College of Engineering, Lonavala.
With you jee main marks you will be considered in All india quota or management quota. Also for some top branches you cannot choose with this mark but you can go with other branches like CS , civil etc..
All the best!!!
Admission with first class in JEE
Rubina Naseer 13 May,2025
With a 72 percentile in JEE Main 2025 and an expected 80%+ in your 12th board exams , securing admission to B.Tech in Computer Science & Engineering (CSE) at Guru Nanak Dev University (GNDU), Amritsar may be challenging.
A 72 percentile typically translates to an AIR between 250,000–300,000 , which is significantly higher than the previous year's closing ranks for CSE and related branches at GNDU.
- Consider applying for branches with higher closing ranks, such as Computer Engineering or Cyber Security , though admission may still be competitive.
- Look into other universities or colleges
- For more detailed information, you can visit GNDU's official admission page: GNDU Admissions (https://www.gnduadmissions.org/)
Rohan 13 May,2025
Popular JEE Main Questions
Explore Career Options (By Industry)
Flight Attendant
A flight attendant is a professional whose primary duty is to ensure the safety and comfort of passengers during an airline flight. An individual who is pursuing a career as a flight attendant is part of the cabin crew for the plane, a team of personnel who operate a commercial, business, or even military aircraft while travelling domestically or internationally.
An individual pursuing a career as a flight attendant is specially trained for the aircraft in which he or she works since passenger safety is their foremost concern. In this article, we will discuss how to become a flight attendant in India or how to become a flight attendant after graduation.
3 Jobs Available
Aerospace Engineer
An aerospace engineer designs, develops, tests, and maintains aircraft, spacecraft, and related systems. They apply physics and engineering principles to improve aerospace technologies, often working in aviation, defence, or space sectors. Key tasks include designing components, conducting tests, and performing research. A bachelor’s degree is essential, with higher roles requiring advanced study. The role demands analytical skills, technical knowledge, precision, and effective communication.
2 Jobs Available
Flight Engineer
A career in the aviation industry always sounds exciting. But, there is no scope for the slightest error as it may cost the lives of many people. A Flight Engineer role comes with the responsibility of monitoring the aircraft engine and control systems while in flight. Whenever the aircraft is away from the home station, he or she is required to perform pre-flight and post-flight inspections
2 Jobs Available
Aircrew officer
An Aircrew Officer operates and navigates aircraft, ensuring safe flights and compliance with aviation regulations. Key duties include managing flight systems, conducting pre- and post-flight checks, and adhering to safety standards. The role typically requires working five days a week, with around 120 flight hours monthly. Employment may be contractual or permanent, depending on the airline.
2 Jobs Available
Air Hostess
An air hostess, or flight attendant, ensures passenger safety and comfort during flights. Responsibilities include safety demonstrations, serving meals, managing the cabin, handling emergencies, and post-flight reporting. The role demands strong communication skills, a calm demeanour, and a service-oriented attitude. It offers opportunities to travel and work in the dynamic aviation and hospitality industry.
2 Jobs Available
Aeronautical Engineer
An aeronautical engineer designs, develops, tests, and maintains aircraft and related systems. They work on components like engines and wings, ensuring performance, safety, and efficiency. The role involves simulations, flight testing, research, and technological innovation to improve fuel efficiency and reduce noise. Aeronautical engineers collaborate with teams in aerospace companies, government agencies, or research institutions, requiring strong skills in physics, mathematics, and engineering principles.
2 Jobs Available
Safety Manager
A Safety Manager is a professional responsible for employee’s safety at work. He or she plans, implements and oversees the company’s employee safety. A Safety Manager ensures compliance and adherence to Occupational Health and Safety (OHS) guidelines.
2 Jobs Available
Airline Pilot
An airline pilot operates aircraft to transport passengers and cargo safely. Responsibilities include pre-flight planning, in-flight operations, team collaboration, and post-flight duties. Pilots work in varying schedules and environments, often with overnight layovers. The demand for airline pilots is expected to grow, driven by retirements and industry expansion. The role requires specialized training and adaptability.
1 Jobs Available
Welding Engineer
Welding Engineer Job Description: A Welding Engineer work involves managing welding projects and supervising welding teams. He or she is responsible for reviewing welding procedures, processes and documentation. A career as Welding Engineer involves conducting failure analyses and causes on welding issues.
5 Jobs Available
Transportation Planner
A career as Transportation Planner requires technical application of science and technology in engineering, particularly the concepts, equipment and technologies involved in the production of products and services. In fields like land use, infrastructure review, ecological standards and street design, he or she considers issues of health, environment and performance. A Transportation Planner assigns resources for implementing and designing programmes. He or she is responsible for assessing needs, preparing plans and forecasts and compliance with regulations.
3 Jobs Available
Environmental Engineer
Individuals who opt for a career as an environmental engineer are construction professionals who utilise the skills and knowledge of biology, soil science, chemistry and the concept of engineering to design and develop projects that serve as solutions to various environmental problems.
2 Jobs Available
Safety Manager
A Safety Manager is a professional responsible for employee’s safety at work. He or she plans, implements and oversees the company’s employee safety. A Safety Manager ensures compliance and adherence to Occupational Health and Safety (OHS) guidelines.
2 Jobs Available
Conservation Architect
A Conservation Architect is a professional responsible for conserving and restoring buildings or monuments having a historic value. He or she applies techniques to document and stabilise the object’s state without any further damage. A Conservation Architect restores the monuments and heritage buildings to bring them back to their original state.
2 Jobs Available
Structural Engineer
A Structural Engineer designs buildings, bridges, and other related structures. He or she analyzes the structures and makes sure the structures are strong enough to be used by the people. A career as a Structural Engineer requires working in the construction process. It comes under the civil engineering discipline. A Structure Engineer creates structural models with the help of computer-aided design software.
2 Jobs Available
Highway Engineer
Highway Engineer Job Description: A Highway Engineer is a civil engineer who specialises in planning and building thousands of miles of roads that support connectivity and allow transportation across the country. He or she ensures that traffic management schemes are effectively planned concerning economic sustainability and successful implementation.
2 Jobs Available
Field Surveyor
Are you searching for a Field Surveyor Job Description? A Field Surveyor is a professional responsible for conducting field surveys for various places or geographical conditions. He or she collects the required data and information as per the instructions given by senior officials.
2 Jobs Available
Geothermal Engineer
Individuals who opt for a career as geothermal engineers are the professionals involved in the processing of geothermal energy. The responsibilities of geothermal engineers may vary depending on the workplace location. Those who work in fields design facilities to process and distribute geothermal energy. They oversee the functioning of machinery used in the field.
3 Jobs Available
Geologist
A geologist attempts to comprehend the historical backdrop of the planet we live on, all the more likely to anticipate the future and clarify current events. He or she analyses the components, deployments, results, physical characteristics, and past of the planet. A geologist examines the landforms and landscapes of the earth in relation to the geology, climatic, and human processes that have shaped them.
A geologist studies earth procedures, for example, seismic tremors, avalanches, floods, and volcanic eruptions to review land and draw up safe structure plans. When he or she researches earth materials, explores metals and minerals, yet in addition search for oil, petroleum gas, water, and strategies to extricate these.
2 Jobs Available
Energy Performance Engineer
Energy efficiency engineering is a broad field of engineering which deals with energy efficiency, energy services, facility management, plant engineering, and sustainable energy resources. Energy efficiency engineering is one of the most recent engineering disciplines to emerge. The field combines the knowledge and understanding of physics, chemistry, and mathematics, with economic and environmental engineering practices. The main job of individuals who opt for a career as an energy performance engineer is to find the most efficient and sustainable path to operate buildings and manufacturing processes.
Individuals who opt for a career as energy performance engineers apply their understanding and knowledge to increase efficiency and further develop renewable sources of energy. The energy efficiency engineers also examine the use of energy in those procedures and suggest the ways in which systems can be improved.
2 Jobs Available
Petroleum Engineer
A career as a Petroleum engineer is concerned with activities related to producing petroleum. These products can be in the form of either crude oil or natural gas. Petroleum engineering also requires the exploration and refinement of petroleum resources. Therefore, a career as a petroleum engineer comes up with oil and gas onshore jobs. There are also desk jobs in the petroleum industry. In layman’s terms, a petroleum engineer is a person who finds the best way to drill and extract oil from oil wells. Individuals who opt for a career as petroleum engineer also tries to find new ways to extract oil in an efficient manner.
2 Jobs Available
Transportation Planner
A career as Transportation Planner requires technical application of science and technology in engineering, particularly the concepts, equipment and technologies involved in the production of products and services. In fields like land use, infrastructure review, ecological standards and street design, he or she considers issues of health, environment and performance. A Transportation Planner assigns resources for implementing and designing programmes. He or she is responsible for assessing needs, preparing plans and forecasts and compliance with regulations.
3 Jobs Available
Civil Engineer
A career as a civil engineer is of great importance for the infrastructural growth of the country. It is one of the most popular professions and there is great professional as well as personal growth in this civil engineering career path. There is job satisfaction in this civil engineering career path, but it also comes with a lot of stress, as there are multiple projects that need to be handled and have to be completed on time. Students should pursue physics, chemistry and mathematics in their 10+2 to become civil engineers.
2 Jobs Available
Transportation Engineer
A career as a Transportation Engineer is someone who takes care of people's safety. He or she is responsible for designing, planning and constructing a safe and secure transportation system. The transportation sector has seen a huge transformation and is growing day by day and improving every day.
As a Transport Engineer, he or she needs to solve complex problems such as accidents, costs, traffic flow, and statistics. A Transport Engineer also collaborates for projects with some other companies.
1 Jobs Available
Loco Pilot
A Loco Pilot operates trains, ensuring safe and timely transport of passengers or goods. Starting as an Assistant Loco Pilot, one can progress to senior roles with experience. The job demands technical knowledge, focus, and adherence to safety protocols. It involves coordination with train staff and may require working long hours under pressure.
2 Jobs Available
B.Tech/B.Arch Admissions OPEN
UPES B.Tech Admissions 2025
ApplyRanked #42 among Engineering colleges in India by NIRF | Highest Package 1.3 CR , 100% Placements | Last Date to Apply: 18th May
Jain University B.Tech Admissions 2025
Apply100% Placement Record | Highest CTC 54 LPA | NAAC A++ Accredited | Ranked #65 in India by NIRF Ranking 2024 | JEE & JET Scores Accepted
Graphic Era (Deemed to be University) Admissions 2025
ApplyNAAC A+ Grade | Among top 100 universities of India (NIRF 2024) | 40 crore+ scholarships distributed
Bharati Vidyapeeth B.Tech Admissions 2025
ApplyNAAC A++ Grade | Category-I Deemed to be University Grade by UGC
Pimpri Chinchwad University B.Tech Admissions
Apply1000+ Recruiters | 450+ Patents | 50000+ Alumni network
News and Notifications
May 14, 2025 - 03:44 PM IST
May 11, 2025 - 04:01 PM IST
May 04, 2025 - 12:20 PM IST
May 01, 2025 - 03:00 PM IST
April 30, 2025 - 06:46 PM IST
April 29, 2025 - 10:36 PM IST
April 28, 2025 - 11:48 AM IST
Stay up-to date with JEE Main News
Back to top