JEE Advanced Mathematics 2025 - Top Skipped, Wrongly Attempted and Correctly Solved Questions

JEE Advanced 2025 Mathematics Analysis - Paper 1 and Paper 2 Question-Wise Candidate’s Performance

The Mathematics section of JEE Advanced 2025 provides insights into how candidates performed across Paper 1 and Paper 2. A question-wise analysis highlights accuracy, difficulty levels, and common mistakes, helping aspirants identify their strengths and weakness for Maths preparation. Given below table highlighting the question-wise performance of candidates:

Most Skipped Mathematics Questions (High Non-Attempt %)

The most skipped questions in JEE Advanced Maths were primarily from topics like Matrices, 3D Geometry, Probability, and Integral Calculus. For example, in Paper 1, Q4 (Matrices) had a 72.11% skip rate, while in Paper 2, Q6 (Integral Calculus) was skipped by 78.55% of candidates.

Paper 1

Paper 2

From the given data, it is clear that a significant number of candidates chose to leave particular questions in both Paper 1and Paper 2 unattempted, shown in the statistics of Not Attempted and % Not Attempted. In Paper I, questions with the highest percentage of skipped responses were Q4 , Q5 and Q1 . The least skipped response was for Q2. Paper 2, on the other hand, had even higher skips, with Q6 being the most skipped question, touching 141,728 candidates, followed by Q3 and Q7. From this table it is clear that Paper 2 questions had a higher percentage of non attempts compared to Paper.

Detailed Concept-wise Analysis of JEE Advanced Mathematics 2025 Paper 1 & Paper 2 is given below:

JEE Advanced Maths Paper 2 Question 6

Question: Let $S$ denote the locus of the mid-points of those chords of the parabola $y^2=x$, such that the area of the region enclosed between the parabola and the chord is $\frac{4}{3}$. Let $\mathcal{R}$ denote the region lying in the first quadrant, enclosed by the parabola $y^2=x$, the curve $S$, and the lines $x=1$ and $x=4$.

Then which of the following statements is (are) TRUE?

1- $(4,\sqrt{3})\in S$ (Correct)

2- $(5,\sqrt{2})\in S$

3- Area of $R$ is $\frac{14}{3}-2\sqrt{3}$ (Correct)

4- Area of $R$ is $\frac{14}{3}-\sqrt{3}$

Correct Option:- 1 and 3

Solution:-

Given: The parabola is $y^2=x$

Let a chord of this parabola have midpoint $(h,k)$. The equation of the chord with given midpoint in terms of $T=S_1$ form is:

$yk-\frac{y+h}{2}=k^2-h$

$2ky-y^2-h=2k^2-2h$

Now, $A={\int }_{y_1}^{y_2}(2ky-2k^2+h0-y^2)dy=\frac{4}{3}$

$(k{y}^2+(h-2k^2)y-\frac{y^3}{3}{)}_{y_1}^{y_2}=\frac{4}{3}$

$(y_2-y_1)[k-2k+h-2k^2-\frac{1}{3}(4k^2-2k^2+h)]=\frac{4}{3}$

$(h-k^2{)}^{\frac{3}{2}}=1$

$h-k^2=1$

Thus, the locus $S$ is:
$x-y^2=1\Rightarrow y^2=x-1$

We'll check if these points lie on the line, by putting the values,

$(\sqrt{3}{)}^2=4-1$----True

But $5^2=\sqrt{2}-1$-----False,

Thus, point $(4,\sqrt{3})$ lies on the line, so Option 1 is correct.

Now find the area $\mathcal{R}$ enclosed between:
- Parabola $y^2=x\Rightarrow y=\sqrt{x}$
- Curve $S$: $y=\sqrt{x-1}$
- Vertical lines $x=1$ and $x=4$

The area of region $\mathcal{R}$ is:

$A={\int }_1^4(\sqrt{x}-\sqrt{x-1})dx$

$={[\frac{2}{3}{x}^{3/2}-\frac{2}{3}(x-1{)}^{3/2}]}_1^4=\frac{2}{3}[8-3\sqrt{3}-1]=\frac{2}{3}(7-3\sqrt{3})$

$\mathcal{R}=\frac{14}{3}-2\sqrt{3}$
Option 3 is also correct

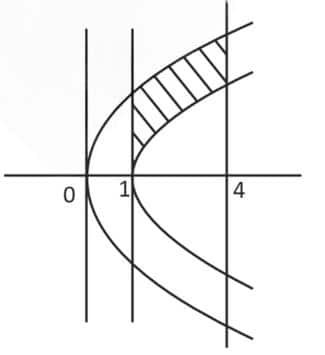
Hence, the correct answers are option 1,3.

Why most students skip this question?

Double Concept

• In this question two ideas are mixed using parameters for the parabola and then solving with definite integration. Many students get confused about which method to start with. Some try direct integration without using parameters, which takes much longer. Because it mixes topics, many students prefer to avoid it.

Confusion with “Region in First Quadrant”

• When students read this part, they have to imagine the shapes of the curves $y^2=x$ and $x=y^2+1$ on a graph. Many get confused about which curve lies above or below the other.

• They spend extra time just trying to draw and compare them, which take up so much time in the final area calculation.

Two-Stage Question Format

• Even after finding the locus $S$, the problem is not finished. It also asks to check which points lie on $S$ and then to find the area of another region $\mathcal{R}$.

• Under exam pressure, students like quick, one-step answers. Questions with many steps feel too long and time-consuming.

Answer-Type (Multiple Correct)

• The question has options (A–D) where more than one can be correct. Students know they must be fully sure, because partial answers don’t give marks.

• With so many steps: locus, integration, and checking points, the chances of making a mistake are high, so many skip it.

Indirect Parametrisation Trick

• The simple method is to use parameters for the parabola: $x=p^2,y=p$. Students who don’t remember this try solving directly with equations of lines and midpoints. That becomes very messy and wastes time. Missing this trick makes the question too heavy.

In short, the question looks too lengthy, indirect and too integration-heavy at first sight. It involves two different conceptual tricks (parametrisation of a parabola, simplification of the area formula). It is multi-stage with multiple correct options, raising the risk of wasted time and no marks.

Most Wrongly Attempted Mathematics Questions (High Wrong Response %)

The Mathematics JEE Advanced 2025 analysis also highlights the biggest trap questions. For instance, Paper 2 Question 13 Complex Numbers saw 72.99% wrong attempts. These questions appeared straightforward but were full of pitfalls, showcasing common mistakes in JEE Advanced Mathematics like sign errors, misusing formulas, or ignoring principal values.

Paper 1

Paper 2

The analysis of wrongly attempted questions reveals that certain problems acted as traps widely attempted but rarely solved correctly. For instance, Q13 (Paper 2) saw 72.99% wrong responses, while Q10 (Paper 2) had 69.77% wrong responses. Similarly, Q11 (Paper 1) and Q8 (Paper 1) recorded 69.48% and 69.04% wrong responses, respectively. The common pattern across these questions was that the % Not Attempted values remained moderate (around 23–27%), meaning most students felt confident enough to try them. However, the % Full Marks was dismally low — only 1.44% for Q10 (Paper 2) and 2.81% for Q13 (Paper 2). This mismatch between high attempts and high wrong responses shows that these questions were either conceptually tricky, calculation-intensive, or designed with distractor options that lured students into errors. While questions like Q12 (Paper 1) with 40.02% not attempted but only 51.42% wrong responses, show that students consciously avoided tougher problems, reducing the wrong-attempt ratio.

JEE Advanced Maths Paper 2 Question 13

Question: For a non-zero complex number $z$, let $\arg (z)$ denote the principal argument of $z$, with $-\pi <\arg (z)\le \pi$. Let $\omega$ be the cube root of unity for which $0<\arg (\omega )<\pi$. Let

$\alpha =\arg (\sum _{n=1}^{2025}(-\omega {)}^n)$

Then the value of $\frac{3\alpha }{\pi }$ is__________.

Correct Answer:- -2

Solution:

Let $r=-\omega$. Then

$S=\sum _{n=1}^{2025}(-\omega {)}^n=\sum _{n=1}^{2025}{r}^n=\frac{r(1-r^{2025})}{1-r}=\frac{-\omega (1-(-\omega {)}^{2025})}{1+\omega }$

Note $(-\omega {)}^3=-1$, so

$(-\omega {)}^{2025}=((-\omega {)}^3{)}^{675}=(-1{)}^{675}=-1$

Thus $1-(-\omega {)}^{2025}=1-(-1)=2$, and

$S=\frac{-\omega \cdot 2}{1+\omega }=\frac{-2\omega }{1+\omega }$

Using $1+\omega +{\omega }^2=0$ gives $1+\omega =-{\omega }^2$Hence

$S=\frac{-2\omega }{-{\omega }^2}=2\frac{\omega }{{\omega }^2}=2{\omega }^2$

Now ${\omega }^2=e^{4\pi i/3}$ has principal argument $\arg ({\omega }^2)=-\frac{2\pi }{3}$. Therefore

$\alpha =\arg (S)=\arg (2{\omega }^2)=\arg ({\omega }^2)=-\frac{2\pi }{3}$

Finally, $\frac{3\alpha }{\pi }=\frac{3\cdot (-\frac{2\pi }{3})}{\pi }=-2$

Hence, the correct answer is -2.

Why many students got it wrong?

• Which $\omega$? There are two non-real cube roots of unity. If you take the wrong one, your signs flip or changes and you get the wrong answer.

• Period confusion: Some think $(-\omega {)}^n$ repeats every 3 steps, but it actually takes 6 steps to repeat. This gives wrong grouping or cancellation.

• Geometric series mistakes: In the formula $\sum r^n$, many students put the wrong minus sign or denominator, so the result comes out wrong.

• Forgetting principal argument rules: Even if they get the complex sum correct, they sometimes write the angle as $4\pi /3$ instead of the main value $-2\pi /3$. This changes ${\displaystyle \frac{3\alpha }{\pi }}$ a lot.

• Ignoring simple simplifications. The identity $1+\omega +{\omega }^2=0$ makes the problem short. Without it, students do long steps and get lost.

• Not checking the power pattern. Since 2025 is a multiple of 3 (and of $3\times 675$), the powers follow a simple cycle. Many do not notice or expand it too much.

Most Correctly Solved Mathematics Questions (Higher Accuracy)

Interestingly, certain questions were the most solved questions in JEE Advanced Maths 2025. For example, Paper 1 Q15 (Maxima & Minima) had 37.69% full marks, while Paper 2 Q9 (Differential Equations) had 28.93%. These were largely direct applications of textbook concepts, explaining their higher accuracy.

Paper 1

Paper 2

JEE Advanced Maths Paper 1 Question 15

Question: Let $\mathbb{R}$ denote the set of all real numbers. For a real number x, let [x] denote the greatest integer less than or equal to x. Let n denote a natural number.

Match each entry in List-I to the correct entry in List-II and choose the correct option.

1) $(\mathrm{P})⟶(1)(\mathrm{Q})⟶(3)(\mathrm{R})⟶(2)(\mathrm{S})⟶$ (5)
2) $(\mathrm{P})⟶(2)(\mathrm{Q})⟶(1)(\mathrm{R})⟶(4)(\mathrm{S})⟶(3)$ (Correct)
3) $(\mathrm{P})⟶(5)(\mathrm{Q})⟶(1)(\mathrm{R})⟶(4)(\mathrm{S})⟶(3)$
4) $(\mathrm{P})⟶(2)(\mathrm{Q})⟶(3)(\mathrm{R})⟶(1)(\mathrm{S})⟶(5)$

Correct Option:- 2

Solution:

Given: $\{\begin{array}{ll}(P)& f(x)=\left[\frac{10x^3-45x^2+60x+35}{n}\right],x\in [1,2]\\ (Q)& g(x)=(2n^2-13n-15)(x^3+3x),x\in \mathbb{R}\\ (R)& h(x)=(x^2-9{)}^n(x^2+2x+3),n>5\\ (S)& I(x)=\sum _{k=0}^4(\sin |x-k|+\cos |x-k+\frac{1}{2}|),x\in \mathbb{R}\end{array}$

(P): Find minimum $n$ so that $f(x)$ is continuous on $[1,2]$.

Define $g(x)=10x^3-45x^2+60x+35$
Calculate derivative: $g^{\prime }(x)=30x^2-90x+60=30(x^2-3x+2)=30(x-1)(x-2)$

On $[1,2]$, since $(x-1)(x-2)\le 0$, $g(x)$ is decreasing.

Evaluate: $f(1)=\left[\frac{g(1)}{n}\right]=\left[\frac{60}{n}\right],f(2)=\left[\frac{g(2)}{n}\right]=\left[\frac{55}{n}\right]$

For continuity, $f(1)=f(2)$:
$\left[\frac{60}{n}\right]=[\frac{55}{n}\rfloor$

Try $n=9$: $\left[\frac{60}{9}\right]=6,\left[\frac{55}{9}\right]=6$

So minimum $n=9$.

$(P)\to (2)$

(Q): Find minimum $n$ such that $g(x)=(2n^2-13n-15)(x^3+3x)$ is increasing on $\mathbb{R}$.

$g^{\prime }(x)=(2n^2-13n-15)(3x^2+3)=3(2n^2-13n-15)(x^2+1)$

Since $x^2+1>0$, sign depends on $2n^2-13n-15$.

Set: $2n^2-13n-15>0$

Solve quadratic inequality:
$2n^2-13n-15=0⟹n=\frac{13\pm \sqrt{169+120}}{4}=\frac{13\pm 17}{4}$

Roots:
$n=7.5,n=-1$

Since $n$ natural, $n\ge 8$ for positivity.

$(Q)\to (1)$

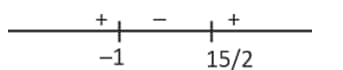
(R): Find smallest natural $n>5$ so that $x=3$ is local minimum of $h(x)=(x^2-9{)}^n(x^2+2x+3)$

Note: $h(3)=(9-9{)}^n(9+6+3)=0$

For local minimum at $x=3$, $h(x)$ should increase on both sides near 3 for some $n$.

Check behavior near 3:

- For $x>3$, $(x^2-9)>0$,
- For $x<3$, $(x^2-9)<0$.

Since the factor $(x^2-9{)}^n$ changes sign depending on $n$ even or odd:

$n=6$ (even and $>5$) ensures local minimum at $x=3$.

$(R)\to (4)$

(S): Find number of points $x_0$ where $I(x)=\sum _{k=0}^4(\sin |x-k|+\cos |x-k+\frac{1}{2}|)$
is NOT differentiable.

- $\sin |x-a|$ is not differentiable at $x=a$.
- $\cos |x-a|$ is differentiable everywhere.

Non-differentiable points are at $x=k$ for $k=0,1,2,3,4$.

Number of such points = 5.

$(S)\to (3)$

(P) : 9 (List-II (2))

(Q) : 8 (List-II (1))

(R) : 6 (List-II (4))

(S) : 5 (List-II (3))

Final matching: $(P)\to (2),(Q)\to (1),(R)\to (4),(S)\to (3).$

Hence, the answer is option 2.

Why most students solved it correctly

Each part is straight from the textbook and can be checked in one line.

• (Q) comes down to checking the sign of a quadratic; the derivative is always positive because $3x^2+3>0$.

• (R) is about behaviour near a root: $(x^2-9{)}^n$ has factor $(x-3{)}^n$; if $n$ is even, it makes a local minimum.

• (S) is counting points where $\sin |x-k|$ is not differentiable at $x=k$ (there are five such $k$).

• (P) is just checking values of a cubic in a small interval; its range is $[55,60]$ and you only test multiples.

No long algebra or tough integrals are needed

• Each part just needs a short step or one inequality.

Numbers are simple

• Intervals like $[55,60]$, the set $0,1,2,3,4$, and easy quadratic roots make checking quick and easy.

Checks are clear and fast

• For monotonicity, check the coefficient sign; for local min, check even/odd power; for non-differentiability, check absolute-value breaks; for floor continuity, just see if an integer multiple lies in the interval. All can be done quickly under exam pressure.

In short, the question was straight from the textbook ideas. Each part needed only one quick check - sign of a quadratic, odd–even power rule, sharp corner of sine, or small range of a cubic. Numbers were easy, intervals small, and steps short. So students could solve it fast without long algebra.

Distribution of Total Marks in Aggregate (all, qualified and allotted candidates)

For all candidates, the aggregate marks distribution shows the overall performance in JEE Advanced 2025. Given below this information using charts:

For All Candidates

For Qualified Candidates

For Seat Allotted Candidates

JEE Advanced 2025 Mathematics: Most Difficult Questions

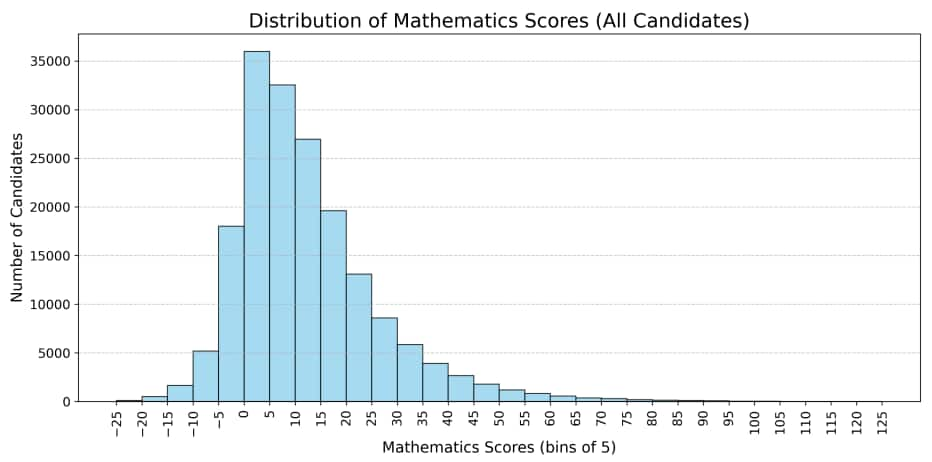
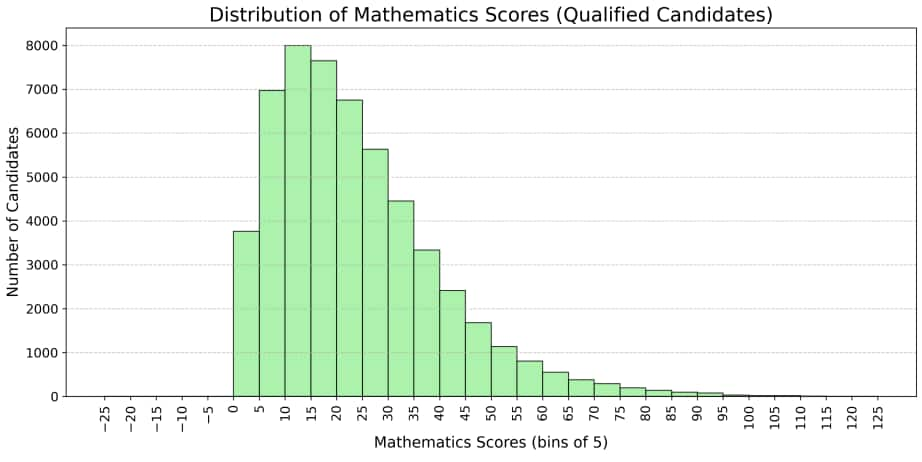
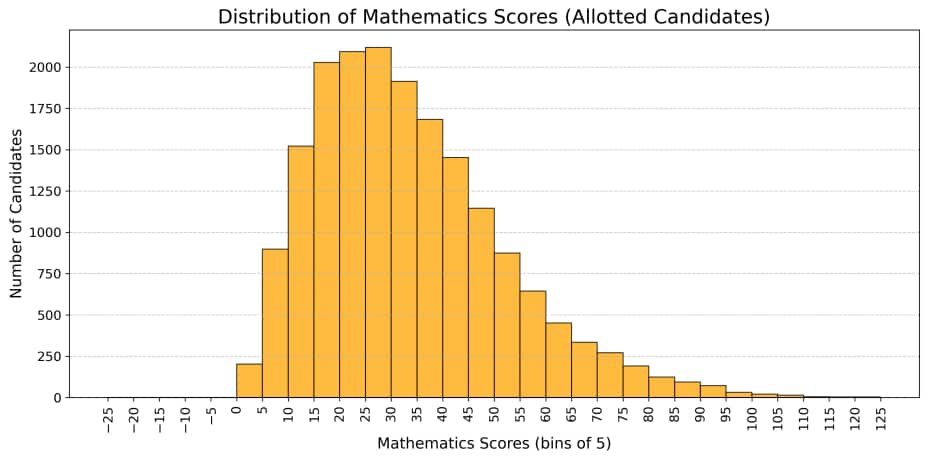
The JEE Advanced 2025 question trends clearly show that the toughest problems were those with:

• Low % full marks,

• Moderate attempts, but

• Very high wrong response percentages.

Paper 1

The most difficult questions in JEE Advanced Maths Paper 1 (Q8, Q9, Q10, Q11, Q12) are difficult due to a mix of high wrong response rates and very low full marks percentages. Questions like Q8 and Q11 had nearly 70% wrong attempts, showing that while most students tried them, the trap-based nature or multiple-case logic led to errors. Q10 stood out with the lowest full marks (1.44%), suggesting it required multi-step solving where even small mistakes caused failure. Q9 and Q12 had higher non-attempt rates (34-40%), reflecting the intimidating or lengthy nature of these problems, though Q12 still had slightly better full marks, indicating it was solvable with strong conceptual clarity. Overall, these questions combined conceptual depth, calculation intensity, and cleverly designed traps, making them the toughest of the paper and pushing up their difficulty index values.

Paper 2

The toughest questions in JEE Advanced Maths Paper 2 (Q13, Q16, Q10, Q12, Q15) stood out due to their very low full marks percentages coupled with extremely high wrong response rates. Q13, from Complex Numbers and Quadratic Equations, was the most difficult with only 2.81% full marks and a massive 72.99% wrong response, showing that while most students attempted it, the conceptual traps and tricky algebra led to widespread failure. Q16 (Integral Calculus) also saw only 3.7% full marks and 65.12% wrong responses, indicating lengthy solving or integration pitfalls. Q10 and Q12, from Binomial Theorem and Vector Algebra, respectively, had slightly better full marks (6.64% and 8.6%) but still suffered from nearly 70% wrong attempts, reflecting complex application-based logic. Q15 (Trigonometry) showed the highest success of this set with 9.62% full marks, yet more than 64% wrong responses highlight it was not straightforward. Overall, these questions combined multi-step solving, conceptual depth, and trap-heavy design, making them the most challenging of Paper 2 and greatly influencing its overall toughness index.

With this analysis, aspirants can identify the most skipped questions in JEE Advanced Maths, avoid the common mistakes in JEE Advanced Mathematics, and practice more on the most attempted questions in JEE Advanced Maths 2025 that often become traps. By focusing on these JEE Advanced 2025 question trends and revising the JEE Advanced Maths solved questions 2025, candidates can strengthen their exam strategy.