Top 25 Repeated JEE Mains Questions to Score 90+ in Physics

High-Scoring Chapters of JEE Main Physics to Score 90+

JEE Main Physics can be done really well if you keep studying such chapters that have consistently carried high weightage in past years and repeated PYQ patterns, and you can score above 90. The table below shows the most scoring Physics chapters for Physics PYQs to score 90+ in JEE Main, expected question frequency, and scoring potential.

Physics Top Highest Repeated Concepts of the Last Five Years

Top 25 Repeated JEE Mains Questions in Physics

The questions are based on highly repeated concepts in the previous few years, concepts that appear almost every year in JEE Main Physics with maximum scoring potential if prepared well.

Question 1: A particle is projected at an angle of $30^{\circ}$ from horizontal at a speed of $60 \mathrm{~m} / \mathrm{s}$. The height traversed by the particle in the first second is $h_0$ and height traversed in the last second, before it reaches the maximum height, is $h_1$. Then $h_0: h_1$ is________.
$\left[\right.$ Take, $\left.g=10 \mathrm{~m} / \mathrm{s}^2\right]$

Solution:

Given Data:
Initial velocity: $u=60 \mathrm{~m} / \mathrm{s}$
Angle of projection: $\theta=30^{\circ}$
Acceleration due to gravity: $g=10 \mathrm{~m} / \mathrm{s}^2$
We need to find the ratio of:
Height traversed in the first second $\left(h_0\right)$
Height traversed in the last second before reaching maximum height $\left(h_1\right)$
Step 1: Find the Vertical Component of Velocity
The initial vertical velocity:

$
u_y=u \sin 30^{\circ}=60 \times \frac{1}{2}=30 \mathrm{~m} / \mathrm{s}
$

Step 2: Find the Time to Reach Maximum Height
At the maximum height, the vertical velocity becomes zero:

$
\begin{aligned}
& v_y=u_y-g t \\
& 0=30-10 t \\
& t=\frac{30}{10}=3 \mathrm{~s}
\end{aligned}
$

So, the total time to reach maximum height is 3 seconds.
Step 3: Height Traversed in the First Second $\left(h_0\right)$

Using the equation of motion:

$
h_0=u_y t+\frac{1}{2} a_y t^2
$

For $t=1 \mathrm{~s}$ :

$
h_0=(30 \times 1)+\frac{1}{2}\left(-10 \times 1^2\right)
$

$
h_0=30-5=25 \mathrm{~m}
$

Step 4: Height Traversed in the Last Second $\left(h_1\right)$
The height traversed in the last second before reaching maximum height is given by:

$
h_1=v_y t-\frac{1}{2} a_y t^2
$

$
\mathrm{h}_1=0-\frac{1}{2}\left(-10 \times 1^2\right)=5 \mathrm{~m}
$

Step 5: Find the Ratio $h_0: h_1$

$
h_0: h_1=25: 5=5: 1
$

Hence, the answer is 5.

Question 2: The angle of projection for a projectile to have same horizontal range and maximum height is :
1) $\tan ^{-1}(2)$

2) (correct) $\tan ^{-1}(4)$

3) $\tan ^{-1}\left(\frac{1}{4}\right)$

4) $\tan ^{-1}\left(\frac{1}{2}\right)$

Solution:

$\mathrm{\begin{aligned} & \frac{u^2 \sin 2 \theta}{g}=\frac{u^2 \sin ^2 \theta}{2 g} \\ & 4 \sin \theta \cos \theta=\sin ^2 \theta \\ & 4=\tan \theta\end{aligned}}$

$\theta=\tan ^{-1}(4)$

Hence, the answer is the option (2).

Question 3: The maximum height reached by a projectile is 64 m. If the initial velocity is halved, the new maximum height of the projectile is ______ m.

Solution:

$ \mathrm{H}_{\max }=\frac{\mathrm{u}^2 \sin ^2 \theta}{2 \mathrm{~g}} \\ $

$ \frac{\mathrm{H}_{1 \max }}{\mathrm{H}_{2 \max }}=\frac{\mathrm{u}_1^2}{\mathrm{u}_2^2} $

$\frac{64}{\mathrm{H}_{2 \max }}=\frac{\mathrm{u}^2}{(\mathrm{u} / 2)^2} $

$ \mathrm{H}_{2 \max }=16 \mathrm{~m}$

Hence the answer is 16.

Question 4: The initial speed of a projectile fired from ground is $u$ At the highest point during its motion, the speed of projectile is $\frac{\sqrt{3}}{2} u$. The time o flight of the projectile is :
1) $\frac{2 \mathrm{u}}{\mathrm{g}}$
2) $\frac{\mathrm{u}}{2 \mathrm{~g}}$
3) $\frac{\sqrt{3} u}{g}$
4) (correct) u

Solution :

At the highest point -

$\begin{aligned}
& \mathrm{u} \cos \theta=\frac{\sqrt{3} \mathrm{u}}{2} \\
& \theta=30 \\
& \mathrm{~T}=\frac{2 \mathrm{u} \sin \theta}{\mathrm{~g}}=\frac{\mathrm{u}}{\mathrm{~g}}
\end{aligned}$
Hence, the answer is the option (4).

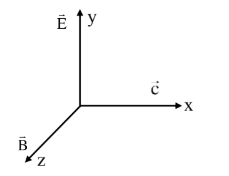
Question 5: A plane electromagnetic wave propagates along the $+x$ direction in free space. The components of the electric field, $\vec{E}$ and magnetic field, $\vec{B}$ vectors associated with the wave in Cartesian frame are:
1) $\mathrm{E}_y, \mathrm{~B}_{\mathrm{x}}$
2) (correct) $\mathrm{E}_{\mathrm{y}}, \mathrm{B}_{\mathrm{z}}$
3) $E_x, B_y$
4) $\mathrm{E}_z, \mathrm{~B}_y$

Solution:

Direction of propagation$
=\overrightarrow{\mathrm{E}} \times \overrightarrow{\mathrm{B}}
$

$E \rightarrow y, B \rightarrow z, c \rightarrow x$

$\hat{\mathrm{E}} \times \hat{\mathrm{B}}=\hat{\mathrm{j}} \times \hat{\mathrm{k}}=\hat{\mathrm{i}}=\hat{\mathrm{c}}$

Hence, the answer is the option (2).

Question 6: The magnetic field of an E.M. wave is given by

$\overrightarrow{\mathrm{B}}=\left(\frac{\sqrt{3}}{2} \hat{\mathrm{i}}+\frac{1}{2} \hat{\mathrm{j}}\right) 30 \sin \left[\omega\left(\mathrm{t}-\frac{\mathrm{z}}{\mathrm{c}}\right)\right] \text { (S.I. Units) }$

The corresponding electric field in SI units is :

1) $\overrightarrow{\mathrm{E}}=\left(\frac{1}{2} \hat{\mathrm{i}}-\frac{\sqrt{3}}{2} \hat{\mathrm{j}}\right) 30 \mathrm{c} \sin \left[\omega\left(\mathrm{t}-\frac{\mathrm{z}}{\mathrm{c}}\right)\right]$

2) $\overrightarrow{\mathrm{E}}=\left(\frac{3}{4} \hat{\mathrm{i}}+\frac{1}{4} \hat{\mathrm{j}}\right) 30 \mathrm{c} \cos \left[\omega\left(\mathrm{t}-\frac{\mathrm{z}}{\mathrm{c}}\right)\right]$

3) $\overrightarrow{\mathrm{E}}=\left(\frac{1}{2} \hat{\mathrm{i}}+\frac{\sqrt{3}}{2} \hat{\mathrm{j}}\right) 30 \mathrm{c} \sin \left[\omega\left(\mathrm{t}+\frac{\mathrm{z}}{\mathrm{c}}\right)\right]$

4) $\overrightarrow{\mathrm{E}}=\left(\frac{\sqrt{3}}{2} \hat{\mathrm{i}}-\frac{1}{2} \hat{\mathrm{j}}\right) 30 \mathrm{c} \sin \left[\omega\left(\mathrm{t}+\frac{\mathrm{z}}{\mathrm{c}}\right)\right]$

Solution:

$\begin{aligned} & \vec{B}=\left(\frac{\sqrt{3}}{2} \hat{i}+\frac{1}{2} \hat{j}\right) 30 \sin \left[\omega\left(t-\frac{z}{c}\right)\right] \\ & \vec{E}=\vec{B} \times \overrightarrow{\mathrm{c}} \text { and } E_0 = B_0 c \\ & \hat{E} = \left(\frac{\sqrt{3}}{2}(-\hat{j})+\frac{1}{2} \hat{i}\right) \\ & E_0=30 c \\ & \vec{E}=\left(\frac{1}{2} \hat{i}-\frac{\sqrt{3}}{2} \hat{j}\right) 30 c \sin \left[\omega\left(t-\frac{z}{c}\right)\right]\end{aligned}$

Hence, the answer is the option (1).

Question 7: The magnetic field in a plane electromagnetic wave is $B_y=\left(3.5 \times 10^{-7}\right) \sin \left(1.5 \times 10^3 x+0.5 \times 10^{11} \mathrm{t}\right) \mathrm{T}$. The corresponding electric field will be
1) $\mathrm{E}_{\mathrm{y}}=1.17 \sin \left(1.5 \times 10^3 \mathrm{x}+0.5 \times 10^{11} \mathrm{t}\right) \mathrm{Vm}^{-1}$

2) (correct) $\mathrm{E}_{\mathrm{z}}=105 \sin \left(1.5 \times 10^3 \mathrm{x}+0.5 \times 10^{11} \mathrm{t}\right) \mathrm{Vm}^{-1}$

3) $\mathrm{E}_{\mathrm{z}}=1.17 \sin \left(1.5 \times 10^3 \mathrm{x}+0.5 \times 10^{11} \mathrm{t}\right) \mathrm{Vm}^{-1}$

4) $\mathrm{E}_{\mathrm{y}}=10.5 \sin \left(1.5 \times 10^3 \mathrm{x}+0.5 \times 10^{11} \mathrm{t}\right) \mathrm{Vm}^{-1}$

Solution :

$\begin{aligned}
& \mathrm{E}_0=\mathrm{B}_0 \mathrm{C} \\
& \mathrm{E}_0=3 \times 10^8 \times\left(3.5 \times 10^{-7}\right) \sin \left(1.5 \times 10^3 \mathrm{x}+0.5 \times 10^{11} \mathrm{t}\right) \\
& \mathrm{E}_0=105 \sin \left(1.5 \times 10^3 \mathrm{x}+0.5 \times 10^{11} \mathrm{t}\right) \mathrm{Vm}^{-1}
\end{aligned}$
Hence, the answer is the option (2).

Question 8: A plane electromagnetic wave of frequency 20 MHz travels in free space along the $+x$ direction. At a particular point in space and time, the electric field vector of the wave is $\mathrm{E}_{\mathrm{y}}=9.3 \mathrm{Vm}^{-1}$. Then, the magnetic field vector of the wave at that point is-
1) $\mathrm{B}_{\mathrm{z}}=9.3 \times 10^{-8} \mathrm{~T} $

2) $\mathrm{B}_{\mathrm{z}}=1.55 \times 10^{-8} \mathrm{~T}$

3) $\mathrm{B}_{\mathrm{z}}=6.2 \times 10^{-8} \mathrm{~T}$

4) (correct) $\mathrm{B}_{\mathrm{z}}=3.1 \times 10^{-8} \mathrm{~T}$

Solution:

$\begin{aligned}
& \mathrm{E}=\mathrm{Bc} \\
& 9.3=\mathrm{B} \times 3 \times 10^8 \\
& \mathrm{~B}=\frac{9.3}{3 \times 10^8}=3.1 \times 10^{-8} \mathrm{~T}
\end{aligned}$
Hence, the answer is the option (4).

Question 9:Find the equivalent resistance between two ends of the following circuit.

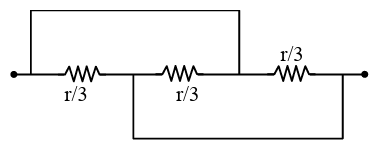
1) r
2) $\frac{r}{6}$
3) (correct) $\frac{r}{9}$
4) $\frac{r}{3}$

Solution:

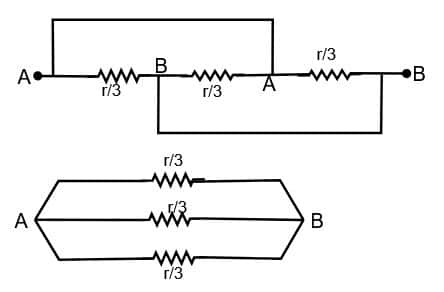
All are in parallel

$R_{e q}=\frac{r / 3}{3}=r / 9$

Hence, the answer is the option (3).

Question 10:

The equivalent resistance of the following network is ________ $\Omega$

Solution:

$6 \Omega$ is short circuit

$
R_{e q}=3 \times \frac{1}{3}=1 \Omega
$

Hence, the answer is 1.

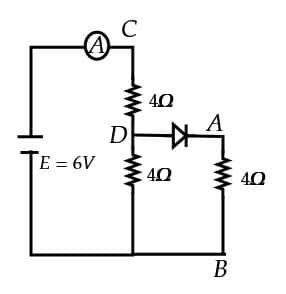
Question 11: Refer to the circuit diagram given in the figure, which of the following observation are correct?
A. The total resistance of the circuit is $6 \Omega$.
B. Current in Ammeter is 1 A
C. Potential across AB is 4 volts.
D. Potential across CD is 4 volts:
E. The total resistance of the circuit is $8 \Omega$.

Choose the correct answer from the options given below:

1) (correct) A, B and D only
2) A, C and D only
3) B, C and E only
4) A, B and C only

Solution:

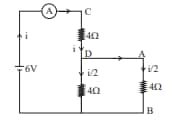
$\begin{aligned} & \text { Req }=4+\frac{4 \times 4}{4+4} \\ & =6 \Omega \\ & i=\frac{6}{6} \\ & =1 \mathrm{~A} \\ & V_{A B}=\frac{i}{2} \times R \\ & =\frac{1}{2} \times 4 \quad=2 \mathrm{~V}\end{aligned}$

$\begin{aligned} & V_{C D}=i R \\ & =1 \times 4 \\ & =4 \mathrm{~V}\end{aligned}$

Hence, the answer is option (1).

Question 12: In the given circuit 'a' is an arbitrary constant. The value of m for which the equivalent circuit resistance is minimum, will be $\sqrt{\frac{x}{2}}$. The value of $x$ is

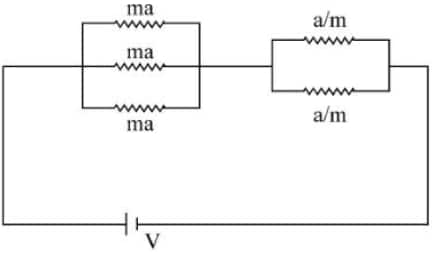
Solution:

$
\begin{aligned}
\text { Req } & =\frac{\mathrm{ma}}{3}+\frac{(\mathrm{a} / \mathrm{m})}{2} \\
& =\frac{\mathrm{ma}}{3}+\frac{\mathrm{a}}{2 \mathrm{~m}} \\
& =\frac{2 \mathrm{~m}^2 \mathrm{a}+3 \mathrm{a}}{6 \mathrm{~m}} \\
& =\frac{\mathrm{ma}}{3}+\frac{\mathrm{a}}{2 \mathrm{~m}}
\end{aligned}
$

For $\mathrm{R}_{\text {eq }}$ to be minimum,

$
\begin{aligned}
& \frac{\mathrm{dReq}}{\mathrm{dm}}=0 \\
& \frac{\mathrm{a}}{3}-\frac{\mathrm{a}}{2 \mathrm{~m}^2}=0 \\
& \frac{\mathrm{a}}{3}=\frac{\mathrm{a}}{2 \mathrm{~m}^2} \Rightarrow \mathrm{~m}^2=\frac{3}{2} \\
& \quad \mathrm{~m}=\sqrt{\frac{3}{2}}
\end{aligned}
$

Hence, the answer is option (3).

Question 13: A proton of mass ' $\mathrm{m}_{\mathrm{p}}$ ' has the same energy as that of a photon of wavelength' $\lambda$ '. If the proton is moving at a non-relativistic speed, then the ratio of its de Broglie wavelength to the wavelength of the photon is.
1) $\frac{1}{c} \sqrt{\frac{2 E}{m_p}}$

2) $\frac{1}{c} \sqrt{\frac{E}{m_p}}$

3) (correct $\frac{1}{c} \sqrt{\frac{E}{2 m_p}}$

4) $\frac{1}{2 c} \sqrt{\frac{E}{m_p}}$

Solution:

E is missing in the question but considering E as energy, the solution will be

$\begin{aligned}
& \mathrm{E}_{\text {photon }}=\frac{\mathrm{hc}}{\lambda}=\mathrm{E} ; \mathrm{E}_{\text {proton }}=\frac{1}{2} \mathrm{~m}_{\mathrm{p}} \mathrm{v}^2=\mathrm{E} \\
& \frac{\lambda_{\text {proton }}}{\lambda_{\text {photon }}}=\frac{\mathrm{h} / \mathrm{p}}{\mathrm{hc} / \mathrm{E}}=\frac{\mathrm{h} / \sqrt{2 \mathrm{~m}_{\mathrm{p}} \mathrm{E}}}{\mathrm{hc} / \mathrm{E}} \\
& =\frac{\mathrm{E}}{\mathrm{c} \sqrt{2 \mathrm{~m}_{\mathrm{p}} \mathrm{E}}} \\
& \frac{\lambda_{\text {proton }}}{\lambda_{\text {photon }}}=\frac{1}{\mathrm{c}} \sqrt{\frac{\mathrm{E}}{2 \mathrm{~m}_{\mathrm{p}}}}
\end{aligned}$

Hence, the answer is the option (3).

Question 14: A proton and an electron are associated with same de-Broglie wavelength. The ratio of their kinetic energies is : (Assume $\mathrm{h}=6.63 \times 10^{-34} \mathrm{~J} \mathrm{~s}, \mathrm{~m}_{\mathrm{e}}=9.0 \times 10^{-31} \mathrm{~kg}$ and $\mathrm{m}_{\mathrm{p}}=1836$ times $\mathrm{m}_{\mathrm{e}}$ )
1) (correct) $1: 1836$

2) $1: \frac{1}{1836}$

3) $1: \frac{1}{\sqrt{1836}}$

4) $1: \sqrt{1836}$

Solution:

$\lambda$ is same for both

$\begin{aligned}
& P=\frac{h}{\lambda} \text { same for both } \\
& P=\sqrt{2 \mathrm{mK}}
\end{aligned}$

Hence,

$\begin{aligned}
\mathrm{K} & \propto \frac{1}{\mathrm{~m}} \\
\Rightarrow & \frac{\mathrm{KE}_{\mathrm{p}}}{\mathrm{KE}_{\mathrm{e}}}=\frac{\mathrm{m}_{\mathrm{e}}}{\mathrm{~m}_{\mathrm{p}}}=\frac{1}{1836}
\end{aligned}$

Hence, the answer is option (1).

Question 15: A proton and an electron have the same de Broglie wavelength. If $K_p$ and $K_e$ be the kinetic energies of proton and electron respectively. Then choose the correct relation :
1) $\mathrm{K}_{\mathrm{p}}>\mathrm{K}_{\mathrm{e}}{ }^2$

2) $K_p=K_e$

3) $\mathrm{K}_{\mathrm{p}}=\mathrm{K}_{\mathrm{e}}{ }^2$

4) (correct) $\mathrm{K}_{\mathrm{p}}<\mathrm{K}_{\mathrm{e}}$

Solution:

De Broglie wavelength of proton \& electron $=\lambda$
$
\begin{aligned}
& \because \lambda=\frac{\mathrm{h}}{\mathrm{p}} \\
& \therefore \mathrm{p}_{\text {proton }}=\mathrm{p}_{\text {electron }} \\
& \because \mathrm{KE}=\frac{\mathrm{p}^2}{2 \mathrm{~m}} \\
& \therefore \mathrm{KE}_{\text {proton }}<\mathrm{KE}_{\text {electron }} \\
& {\left[\mathrm{K}_{\mathrm{p}}<\mathrm{K}_{\mathrm{e}}\right]}
\end{aligned}
$

Hence, the answer is option (4).

Question 16: An $\alpha$-particle, a proton and an electron have the same kinetic energy. Which one of the following is correct in the case of their de-Broglie wavelength:
1) (correct) $\lambda_\alpha<\lambda_{\mathrm{p}}<\lambda_{\mathrm{e}}$

2) $\lambda_\alpha=\lambda_{\mathrm{p}}=\lambda_{\mathrm{e}}$

3) $\lambda_\alpha>\lambda_{\mathrm{p}}>\lambda_{\mathrm{e}}$

4) $\lambda_\alpha>\lambda_{\mathrm{p}}<\lambda_{\mathrm{e}}$

Solution:

$\begin{aligned}
& \lambda=\frac{\mathrm{h}}{\sqrt{2 \mathrm{mkE}}} \alpha \frac{1}{\sqrt{\mathrm{~m}}} \\
& \mathrm{~m}_{\mathrm{a}}>\mathrm{m}_{\mathrm{p}}>\mathrm{m}_{\mathrm{e}} \\
& \therefore \lambda_{\mathrm{a}}<\lambda_{\mathrm{p}}<\lambda_{\mathrm{e}}
\end{aligned}$
Hence, the answer is the option (1).

Question 17: The output of the circuit is low (zero) for :

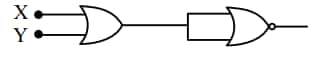
(A) $\mathrm{X}=0, \mathrm{Y}=0$ (B) $X=0, Y=1$
(C) $\mathrm{X}=1, \mathrm{Y}=0$ (D) $\mathrm{X}=1, \mathrm{Y}=1$

Choose the correct answer from the options given below :

1) (A), (C) and (D) only
2) (A), (B) and (C) only
3) (correct) (B), (C) and (D) only
4) (A), (B) and (D) only

Solution:

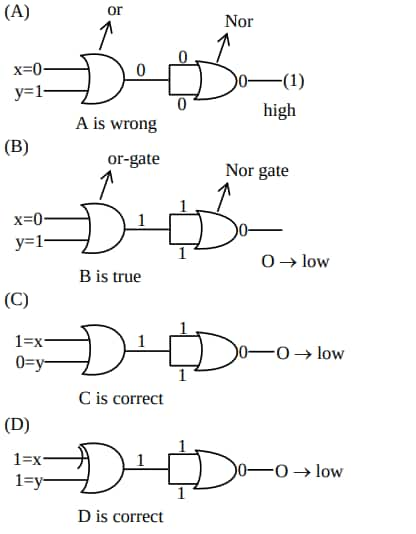
Hence, the answer is the option (3).

Question 18: The output (Y) of logic circuit given below is 0 only when :

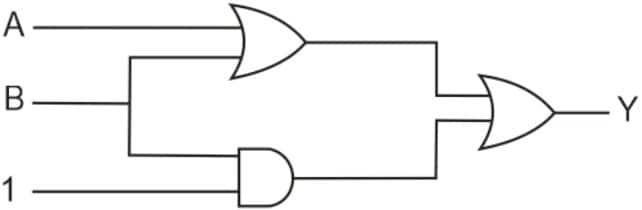
1) $A=1, B=0$

2) (correct) $A=0, B=0$

3) $A=1, B=1$

4) $A=0, B=1$

Solution:

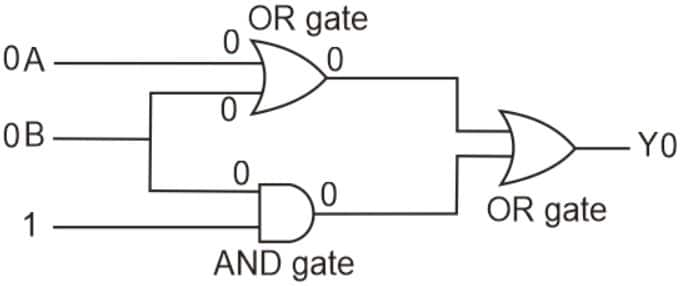
Hence, the answer is the option 2.

Question 19: For the following circuit and given inputs A and B, choose the correct option for output 'Y'

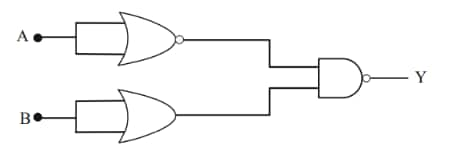
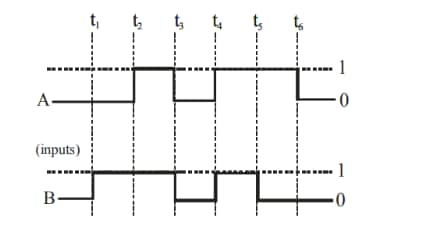
1)

2)

3)

4)

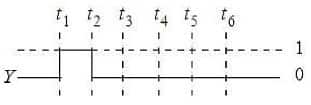
Solution:

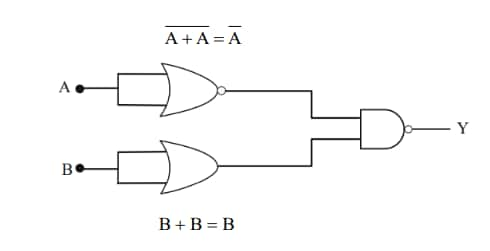
Output,

$\mathrm{y}=\overline{\overline{\mathrm{A}} \cdot \mathrm{B}}=\overline{\overline{\mathrm{A}}}+\overline{\mathrm{B}} = A + \overline{B}$

$\begin{array}{ll}
\mathrm{t}_1 \text { to } \mathrm{t}_2, & \mathrm{~A}=0, \mathrm{~B}=1, \mathrm{Y}=0 \\
\mathrm{t}_2 \text { to } \mathrm{t}_3 & \mathrm{~A}=1, \mathrm{~B}=1, \mathrm{Y}=1 \\
\mathrm{t}_3 \text { to } \mathrm{t}_4 & \mathrm{~A}=0, \mathrm{~B}=0, \mathrm{Y}=1 \\
\mathrm{t}_4 \text { to } \mathrm{t}_5, & \mathrm{~A}=1, \mathrm{~B}=1, \mathrm{Y}=1 \\
\mathrm{t}_5 \text { to } \mathrm{t}_6, & \mathrm{~A}=1, \mathrm{~B}=0, \mathrm{Y}=1 \\
\mathrm{After}~\mathrm{t}_6, & \mathrm{~A}=0, \mathrm{~B}=0, \mathrm{Y}=1
\end{array}$

Hence, the answer is the option 3.

Question 20:

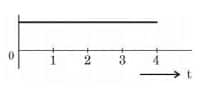
For the logic circuit shown, the output waveform at Y is:

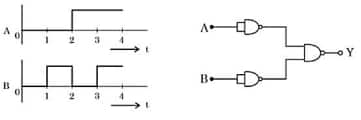
1)

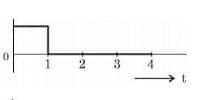
2)

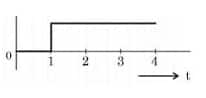
3)

4)

Solution:

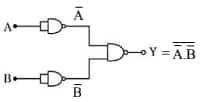$\begin{aligned} y=\bar{A} \cdot \overline{\mathrm{~B}} \Rightarrow y & =\bar{A}+\bar{B} \\ y & =\mathrm{A}+\mathrm{B}\end{aligned}$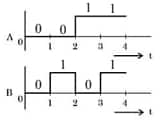

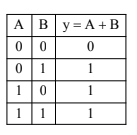
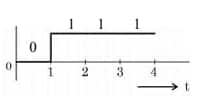
Hence, the answer is the option 2.

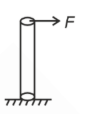
Question 21: A cylindrical rod of length 1 m and radius 4 cm is mounted vertically. It is subjected to a shear force of $10^5 \mathrm{~N}$ at the top. Considering infinitesimally small displacement in the upper edge, the angular displacement $\theta$ of the rod axis from its original position would be (shear moduli, $G=10^{10} \mathrm{~N} / \mathrm{m}^2$ )
1) $\frac{1}{4 \pi}$

2) $\frac{1}{40 \pi}$

3) $\frac{1}{2 \pi}$

4) (correct) $\frac{1}{160 \pi}$

Solution:

$\begin{aligned}
& \frac{F}{A}=G \theta \\
&\theta = \frac{10^5}{\pi 16 \times 10^{-4} \times 10^{10}} = \frac{1}{160 \pi}
\end{aligned}$

Hence, the answer is option (4).

Question 22: The fractional compression $\left(\frac{\Delta V}{V}\right)$ of water at a depth of 2.5 km below sea level is $\_\_\_\_$ $\%$. Given, the Bulk modulus of wat $=2 \times 10^9 \mathrm{Nm}^{-2}$, density of water $=10^3 \mathrm{~kg} \mathrm{~m}^{-3}$, acceleration due to gravity $=\mathrm{g}=10 \mathrm{~ms}^{-2}$.
1) 1.75
2) 1.0
3) 1.5
4) (correct) 1.25

Solution:

The pressure is, $P=\rho g h$

$\therefore \mathrm{B}=\frac{\rho \mathrm{gh}}{\left(\frac{\Delta \mathrm{~V}}{\mathrm{~V}}\right)}$
$\begin{aligned}
\frac{\Delta \mathrm{V}}{\mathrm{~V}} \times 100 & =\frac{\rho \mathrm{gh}}{\mathrm{~B}} \times 100 \\
& =\frac{1000 \times 10 \times 2.5 \times 10^3}{2 \times 10^9} \times 100 \% \\
& =1.25 \%
\end{aligned}$
Hence, the answer is option (4).

Question 23: A wire of length ' $L$ ' and radius ' $r$ ' is clamped rigidly at one end. When the other end of the wire is pulled by a force $f$, its length increases by ' $l$ '. Another wire of the same material of length ' $2 L$ ' and radius ' $2 r$ ' is pulled by a force ' $2 f$ '. Then the increase in its length will be :
1) $l / 2$
2) $4 l$
3) (correct) $l$
4) $2 l$

Solution:

By Hooke's law,

$\begin{aligned}
& Y=\frac{\mathrm{FL}}{\mathrm{~A} \Delta \mathrm{l}} \\
& \Delta \mathrm{l} \propto \frac{\mathrm{FL}}{\mathrm{~A}} \\
& \frac{\Delta \mathrm{l}_2}{\Delta \mathrm{l}_1}=\frac{\mathrm{F}_2 \mathrm{~L}_2}{\mathrm{~F}_1 \mathrm{~L}_1} \times \frac{\mathrm{A}_1}{\mathrm{~A}_2} \\
& =\frac{2 \mathrm{f} \times 2 \mathrm{~L}}{\mathrm{f} \times \mathrm{L}} \times \frac{\pi(\mathrm{r})^2}{\pi(2 \mathrm{r})^2} \\
& \Delta \mathrm{l}_1=\Delta \mathrm{l}_2 \\
& \Delta \mathrm{l}_2=l
\end{aligned}$
Hence, the answer is option (3).

Question 24: The elongation of a wire on the surface of the earth is $10^{-4} \mathrm{~m}$. The same wire of the same dimensions is elongated $6 \times 10^{-5} \mathrm{~m}$ on another planet. The acceleration due to gravity on the planet will be $\_\_\_\_$ $\mathrm{ms}^{-2}$. (Take acceleration due to gravity on the surface of the earth $=10 \mathrm{~ms}^{-2}$ )
1) (correct) 6
2) 7
3) 5
4) 4

Solution:

For a given material, Y, there will be a constant

$\begin{aligned}
& \Delta l_E=10^{-4} \mathrm{~m} \\
& \Delta l_p=6 \times 10^{-5} \mathrm{~m} \mid \mathrm{g}_P \rightarrow \text { acceleration due to gravity on planet } \\
& \mathrm{Y}=\frac{\mathrm{mg}}{\mathrm{~A}} \times \frac{1}{\Delta \mathrm{l}} \\
& \mathrm{~g} \propto \Delta \mathrm{l} \\
& \frac{\mathrm{~g}_{\mathrm{E}}}{\mathrm{~g}_{\mathrm{p}}}=\frac{\Delta \mathrm{l}_{\mathrm{E}}}{\Delta \mathrm{l}_{\mathrm{P}}} \\
& \frac{10}{\mathrm{~g}_{\mathrm{p}}}=\frac{10^{-4}}{6 \times 10^{-5}} \Rightarrow \mathrm{~g}_{\mathrm{p}}=6 \frac{\mathrm{~m}}{\mathrm{~s}^2}
\end{aligned}$

Hence, the answer is (6).

Question 25: A uniform metallic wire is elongated by 0.04 m when subjected to a linear force $F$. The elongation, if its length and diameter are doubled and subjected to the same force will be $\_\_\_\_$ cm .
1) 1
2) (correct) 2
3) 3
4) 4

Solution:

$\begin{aligned}
& \frac{\Delta \ell}{L}=\frac{\mathrm{F}}{\mathrm{Y} \cdot \mathrm{~A}} \cdot \\
& \Delta \ell=\frac{\mathrm{F} L}{\mathrm{Y} \cdot \pi \mathrm{r}^2} \\
& \Delta \ell \propto \frac{\ell}{\mathrm{r}^2} \\
& \frac{\Delta \ell_2}{\Delta \ell_1}=\left(\frac{\ell_2}{\ell_1}\right)\left(\frac{\mathrm{r}_1}{\mathrm{r}_2}\right)^2=(2)\left(\frac{1}{2}\right)^2=\frac{1}{2} \\
& \Rightarrow \Delta \mathrm{l}_2=\frac{\Delta l_1}{2}=\frac{0.04}{2}=0.02 \mathrm{~m}=2 \mathrm{~cm}
\end{aligned}$

Hence, the answer is option (2).