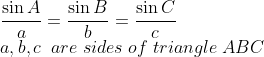BITSAT 2025 Formulas for Physics, Chemistry, Maths
BITSAT Formulas for PCM: BITSAT is a crucial exam for every student who wishes to join the top private engineering college in India - BITS Pilani. It is considered a moderate to difficult exam, inclined more on the difficult side. To properly prepare for the BITS Admission Test (BITSAT), one needs to understand concepts thoroughly along with having a good command of formulas. The exam encompasses three significant subjects - Physics, Chemistry, and Mathematics (PCM) - each one overflowing with key formulas you must remember and use promptly. Within this article, we’ll simplify a few of the BITSAT formulas for Physics, Chemistry, and Maths to help you optimize your study efforts for the BITSAT 2026 exam. Let's dive in!
This Story also Contains
- Benefits of Knowing BITSAT Formulas for PCM
- BITSAT 2026 Formulas for Physics
- BITSAT 2026 Formulas for Chemistry
- BITSAT 2026 Formulas for Maths

Benefits of Knowing BITSAT Formulas for PCM
The BITSAT examination is famed for its fast and rapid format. During the 180-minute exam, you have to answer 150 multiple-choice questions, giving you very little time to calculate formulas during the test. Remembering major formulas can cut down on precious time, raise accuracy, and help you compete effectively. There exists a unique collection of equations for each subject that allows for fast problem resolution, allowing you to concentrate more on understanding their application. We should analyse the important formulas for each area.
Also Read:
BITSAT 2026 Formulas for Physics
Physics in BITSAT is heavy on numerical problems, requiring a good grasp of formulas. Understanding these formulas will help you solve problems on topics like Mechanics, Electricity, Magnetism, and Optics. Here are some important BITSAT Physics formulas:
Newton’s Second Law:
Newton’s second law of motion:-
It states that the acceleration of the particle measured from an inertial frame is given by the (vector) sum of all the forces acting on the particle divided by its mass (only when mass is constant), i.e.,
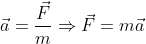
2.To cross river in the shortest path
condition ( velocity of boat along river flow must be zero)
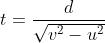
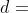 width of river
width of river
v = Speed of Boat w.r.t. river
u = speed of river
3. 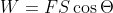
Ohm’s Law:
In a conductor, if all external physical conditions like temperature and pressure are kept constant the Current flowing through a conductor is directly proportional to the Potential difference across two ends.
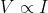
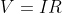
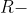 Electric Resistance
Electric Resistance
The graph between V and I
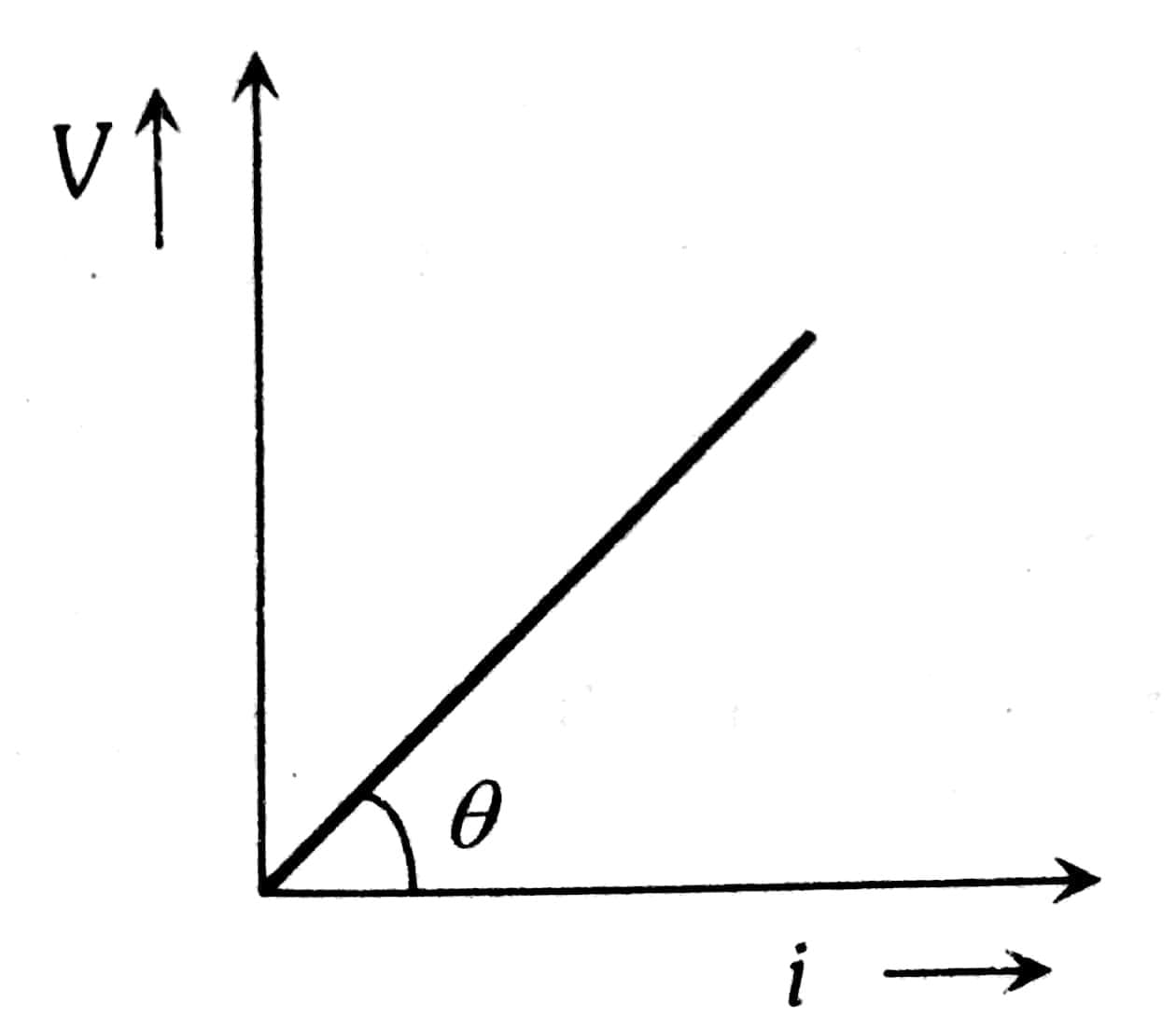
The slope gives the resistance
The graph between V and I at different temperatures
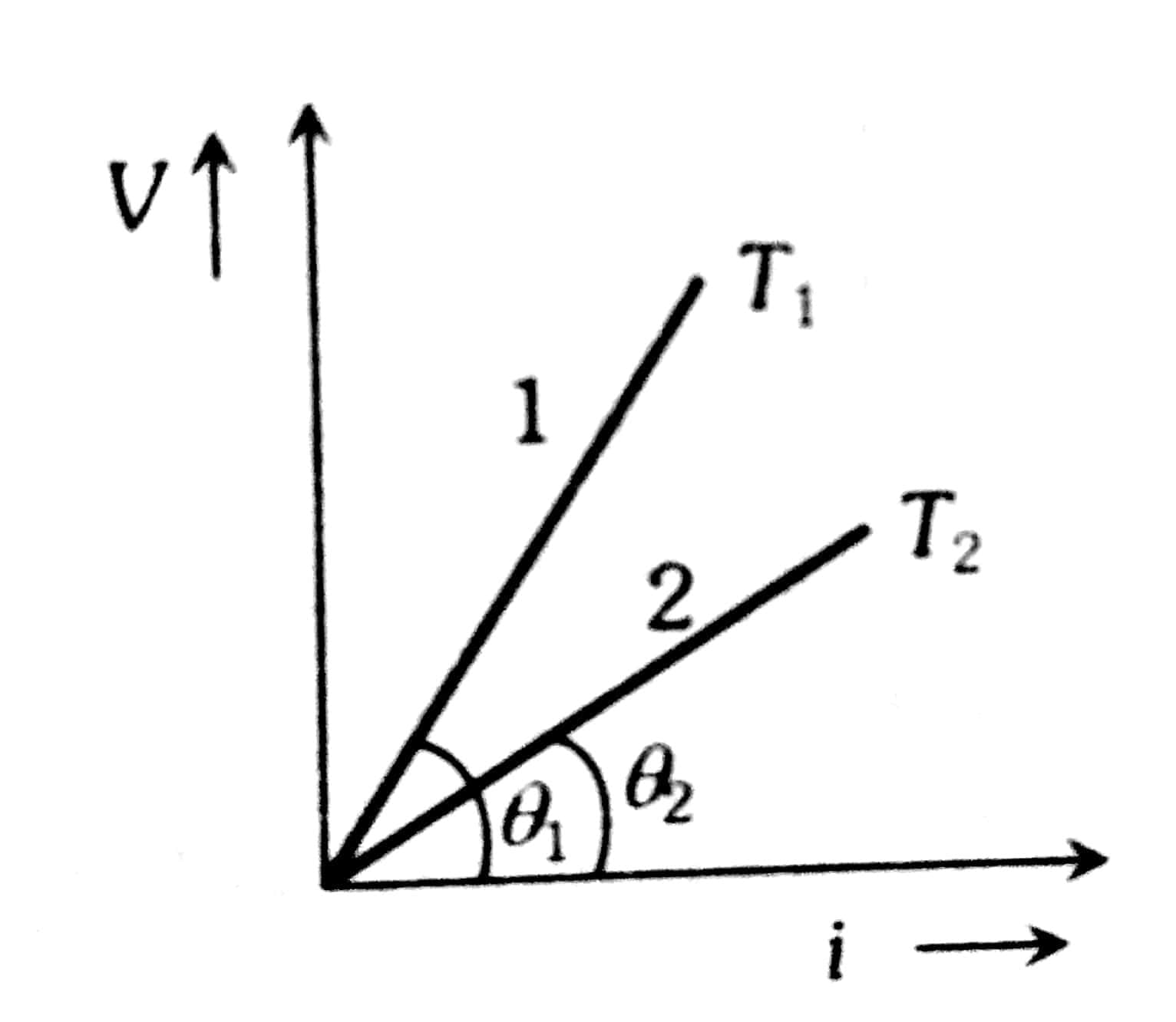
Here T1>T2. The resistance of a conductor increases with increase in temperature
Kinematic Equations: For uniform acceleration:
Equation of motions | There are three equations of motion
Formula
V = Final velocity u = Initial velocity A = acceleration T = time
Formula
Formula
Where
n= |
the Net electric field is -
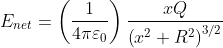
Lens Formula: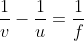
(f is the focal length, v is the image distance, and u is the object distance)
BITSAT 2026 Formulas for Chemistry
Chemical formulas are of great significance in BITSAT; most of the numerical problems in Physical Chemistry will either make or mar your performance. Chemistry and both Inorganic and Organic Chemistry in particular will also test you on some principles and reaction mechanisms. Here are some BITSAT Chemistry formulas that will come in handy:
Ideal Gas Equation:
|
Pressure × Volume equals to number of moles × Gas constant × Temperature
Graham’s Law of Diffusion
According to it "At constant temperature and pressure, the rate of diffusion of a gas is inversely proportional to the square root of its density or molecular weight". It is applicable only at low pressure.
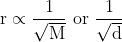 Here r = rate of diffusion or effusion of a gas or liquid. M and d are the molecular weight and density respectively.
Here r = rate of diffusion or effusion of a gas or liquid. M and d are the molecular weight and density respectively.
For any two gases, the ratio of the rate of diffusion at constant pressure and temperature can be shown as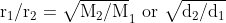 Hence diffusion or effusion of a gas or gaseous mixture is directly proportional to the pressure difference of the two sides and is inversely proportional to the square root of the gas or mixture effusing or diffusing out.
Hence diffusion or effusion of a gas or gaseous mixture is directly proportional to the pressure difference of the two sides and is inversely proportional to the square root of the gas or mixture effusing or diffusing out.
Some Other Relation Based on Graham’s law
As r = V/t = Volume/time, thus: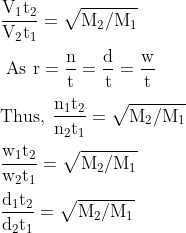
Arrhenius Equation:
We know that the first-order equation is given as follows:
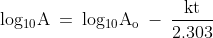
But there are other forms of rate law also available that we use for different purposes. These forms are mentioned below:
Use to solve numericals:
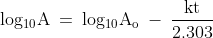
![\mathrm{\Rightarrow log_{10}\left [ \frac{A_{o}}{A} \right]\: =\: \frac{kt}{2.303}}](https://cache.careers360.mobi/media/articles/uploads/froala_editor/images/2024/11/5/1730807915350.png)
![\mathrm{Thus, t\: =\: \frac{2.303}{k}\, log_{10}\left [ \frac{A_{o}}{A} \right]}](https://cache.careers360.mobi/media/articles/uploads/froala_editor/images/2024/11/5/1730807917238.png)
Exponential form:
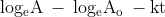
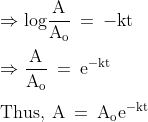 This equation is also known as exponential form.
This equation is also known as exponential form.The rate constant is shown by this formula; Rate constant = Frequency factor × Exponential factor related to activation energy
Boyle’s Law:

k1 is the proportionality constant whose value depends upon the following factors.
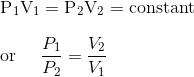
Pressure and volume are direct and opposite ratio with temperature remaining constant, that is pressure is inversely proportional to volume of the gas.
Molarity Formula:
Molarity (M) is defined as the number of moles of solute dissolved in one litre (or one cubic decimetre) of solution,
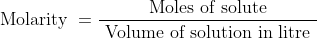
First Law of Thermodynamics:
Heat supplied = Work done by the system + Increase in internal energy
So increase in internal energy = Heat supplied - work done by the system
![\textrm{ie. } \Delta =q+w \ \ \ \ \ \ \ [ \because \textup{ work done by the system is -w}]](https://cache.careers360.mobi/media/articles/uploads/froala_editor/images/2024/11/5/1730807915840.png)
Nernst Equation:
At T = 298K, the Nernst equation is given as follows:
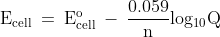 where n is the number of electrons exchanged.
where n is the number of electrons exchanged.
Thus the Nernst equation for the full cell is given as follows:
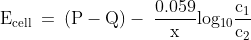
It goes without saying that it is possible to solve any Chemistry question with the help of these basic number schemas rather quickly.
BITSAT 2026 Formulas for Maths
Mathematics in BITSAT is more of calculation than application where time plays a key role. There are several mathematical formulas that can be very helpful in solving maths problems and mastering the following BITSAT Maths formulas will go along way in helping you solve problems much simpler.
Quadratic equation:
A polynomial equation in which the highest degree of a variable term is 2 is called quadratic equation.
Standard form of quadratic equation is ax2 + bx + c = 0
Where a, b and c are constants (they may be real or imaginary) and called the coefficients of the equation and 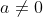 (a is also called the leading coefficient).
(a is also called the leading coefficient).
Eg, -5x2 - 3x + 2 = 0, x2 = 0, (1 + i)x2 - 3x + 2i = 0
As degree of quadratic polynomial is 2, so it always has 2 roots (number of real roots + number of imaginary roots = 2)
The root of the quadratic equation is given by the formula:
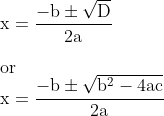
Where D is called the discriminant of the quadratic equation, given by 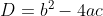 ,
,
Sine Rule
In any
|
Differential equation:
An equation involving independent variable (x), dependent variable (y) and derivative of dependent variable with respect to independent variable
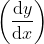
Integration Formulas:
It is inverse process of differentation.
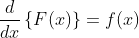
Probability Formula:
P(A)=Number of favorable outcomesTotal number of outcomesP(A) = \frac{\text{Number of favorable outcomes}}{\text{Total number of outcomes}}P(A)=Total number of outcomesNumber of favorable outcomes
Group frequency distribution
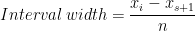
Permutations and Combinations:
Permutation basically means the arrangement of things. And when we talk about arrangement then the order becomes important if the things to be arranged are different from each other (when things to be arranged are the same then order doesn’t have any role to play). So in permutations order of objects becomes important.
Arranging n objects in r places (Same as arranging n objects taken r at a time) is equivalent to filling r places from n things.
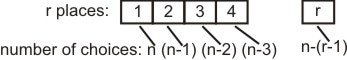
So the number of ways of arranging n objects taken r at a time = n(n - 1) (n - 2) ... (n - r + 1)
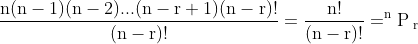
Where 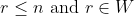
So, the number of ways arranging n different objects taken all at a time = 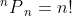 .
.
Area under a Curve:
A=∫abf(x)dxA = \int_a^b f(x) dxA=∫abf(x)dx
Tips to All Students:
In This Guide, You Will Come Across Various Formulas That Will Help You Pass in BITSAT
Daily Practice: It should become a discipline, however, to revise these formulas daily for at least 15-20 minutes, anyway. If you are going to utilize these questions in the test, then the more you drill, the more facile it will be for you to conjure it in your mind.
Create Formula Sheets: Pre Almanac Handout Also need to make the Rubik’s cube template a habanero: Give out a formula sheet according to the person and topic. You may set it aside and keep referring to it for final moment reflection.
Mock Tests: These formulas should be used any time one is handling mock tests. This will help you employ them as effectively in a time-bound manner as it is in a bodily exam such as the BITSAT. For students preparing for BITSAT, you can go with the mocks tests.
Frequently Asked Questions (FAQs)
BITSAT 2026 will be conducted multiple times in two sessions. The first session will be held from April 15–17, 2026, followed by the second session from May 24–26, 2026. Candidates can choose to appear in one or both sessions, with admissions based on the best score obtained across the sessions.
For BITSAT, it is particularly useful to review Physical Chemistry equations from the Ideal Gas Law, through the application of the Arrhenius equation, the Nernst equation, up to the Faraday’s laws of electrolysis. Classes also help in getting the knowledge of some of the major principles concepts of Thermodynamics and Electrochemistry.
For the BITSAT examination, the important formulas in Physics are Newton’s laws of motion, kinematics equations Ohm’s law, Coulomb’s law, work energy formula, magnetic field and lenses formula etc. Closely related important topics repeat during the BITSAT examinations, such as Mechanics, Electrodynamics, and Optics.
Prepare the formula sheet all different for Physics fields, Chemistry fields, and Maths fields. Go through these sheets every day and then try and solve tests and past years question papers appear to be solved using these formulas. Returning to the act of writing them down and solving multiple problems also increases the storage of these items in memory.
In BITSAT which is typically a speed-based exam, you are likely to be faced with 150 questions within 180 minutes only. Maintaining the essential PCM formulas enables to solve concerns, and so, erases the necessity for considering things anew for starters. Understanding these formulas in detail will give you a convenient opportunity to manage time effectively and also improve precision.
Popular Courses and Specializations
List of colleges accepting BITSAT
Browse Engineering Colleges by State
Questions related to BITSAT
On Question asked by student community
Hello aspirant,
BITSAT syllabus for Btech covers physics Chemistry, Mathematics (biology for Pharmacy), English proficiency and logical reasoning. Also includes NCERT syllabus like Testing core concepts in Mechanics, Thermodynamics, Chemical bonding, Calculus and Critical thinking. And also topics include like kinematics, Electrostatics, Organic Chemistry, Algebra, Grammer and Pattern recognition. It
Since you're from Delhi and have already registered for JEE, BITSAT, VITEEE, and CUET, consider these additional exams: SRMJEEE (SRM Institute of Science and Technology), COMEDK UGET (for Karnataka engineering colleges), WBJEE (West Bengal Joint Entrance Examination), AEEE (Amrita Entrance Examination for Amrita Vishwa Vidyapeetham), KIITEE (Kalinga Institute of Industrial
Hello,
For BITSAT 2026, the approximate weightage across subjects is often given as:
Mathematics: ~ 40 %
Physics: ~ 30 %
Chemistry: ~ 25 %
English + Logical Reasoning: ~ 10 % combined
To know the syllabus and questions Check the follwing link,
https://www.careers360.com/exams/bitsat
Kindly check the below link to
Hello,
If you are looking for colleges with good placements other than through JEE or BITSAT, you can consider private and state-level engineering colleges that conduct their own entrance exams or accept board exam scores. Many of these colleges have strong industry connections and placement cells that help students get
Hello Aspirant,
From your BITSAT score of 210, BITS Hyderabad entry supports a very focused choice of integrated M.Sc. (like M.Sc. Physics, Chemistry, Mathematics, Economics or Biology). Generally with this score, admission into the M.Sc. programs at BITS Hyderabad is likely competitive. Based on past trends, the cutoff's for the
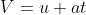
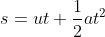
 Displacement
Displacement Initial velocity
Initial velocity acceleration
acceleration time
time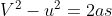
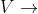 Final Velocity
Final Velocity Displacement
Displacement Initial velocity
Initial velocity acceleration
acceleration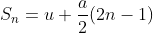
 Initial velocity
Initial velocity uniform acceleration
uniform acceleration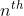 second
second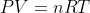
 ABC, the side are proportional to sines of the opposite angle
ABC, the side are proportional to sines of the opposite angle