जेईई मेन्स 2025 जनवरी 23 शिफ्ट 1 तथा शिफ्ट 2 प्रश्न पत्र समाधान सहित: जेईई मेन भारत में इंजीनियरिंग के क्षेत्र में करियर बनाने के इच्छुक छात्रों के लिए एक महत्वपूर्ण परीक्षा है, जो शीर्ष विश्वविद्यालयों में प्रवेश का द्वार है। राष्ट्रीय परीक्षा संस्थान द्वारा जेईई मेन 23 जनवरी शिफ्ट 1 तथा 2 परीक्षा संपन्न हो चुकी है। जेईई मेन परीक्षा शिफ्ट 1 तथा शिफ्ट 2 प्रश्न पत्र तथा उनके समाधान अपडेट किए जा रहे हैं।
जेईई मेन्स 2025 परीक्षा 23 जनवरी शिफ्ट 1 तथा शिफ्ट 2 प्रश्न पत्र और इसके समाधान, उम्मीदवारों को परीक्षा के प्रारूप को समझने, महत्वपूर्ण विषयों की पहचान करने तथा कठिनाई के स्तर का आकलन करने में मदद करेंगे। परीक्षा संरचना में परिवर्तन के साथ, इस वर्ष का पेपर अत्यधिक प्रतिस्पर्धी और चुनौतीपूर्ण होने की उम्मीद है, जो भारत में सबसे महत्वपूर्ण प्रवेश परीक्षाओं में से एक के रूप में अपनी विरासत को जारी रखेगा। जनवरी सत्र के लिए जेईई मेन 2025 परीक्षा 22, 23, 24, 28, 29 और 30 जनवरी को आयोजित की जा रही है। राष्ट्रीय परीक्षा एजेंसी तीन घंटे के लिए जेईई मेन परीक्षा 2025 का आयोजन करेगी।
कुल अवधि | 3 घंटे (180 मिनट) |
कुल प्रश्न | 75 प्रश्न |
अधिकतम अंक | 300 अंक |
परीक्षा का माध्यम | 13 भाषाओं में उपलब्ध |
परीक्षा का तरीका | कंप्यूटर आधारित टेस्ट (सीबीटी) |
प्रश्नों का प्रकार | एमसीक्यू और संख्यात्मक मूल्य आधारित |
इंजीनियरिंग की पढ़ाई करने के इच्छुक भारतीय इंजीनियरों के लिए, जेईई मेन्स एक ज़रूरी परीक्षा है। जेईई मेन्स 2025 परीक्षा 23 जनवरी शिफ्ट 1 प्रश्न पत्र और उसके समाधान जारी होने के बाद, उम्मीदवारों को परीक्षा की चुनौती के स्तर, महत्वपूर्ण विषयों और प्रश्नों के प्रकार के बारे में जानकारी प्रदान करेंगे।
Q.1 Which of the following element doesn't lie on same period
(a) Osmium
(b) Iridium
(c) Palladium
(d) Platinum
Q.2
Which of the following pair of ions are same coloured?
$
\begin{aligned}
& 1 \mathrm{Ti}^{4+}, \mathrm{V}^{3+} \\
& 2 \mathrm{Cr}^{2+}, \mathrm{Cu}^{2+} \\
& 3 \mathrm{Cr}^{3+}, \mathrm{Ni}^{2+} \\
& 4 \mathrm{Mn}^{3+}, \mathrm{Fe}^{2+}
\end{aligned}
$
Q.3 Which of the following react with Hinsberg reagent?
(A) Aniline
(B) $\mathrm{N}, \mathrm{N}$-Dimethyl aniline
(C) Methyl amine
(D) $\mathrm{C}_6 \mathrm{H}_5 \mathrm{NHC}_6 \mathrm{H}_5$
. A only
. A and C only
. $A, C$ and $D$
. A and B only
Q.4
$
\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CH}=0 \xrightarrow[\text { Excess }]{\mathrm{HCHO}}[\mathrm{~A}]
$
Major product $[A]$ will be:
Q.5
Statement 1: Fructose can give tollens test even though it does not have aldehyde group
Statement 2: When reacted with base fructose can undergo rearrangement to produce aldehyde group
(1) If both Statement 1 and Statement 2 are true and the Statement 2 is the correct explanation of the assertion.
(2) If both Statement 1 and Statement 2 are true but Statement $\mathbf{2}$ is not the correct explanation of the assertion.
(3) If Statement 1 is true but Statement 2 is false.
(4) If the Statement 1 and Statement 2 both are false.
Q.6
Q)If for an arithmetic progression, if first term is $\mathbf{3}$ and sum of first four terms is equal to $\frac{1}{5}$ of the sum of next four terms, then the sum of first 20 terms is
(A) 1080
(B) 364
(C) $\mathbf{- 1 0 8 0}$
(D) -364
Q.7
If for the system of linear equations having infinite solutions
$
\begin{aligned}
& (\lambda-4) x+(\lambda-2) y+\lambda z=0 \\
& 2 x+3 y+5 z=0 \\
& x+2 y+6 z=0
\end{aligned}
$
then $\lambda^2+\lambda$ is
Q.8 Find the value of $\sin 70^{\circ}\left(\cot 10^{\circ} \cot 70^{\circ}-1\right)$
Q.9
The displacement of a particle as function of time is $x(t)=A(\sin )+B \cos ^2(t)+c t^2+D$. Find dimension of $\left(\frac{A B C}{D}\right)$
(A) $\mathrm{L}^2$
(B) $\mathrm{L}^{2 \mathrm{~T}} \mathrm{~T}^{-2}$
C $\mathrm{Lt}{ }^{-2}$
(D) $\mathrm{L}^3 \mathrm{~T}$
Q.10.Stat 1: hotter moves faster than cold water.
Stat 2: soap water have higher surface tension than fresh water
Q.11. Value of $\cos ^{-1}\left[\frac{12}{13} \cos x+\frac{5}{13} \sin x\right]$ is
$
\left(x \in\left[\frac{\pi}{2}, \pi\right]\right)
$
$1 \quad x+\tan ^{-1} \frac{12}{13}$
$2 x-\tan ^{-1} \frac{12}{13}$
$3 \quad x-\tan ^{-1} \frac{5}{12}$
$4 \quad x+\tan ^{-1}\left(\frac{4}{5}\right)$
Q.12 If angles of projection for two projectiles are $30^{\circ}$ and $60^{\circ}$ then the ratio of velocities at maximum height is.
Q.13 If $10^{21}$ molecules are removed from $\times \mathrm{mg}$ of $\mathrm{CO}_2(\mathrm{~g})$, then $2.4 \times 10^{-3}$ moles are left. Calculate the value of $x$
Q.14 Area of the larger region bounded by curves $y=|x-1|$ and $x^2+y^2=25$ is
Q.15
If $f(x)$ is continuous at $x=0$, where
$
f(x)=\left\{\begin{array}{cl}
\frac{2}{x}\left(\sin \left(k_1+1\right) x+\sin \left(k_2+1\right) x\right) & x<0 \\
\frac{4}{x} \log \left[\frac{k_2 x+1}{k_1 x+1}\right] & x=0 \\
& x>0
\end{array}\right.
$
Then $k_1^2+k_2^2$ is
Q.16 $q_1=3 \quad S_4=\frac{1}{4}\left(S_8-S_4\right)$ find $S_2=$ ?
Q.17 which of the following Can show face-mer Isomes
a) $\mathrm{Co}\left[(\mathrm{en})_2 \mathrm{Cl}_2\right]$
b) $\left[\mathrm{Co}\left(\mathrm{NH}_3\right)_4 \mathrm{Cl}_2\right]$
c) $\left[\mathrm{Co}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right]_1 \mathrm{X}$
d) $\left[\mathrm{Co}\left(\mathrm{NH}_3\right)_3 \mathrm{Cl}_3\right]$
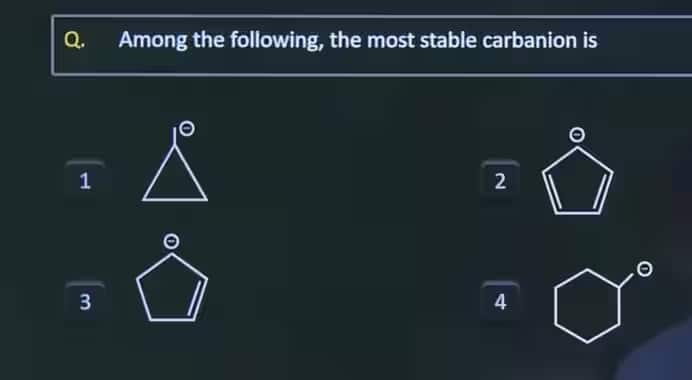
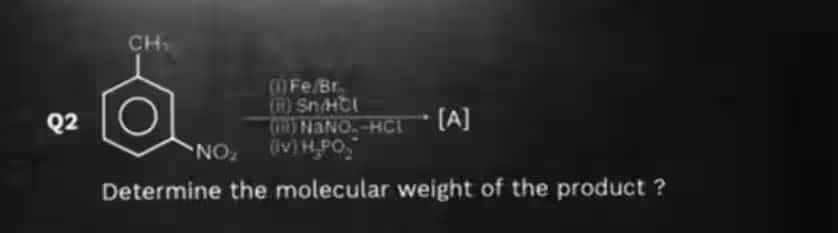
पिछले वर्ष के प्रश्न पत्र जेईई मेन की तैयारी में महत्वपूर्ण भूमिका निभाते हैं। इनका अभ्यास करके, आप परीक्षा पैटर्न और जेईई मेन्स 2025 में आने वाले प्रश्नों के प्रकार को बेहतर ढंग से समझ सकते हैं। पिछले प्रश्नपत्रों की समीक्षा करने से आपको प्रारूप और कठिनाई स्तर से परिचित होने में मदद मिलेगी, जिससे आगामी परीक्षा के लिए आपकी तैयारी बेहतर होगी। मूल्यवान अभ्यास सामग्री के लिए पिछले वर्ष के प्रश्न पत्रों की जांच अवश्य करें।
जेईई मेन 2025 जनवरी 23 शिफ्ट 1 प्रश्न पत्र समाधान के साथ (मेमोरी आधारित प्रश्न)
जेईई मेन 2025 शिफ्ट 2 प्रश्न पत्र समाधान के साथ अब इस पृष्ठ पर उपलब्ध है। हालाँकि, ये संसाधन बाद की शिफ्ट में उपस्थित होने वाले उम्मीदवारों और अप्रैल सत्र की तैयारी करने वालों के लिए महत्वपूर्ण हैं। जेईई मेन्स 23 जनवरी शिफ्ट 2 प्रश्न पत्र को जेईई मेन्स 2025 प्रश्न पत्र पीडीएफ शिफ्ट 2 के साथ संयोजित करना लक्षित तैयारी के लिए आवश्यक है। इससे छात्रों को अप्रैल सत्र के साथ-साथ अन्य शिफ्टों में परीक्षा देने वाले छात्रों की तैयारी में भी मदद मिलेगी।
JEE Main 2025 Shift 2 Question Paper with Solution is now available on this page. However, these resources are crucial for candidates appearing in subsequent shifts and those preparing for the April session. The JEE Mains 23 Jan shift 2 question paper combined with the JEE Mains 2025 question paper pdf shift 2 is essential for targeted preparation. This will help the students to prepare for the April session as well as the ones who have their exams on the other shifts.
Q.1Q. The correct order of melting point of 14 group element is ( $K$ )
$1 \quad \mathrm{C}>\mathrm{Si}>\mathrm{Ge}>\mathrm{Sn}>\mathrm{Pb}$
$2 \quad \mathrm{Si}>\mathrm{C}>\mathrm{Ge}>\mathrm{Sn}>\mathrm{Pb}$
$3 \quad \mathrm{Ge}>\mathrm{Sn}>\mathrm{C}>\mathrm{Si}>\mathrm{Pb}$
$4 \quad \mathrm{C}>\mathrm{Si}>\mathrm{Ge}>\mathrm{Pb}>\mathrm{Sn}$
Q.2What will be effect on pH of water when it is heated
1 Increase
2 Decrease
3 Remains same
$4 \quad \mathrm{pH}$ first increases then decreases
Q.3If a square is divided in $4 \times 4$ squares. If two squares are chosen randomly then the probability that the squares doesn't share common side is
1)$3 / 5$
2)$4 / 5$
3)$3 / 20$
4)$7 / 10$
Q.4If angle of prism $=$ angle of min deviation. Given $\mu=\sqrt{3}$, then angle of prism?
Q.5 $\quad \alpha$-helix protein and $\beta$-pleated sheet protein belong from which of the following structure?
1 Primary
2 Secondary
3 Tertiary
4 Quarternary
Q.6Q: A projective is projected at an angle of Go with horizontal with K.E $\rightarrow$ K.
then find K.E. at $H_{\max }$
Q.7Q1 In $4 \times 4$ board, find probability of choosing two blocks having no same side.
Q.8 There are 5 boys and 4 girls. The sum of number of ways to sit them such that together and number of ways such that no boys sit together is equal to
Q.9 Q. In a series $L C R$ circuit, inductance $L=100 \mathrm{mH}$ and capacitance $C=10 \mathrm{nF}$. The angular frequency of the source when current has maximum amplitude in the circuit is
$1 \quad \frac{10^4}{2 \pi} \mathrm{rad} / \mathrm{s}$
$2 \quad \frac{10^5}{2 \pi} \mathrm{rad} / \mathrm{s}$
$3 \quad 10^5 \mathrm{rad} / \mathrm{s}$
$4 \quad 10^6 \mathrm{rad} / \mathrm{s}$
Q.10Let S be the region consisting of points $(\mathrm{x}, \mathrm{y})$ such that $-1 \leq x \leq 1 \& 0 \leq y \leq a+e^{k \mid x}-e^{-x_1}$ if area bounded by region is $\frac{e^2+8 e+1}{e}$ find " $a$ ".
Q.11The correct order of melting point of 14 group element is $(\mathrm{K})$
(1) $\mathrm{C}>\mathrm{Si}>\mathrm{Ge}>\mathrm{Sn}>\mathrm{Pb}$
(2) $\mathrm{Si}>\mathrm{C}>\mathrm{Ge}>\mathrm{Sn}>\mathrm{Pb}$
(3) $\mathrm{Ge}>\mathrm{Sn}>\mathrm{C}>\mathrm{Si}>\mathrm{Pb}$
(4) $\mathrm{C}>\mathrm{Si}>\mathrm{Ge}>\mathrm{Pb}>\mathrm{Sn}$
Q.12The atomic number of the element with least melting point in group 14?
1)6
2)14
3)50
4)85
Q13A satellite is nine times closer to earth compared to moon. Time period of moon is 27 days then period of satellite is
1)3 days
2)9 days
3)1 days
4)$3 \sqrt{3}$ days
Q.14 Let $f(x)=6+16 \cos \left(\frac{\pi}{3}-x\right) \cos \left(\frac{\pi}{3}+x\right) \cos x \sin 3 x \cos 6 x$ if range of $f(x)$ is $[\alpha, \beta]$ then distance of $(\alpha, \beta)$ from $3 x+4 y+12=0$ is
पिछले वर्षों के प्रश्न पत्रों के लिए नीचे देखें, जो आपको परीक्षा पैटर्न और प्रश्नों का स्पष्ट विचार प्राप्त करने में मदद करेंगे।
23 जनवरी की शिफ्ट पैटर्न के आधार पर जेईई मेन 2025 परीक्षा को पिछली शिफ्ट की तरह मध्यम कठिन कहा जा रहा है। छात्रों को अन्य पालियों के लिए गणित, भौतिकी और रसायन विज्ञान में विभिन्न प्रकार के प्रश्नों की तैयारी करनी चाहिए; यह समझा जा सकता है कि कुछ क्षेत्र दूसरों की तुलना में थोड़े कठिन हो सकते हैं। आइए परीक्षा की संरचना का विश्लेषण करें:
कठिनाई और रुझान विश्लेषण
परीक्षा कुल मिलाकर मध्यम कठिन थी। जबकि रसायन विज्ञान अनुभाग अधिक सुलभ हो सकता है, गणित और भौतिकी के अधिक चुनौतीपूर्ण होने की भविष्यवाणी की गई थी। जेईई मेन्स 2025 प्रश्न पत्र 23 जनवरी शिफ्ट 2 का यह विश्लेषण उच्च स्कोरिंग विषयों को समझने के लिए महत्वपूर्ण है। विशेष रूप से:
गणित: कैलकुलस और बीजगणित पर भार के कारण कठिन, जिसके लिए वैचारिक समझ और अभ्यास की आवश्यकता होती है।
भौतिकी: यांत्रिकी और विद्युत चुंबकत्व पर ध्यान देने के साथ मध्यम रूप से कठिन।
रसायन विज्ञान: आसान, कार्बनिक रसायन विज्ञान पर जोर देने के साथ, यह कई छात्रों के लिए अधिक सरल अनुभाग बनाता है।
यहां जेईई मेन के पिछले वर्ष का विस्तृत विश्लेषण दिया गया है:
कलन:
अवकलन और समाकलन जैसे विषयों पर जोर दिया गया। छात्रों को अधिकतम/न्यूनतम, परिवर्तन की दर और निश्चित समाकलन पर समस्याएं हल करनी थीं।
समाकलन और वक्र के अंतर्गत क्षेत्रफल के अनुप्रयोगों का सामान्यतः परीक्षण किया गया।
बीजगणित:
मूल, अवकलन और गुणधर्मों सहित द्विघात समीकरणों पर अत्यधिक ध्यान केन्द्रित किया गया।
समान्तर श्रेढ़ी (एपी, जीपी, एचपी) का परीक्षण योग सूत्रों और संबंधित अवधारणाओं के उपयोग की आवश्यकता वाली समस्याओं के साथ किया गया।
मैट्रिक्स और निर्धारकों ने भी मैट्रिक्स संचालन और समीकरणों की प्रणालियों को हल करने में उनके अनुप्रयोगों पर प्रश्नों के साथ योगदान दिया। आव्यूह एवं सारणिक ने भी मैट्रिक्स संचालन और समीकरणों की प्रणालियों को हल करने में उनके अनुप्रयोगों पर प्रश्नों के साथ योगदान दिया।
निर्देशांक ज्यामिति:
प्रश्न शंकु वर्गों-वृत्त, दीर्घवृत्त और अतिपरवलय पर केन्द्रित थे। मुख्य समस्याओं में स्पर्शरेखाओं के समीकरण और शंकुओं के गुण शामिल थे।
ज्यामितीय गुणों और समीकरणों से संबंधित प्रश्नों के साथ सीधी रेखाओं और परवलयों का भी परीक्षण किया गया।
वेक्टर और 3D ज्यामिति:
डॉट प्रोडक्ट, क्रॉस प्रोडक्ट, तथा त्रि-आयामी रेखाओं और समतलों के समीकरणों पर प्रश्न शामिल किए गए।
2. भौतिकी अनुभाग
यांत्रिकी:
गति के नियम और कार्य-ऊर्जा की समस्याओं का सबसे अधिक बार परीक्षण किया गया। घर्षण, त्वरण और बल जैसे विषयों को सैद्धांतिक और व्यावहारिक दोनों संदर्भों में शामिल किया गया।
घूर्णी गति में टॉर्क, जड़त्व आघूर्ण और कोणीय संवेग पर प्रश्न थे।
विद्युत चुंबकत्व:
इलेक्ट्रोस्टैटिक्स कूलॉम के नियम, गॉस के नियम और विद्युत क्षेत्रों पर केंद्रित था।
धारा के चुंबकीय प्रभाव में एम्पीयर का नियम, गतिशील आवेशों पर चुंबकीय बल और धाराओं के कारण चुंबकीय क्षेत्र को शामिल किया गया।
विद्युतचुंबकीय प्रेरण में फैराडे के नियम और लेंज़ के नियम पर प्रश्न शामिल थे।
आधुनिक भौतिकी:
प्रकाश विद्युत प्रभाव, बोहर मॉडल और परमाणु भौतिकी पर प्रश्न प्रमुख थे।
पदार्थ की द्वैध प्रकृति और डी ब्रोग्ली की परिकल्पना का परीक्षण करना।
ऊष्मप्रवैगिकी:
विषयों में ऊष्मागतिकी के प्रथम और द्वितीय नियम, एन्ट्रॉपी, ऊष्मा स्थानांतरण और आंतरिक ऊर्जा शामिल थे।
Recognized as Institute of Eminence by Govt. of India | NAAC ‘A++’ Grade | Upto 75% Scholarships | Application Deadline: 15th Jan
100% Placement Record | Highest CTC 54 LPA | NAAC A++ Accredited | Ranked #62 in India by NIRF Ranking 2025 | JEE & JET Scores Accepted
कार्बनिक रसायन विज्ञान (40%):
अभिक्रिया तंत्रों पर आधारित प्रश्नों की प्रधानता, जैसे कि एस.एन.1/एस.एन.2, इलेक्ट्रोफिलिक प्रतिस्थापन, तथा मुक्त मूलक अभिक्रियाएं।
हाइड्रोकार्बन, अल्कोहल और सुगंधित यौगिकों पर विषय अक्सर दिखाई देते थे।
भौतिक रसायन (35%):
ऊष्मागतिकी पर प्रश्नों में एन्थैल्पी, एन्ट्रॉपी और गिब्स मुक्त ऊर्जा शामिल थे।
रासायनिक गतिकी और साम्यावस्था का बड़े पैमाने पर परीक्षण किया गया, जिसमें दर नियमों, ले शातेलिए के सिद्धांत और सक्रियण ऊर्जा पर ध्यान केंद्रित किया गया।
अकार्बनिक रसायन शास्त्र (25%):
संकरण, आणविक कक्षीय सिद्धांत और वीएसईपीआर सिद्धांत सहित रासायनिक बंधन पर ध्यान केंद्रित किया गया।
समन्वय यौगिक के प्रश्नों में लिगैंड, ऑक्सीकरण अवस्थाएं और संकुल शामिल थे।
आयनीकरण ऊर्जा, परमाणु त्रिज्या और विद्युत ऋणात्मकता जैसे आवधिक रुझानों को कवर किया गया।
पिछले वर्षों की तुलना में, जेईई मेन 23 जनवरी शिफ्ट 1 तथा शिफ्ट 2 परीक्षा की संरचना उसी तरह आयोजित होने की उम्मीद है, जिसमें प्रश्नों के वितरण पर प्रमुख जोर दिया जाएगा। गणित में कैलकुलस और बीजगणित पर ध्यान केन्द्रित रहेगा, तथा भौतिकी में यांत्रिकी और विद्युत-चुम्बकत्व पर प्रभुत्व रहेगा। उम्मीद है कि पिछले वर्षों की तरह ऑर्गेनिक केमिस्ट्री भी रसायन विज्ञान में सबसे बड़ा खंड बना रहेगा।
On Question asked by student community
You can get free mock tests for JEE 2026 on the Careers360 website. The mock tests are based on the latest exam pattern and help in understanding the level of questions and time management. You just need to register and start attempting the tests online.
Direct link for JEE mock
Hello,
If you passed 12th in 2025 and did not appear in JEE till now, then this is your eligibility:
JEE Main can be given for 3 consecutive years after 12th.
Each year has 2 sessions .
You are eligible in 2025, 2026 and 2027 .
Since you
Hello,
For JEE (for IT / engineering) :
10th percentage
There is no fixed minimum percentage needed in Class 10 to prepare for JEE.
You just need to pass Class 10 .
Important part is Class 12
You must study Physics, Chemistry, and Mathematics in Class 11 and 12 .
Hello there,
Understanding and solving different question papers is one of the best practices for preparation ,especially when it comes to JEE. It gives you a proper understanding of the exam pattern, important topics to cover, and the marking scheme.
Here is the link attached from the official website of
Hello
You're a student in the medical stream, and you should have studied Physics, Chemistry, Mathematics, and Biology subjects; then you're eligible for the JEE Mains exam, because the eligibility for the JEE Mains exam is that you must have studied Physics, Chemistry, and Mathematics subjects. You should focus heavily
Among top 100 Universities Globally in the Times Higher Education (THE) Interdisciplinary Science Rankings 2026
National level exam conducted by VIT University, Vellore | Ranked #16 by NIRF for Engg. | NAAC A++ Accredited
Recognized as Institute of Eminence by Govt. of India | NAAC ‘A++’ Grade | Upto 75% Scholarships | Application Deadline: 15th Jan
Ranked #43 among Engineering colleges in India by NIRF | Highest Package 1.3 CR , 100% Placements
100% Placement Record | Highest CTC 54 LPA | NAAC A++ Accredited | Ranked #62 in India by NIRF Ranking 2025 | JEE & JET Scores Accepted
NAAC A+ & NBA Accredited | QS I-Gauge Gold rated University | Highest CTC 52 LPA | 300+ Companies | Avail Scholarships Application Deadline: 28th Feb’26
