Yes, during JEE Main registration, you can choose up to four preferred exam cities in order of priority. Since you are staying in Kota but belong to Bihar, you can select both locations. For example, Kota as your first choice and your hometown city in Bihar as another option.
When the admit card is released (usually a week before the exam), the final center will be allotted from your chosen options.
Tricks To Solve JEE Main Maths MCQs Within Seconds
Ongoing Event
JEE Main Application Date:31 Oct' 25 - 27 Nov' 25
We all are familiar with Multiple Choice Questions (MCQs). These are the questions which give us some options, usually 4, out of which one, or sometimes more than one, is correct. The Joint Entrance Examination Main, or JEE Main, has 30 Questions per subject out of which 20 are MCQs with only one correct option. Generally in mathematics for some questions, you will find the options in integer values like chapters trigonometry, sequence and series and others for which you can easily get the answer by using the values given in options directly to solve questions and verify it in less time. In this article, we are going to explain some ticks and trips with the help of examples which you can implement in various questions. Let us understand the trick with the help of some examples.
LiveJEE Main 2026 Registration LIVE: NTA JEE application form at jeemain.nta.nic.in; exam centres, patternNov 2, 2025 | 9:40 PM ISTRead More
The National Testing Agency (NTA) has announced that a standard onscreen calculator will not be provided during the JEE Main 2026 computer-based test. The agency explained that a “typographical error” in the JEE Main 2026 information bulletin had incorrectly mentioned the use of calculators in the exam.
Example 1
If A + B = 45°, then find the value of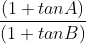 
equals
a)1
b)0
c)2
d)1
Let us first try to understand the question. It means that if A + B = 45°, then the value of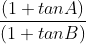 
is always constant, which is equal to one of the options. So, for all combinations of angles A and B whose sum is 45°, the value of (
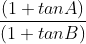will always be the same, which is equal to one of the four options.
So, whether (A = 0° and B = 45°) or (A = 1 ° and B = 44°) or (A = 10° and B = 35°), they all will give the same value of (1+tanA)(1+tanB). So, we can easily replace A and B with some convenient values of angles and get the required value of (1+tanA) * (1+tanB). Let us put A = 0° and B = 45°,
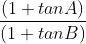= (1+tan0°)(1+tan45°) = (1 + 0)(1 + 1) = 1*2 = 2
So, option C is correct
Example 2
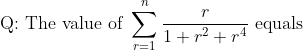
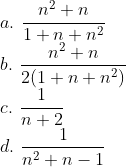
Now we have to select the option that gives the correct sum for all natural number values of n. So, the correct option has to be true for n = 1, 2, 3, …and all other natural number values of n. So, if any option is giving the wrong sum for n = 1, we can be sure that that option is incorrect.
Also Read,
- Science Olympiads: How To Plan For Competitive Exams
- 5 Apps To Help You Avoid Distractions, Become More Productive
- Identifying Signs Of Learning Disability And Getting A Diagnosis
Let us try to find the options that are incorrect.
For n = 1, the actual sum of the given series is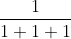 
= 
Checking what value option A for n = 1: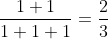 
. So, it gives the wrong answer for n = 1, and hence it cannot give the correct answer for all values of n. Hence this option is wrong.
Checking what value option B for n = 1: (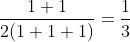
. So, it gives the correct answer for n = 1. But this might give wrong answers for higher values of n. So, we will not mark this as correct right now.
Checking what value option C for n = 1: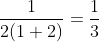 
So, it gives the correct answer for n = 1. But this might give wrong answers for higher values of n. So, we will not mark this as correct right now.
Checking what value option D for n = 1: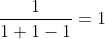 
So, it gives the wrong answer for n = 1, and hence it cannot give the correct answer for all values of n. Hence this option is wrong.
Now both options A and D are eliminated, and one of option B or C is correct. Let us now see which of these two is giving the correct answer for n = 2.
For n = 2, the actual sum of the given series is
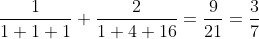
Checking what value option B for n = 2: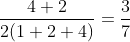 
. So, it gives the correct answer for n = 2 as well. But this might give wrong answers for higher values of n. So, we will not mark this as correct right now.
Checking what value option C for n = 2: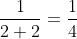 
. So, it gives the wrong answer for n = 2, and hence it cannot give the correct answer for all values of n. Hence this option is wrong.
Now we know that 3 out of 4 options are wrong, and only option B is left. So, we can safely mark option B as correct.
Example 3
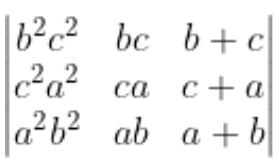
If the value of the determinant given equals ka3b3c3, then the value of k is
a)1
b)0
c)-1
d)2
This question means that the value of the determinant always equals ka3b3c3 for all sets of values of a, b and c. In such questions, we can substitute some values of a, b and c and check to see the values of the determinant and the value of ka3b3c3. Also try to keep values of a, b and c such that ka3b3c3 does not become 0. So we will keep non-zero values of a, b and c. Let us put a = b = c = 1.
The value of the determinant is
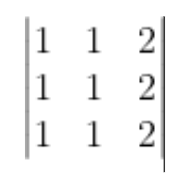
which equals 0 (As two columns are the same) and the value of ka3b3c3 is k. So comparing these, we get k = 0.
Know when to use this trick and when not to. Don't use it for questions with more than one right answer or for multiple-choice questions where 'None of these' or 'All of these' is the only correct option.
Articles
Related Stories
|
Upcoming Engineering Exams
Certifications By Top Providers
Explore Top Universities Across Globe
Popular Courses and Specializations
List of colleges accepting JEE Main
Browse Engineering Colleges by State
Questions related to JEE Main
On Question asked by student community
Have a question related to JEE Main ?
Hello,
Hope you understand.
Hello Devanshi
To know the Cutoff of the JEE Mains exam paper for the year 2025, and for previous year, you can visit the link I am attaching below. The link will provide you with the data and help you to improve your performance.
https://engineering.careers360.com/articles/jee-main-cutoff-for-b-arch-b-planning
Hello dear candidate,
Here is the link of NIPER JEE previous year questions along with their solutions, it has question papers with solutions for year 2019-2025, including your requirement of 2021 :-
https://pharmacy.careers360.com/download/ebooks/niper-jee-previous-year-question-paper-pdf
I hope you find this helpful. Thank you.
Hello dear candidate,
You can fill your JEE main and advance forms 2026 normally . No, your 11th registration number will not cause any problem.
You will be treated as 12th appearing student in 2026, not as a dropper . You just need to make sure that your CBSE 12th result comes out in 2026 before counselling.
Thank you.
To be eligible for Himachal Pradesh state quota you must have passed atleast two examinations from Himachal pradesh including the 10th and 12th grades. The other criteria are for government employee wards, if the parents have worked there for atleast two years and completed their 10th and 12th from HP.
Study Resources, Applications and Opportunities
Recognized as Institute of Eminence by Govt. of India | NAAC ‘A++’ Grade | Upto 75% Scholarships
UPES B.Tech Admissions 2026
ApplyRanked #43 among Engineering colleges in India by NIRF | Highest Package 1.3 CR , 100% Placements
Lovely Professional University B.Tech Admissions 2026
ApplyIndia's Largest University | NAAC A++ | 100% Placements Record | Highest CTC 2.5 Cr PA | 150 + Programmes across Multiple Disciplines
New Horizon College of Engineering B.E. Admissions 2025
ApplyAICTE ‘Platinum’ institute | NIRF 2024 Rank Band 151-200 under the engineering category | Tier-1 accreditation by NBA | Merit & Sports Scholarships
IITs- A Complete Guide
Get nowDive into everything you need to know about IITs—from eligibility and cutoffs to fees and placements.
Atlas SkillTech University | B.Tech Admissions
ApplyHands on Mentoring and Code Coaching | Cutting Edge Curriculum with Real World Application
JEE Main Notifications
Explore Career Options
By IndustryNever miss an JEE Main update
Get timely JEE Main updates directly to your inbox. Stay informed!