Orthogonal matrix and Unitary matrix and Idempotent matrix - Practice Questions & MCQ

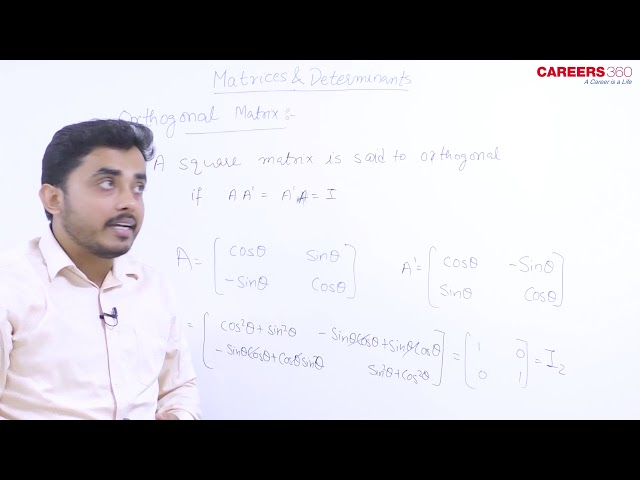
Orthogonal matrix
A square matrix is said to be an orthogonal matrix if $A A^{\prime}=I$, where $I$ is the identity matrix.

Note
1. $A A^{\prime}=I \Rightarrow A^{-1}=A$
2. If $A$ and $B$ are orthogonal then $A B$ is also orthogonal.
3. If $A$ is orthogonal the $A^{-1}$ and $A^{\prime}$ is also orthogonal.

Unitary matrix
Let $A$ is a square matrix, and if $A A^?=I$, where $I$ is the identity matrix, then $A$ is said to be a unitary matrix.
Note:
1. If $A A^{\text {? }}=1$, then $A^{-1}=A^{\text {? }}$
2. If $A$ and $B$ are unitary, Then $A B$ is also unitary.
3. If $A$ is unitary, then $A^{-1}$ and $A^{\prime}$ are also unitary.

Idempotent matrix
A square matrix is said to be an idempotent matrix if it satisfies the condition $A^2=A$.