EASYAmity University Noida-B.Tech Admissions 2026
Among top 100 Universities Globally in the Times Higher Education (THE) Interdisciplinary Science Rankings 2026
Search Colleges, Exams, Schools & more
Login
Motion Of Connected Blocks Over Pulley - Practice Questions & MCQ
Edited By admin | Updated on Sep 18, 2023 18:34 AM | #JEE Main
Quick Facts
-
Motion of connected blocks over pulley is considered one the most difficult concept.
-
46 Questions around this concept.
Solve by difficulty
Two masses m1 = 5kg and m2 = 4.8 kg tied to a string are hanging over a light frictionless pulley. What is the acceleration (in m/s2 ) of the masses when lifted free to move?
( g = 9.8 m/s2 )
A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 ( vertically) . If the acceleration of the system is g/8, then the ratio of the masses is
Two masses of 10 kg and 9 kg are connected by a string that passes over a smooth pulley; What is the tension in the string $\left(g=9.81 \mathrm{~ms}^{-2}\right)$
JEE Main 2026 Session 2 Memory Based Questions: All Shift (April 2, 4, 5, 6 & 8)
JEE Main 2026: Rank Predictor | College Predictor | YouTube Live Analysis - April 8 Shift 2
Comprehensive Guide: IIT's | NIT's | IIIT's
Don't Miss: Foreign Universities in India | India's Best B.Tech Counsellors in your city - Book Your Seat
Three masses each of 4 kg are connected by a string that passes through a smooth pulley; Tension between mass b and c?
Direction : In the following question , a statement of Assertion (A) is followed by a statement of reason (R) . Mark the correct choice as:
Assertion : The tension force on a body always act away from the body.
Reason : Tension force are always pushing force.
Two blocks of masses 5kg and 10kg are connected to a pulley as shown in fig. What will be the acceleration if the pulley is set free?
What is the mechanical advantage of a single fixed pulley?
The system shown is released at rest. Speed of block A (in m/s), after B has descended by 2 cm is
As shown in the figure, a block of mass m = 200 g is suspended by a string. A force F is applied slowly at the lower end of the string.What will be the maximum value of F if bearing strength of the string is 5N?
JEE Main 2026 Rank Predictor
Use the JEE Main 2026 Rank Predictor to estimate your expected rank based on your scores or percentile and plan your college options smartly.
Try NowA monkey of mass ${ }^{\prime} m$ ' is climbing a rope hanging from the roof with acceleration ${ }^{\prime} a^{\prime}$. The coefficient of static friction between the body of the monkey and the rope is $\mu$. The value of friction force on the monkey and tension in the string are respectively.
Concepts Covered - 2
Motion of connected blocks over pulley
Equation of motion for $m_1$
$
F_{n e t}=T-m_1 g=m_1 a
$
Equation of Motion for $m_2$
$
\begin{aligned}
& F_{\text {net }}=m_2 g-T=m_2 a \\
& a=\frac{\left[m_2-m_1\right] g}{m_1+m_2} \\
& T=\frac{2 m_1 m_2 g}{m_1+m_2}
\end{aligned}
$
When one Block is hanging from a rope and one on the table
-
When one Block is hanging, other is on the Table
$\begin{aligned} a & =\frac{m_2 g}{m_1+m_2} \\ T & =\frac{m_1 m_2 g}{m_1+m_2}\end{aligned}$
-
Three blocks, two are hanging and one is at the rest on the smooth horizontal table
$
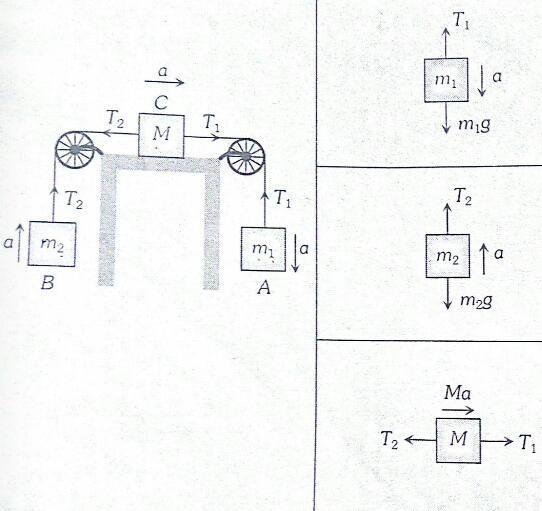
\begin{aligned}
& m_1 a=m_1 g-T_1 \\
& m_2 a=T_2-m_2 g \\
& T_1-T_2=M a
\end{aligned}
$
$
\begin{aligned}
& a=\frac{\left(m_1-m_2\right) g}{m_1+m_2+M} \\
& T_1=\frac{m_1\left(2 m_2+M\right) g}{\left(m_1+m_2+M\right)} \\
& T_2=\frac{m_2\left(2 m_1+M\right) g}{\left(m_1+m_2+M\right)}
\end{aligned}
$
Study it with Videos
"Stay in the loop. Receive exam news, study resources, and expert advice!"
Get Answer to all your questions
B.Tech/B.Arch Admissions OPEN
Amity University Noida-B.Tech Admissions 2026
ApplyAmong top 100 Universities Globally in the Times Higher Education (THE) Interdisciplinary Science Rankings 2026
RV University, Mysuru | B.Tech Admissions 2026
ApplyWorld-class and highly qualified engineering faculty. High-quality global education at an affordable cost
Amrita University B.Tech 2026
ApplyApplication Deadline: 15th April | Recognized as Institute of Eminence by Govt. of India | NAAC ‘A++’ Grade | Upto 75% Scholarships
VIT Bhopal University | B.Arch Admissions 2026
ApplyMark presence in the Modern Architectural field with Bachelor of Architecture | Highest CTC : 70 LPA | Accepts NATA Score
Somaiya Vidyavihar University B.Tech Admissions 2026
ApplyHighest CTC 58 LPA | Avg CTC 11.35 LPA| 150+ Recruiters
Shoolini University Admissions 2026
ApplyNAAC A+ Grade | Ranked 503 Globally (QS World University Rankings 2026)