Maximum Length Of Hung Chain - Practice Questions & MCQ
Edited By admin | Updated on Sep 18, 2023 18:34 AM | #JEE Main
Quick Facts
-
6 Questions around this concept.
Solve by difficulty
MEDIUMA heavy uniform chain lies on a horizontal table top. If the coefficient of friction between the chain and the table surface is 0.25, then the maximum fraction of the length of the chain that can hang over one edge of the table is
Length of chain is $L$ and coefficient of static friction is $\mu$. Calculate the maximum length of the chain which can be hung from the table without sliding. Maximum length of hung chain
A uniform rope of length I lies on a table. If the coefficient of friction is $\mu$ then the maximum length $x$ of the part of this rope which can overhang from the edge of the table without sliding down is
New: JEE Main 2026 Registration Link | Top 30 Most Repeated Questions
JEE Main Prep: Study Plan | Preparation Tips | High Scoring Chapters and Topics
JEE Main QP & Mock: Previous 10 Year Questions | Chapter Wise PYQs | Mock test Series
JEE Main Most Scoring Concept: January 2025 Session | April 2025 Session
The length of the chain is 1 m and the coefficient of static friction is $\mu$. Calculate the maximum length of chain which can be hung from the table without sliding $(\mu=0.5)$
A uniform rope of total length $l$ is at rest on a table with fraction $f$ of its length hanging (see figure). If the coefficient of friction between the table and the chain is $\mu$ then
Concepts Covered - 1
Maximum Length of Hung Chain
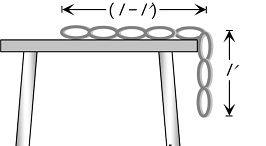
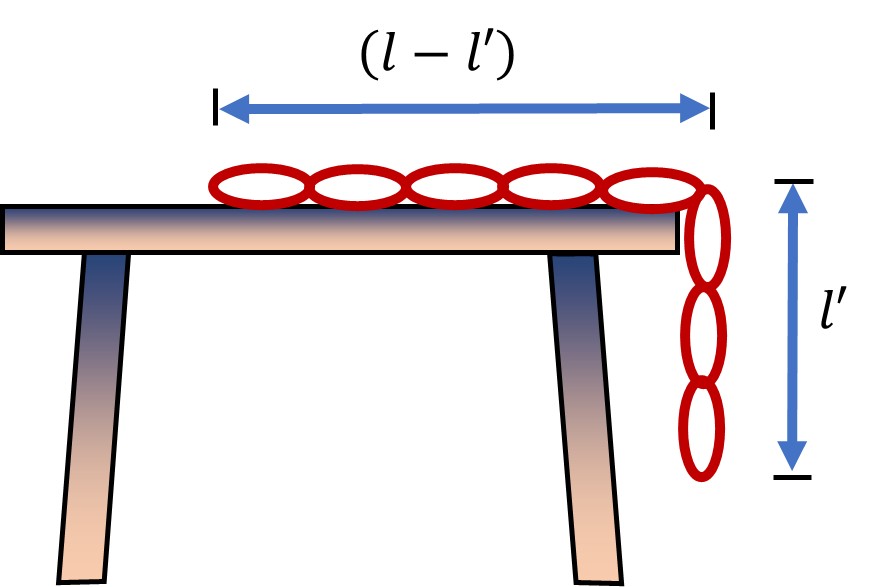
A uniform chain of length l is placed on the table in such a manner that its l' part is hanging over the edge of the table without sliding.
$
\mu=\frac{m_2}{m_1}=\frac{\text { mass hanging from table }}{\text { mass on table }}
$
The chain will have uniform linear density.
So the ratio of mass and ratio of length for any part of the chain will be equal.
$
\begin{aligned}
& \mu=\frac{\text { length of part hanging from table }}{\text { length of part on table }}=\frac{l^{\prime}}{l-l^{\prime}} \\
& l^{\prime}=\frac{\mu l}{(\mu+1)}
\end{aligned}
$
Where $l=$ length of chain
$l^{\prime}=$ chain hanging
$
\left(l-l^{\prime}\right)=\text { chain lying on table }
$
Study it with Videos
Maximum Length of Hung Chain"Stay in the loop. Receive exam news, study resources, and expert advice!"
Get Answer to all your questions
Study Resources, Applications and Opportunities
Recognized as Institute of Eminence by Govt. of India | NAAC ‘A++’ Grade | Upto 75% Scholarships
UPES B.Tech Admissions 2026
ApplyRanked #43 among Engineering colleges in India by NIRF | Highest Package 1.3 CR , 100% Placements
Lovely Professional University B.Tech Admissions 2026
ApplyIndia's Largest University | NAAC A++ | 100% Placements Record | Highest CTC 2.5 Cr PA | 150 + Programmes across Multiple Disciplines
New Horizon College of Engineering B.E. Admissions 2025
ApplyAICTE ‘Platinum’ institute | NIRF 2024 Rank Band 151-200 under the engineering category | Tier-1 accreditation by NBA | Merit & Sports Scholarships
IITs- A Complete Guide
Get nowDive into everything you need to know about IITs—from eligibility and cutoffs to fees and placements.
Atlas SkillTech University | B.Tech Admissions
ApplyHands on Mentoring and Code Coaching | Cutting Edge Curriculum with Real World Application