Calculation Of Necessary Force In Different Conditions On Rough Surface - Practice Questions & MCQ

• Case 1:- Minimum pulling force P at an angle α from the horizontal

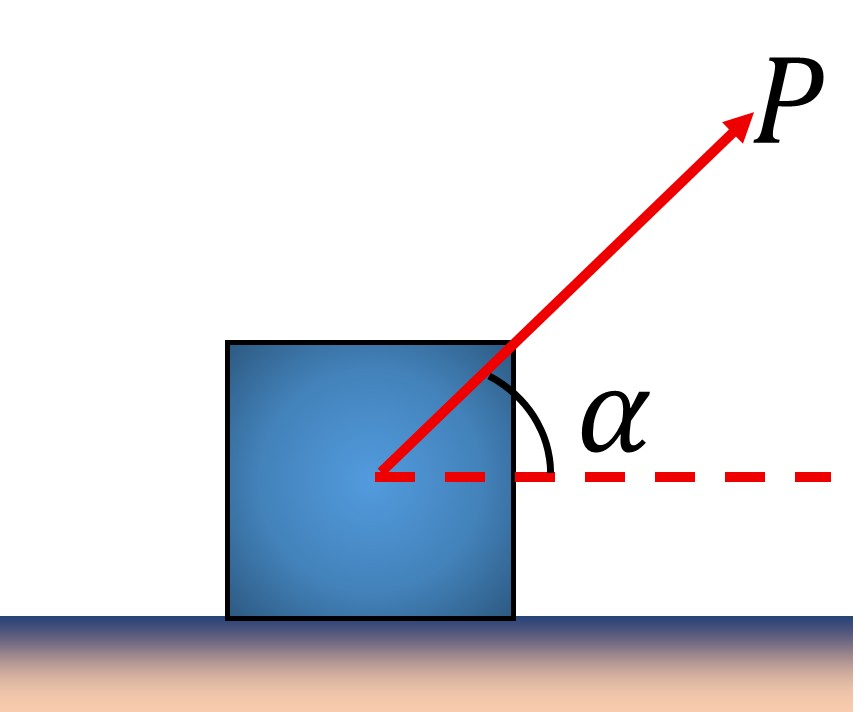
By resolving P in the horizontal and vertical direction, we get:

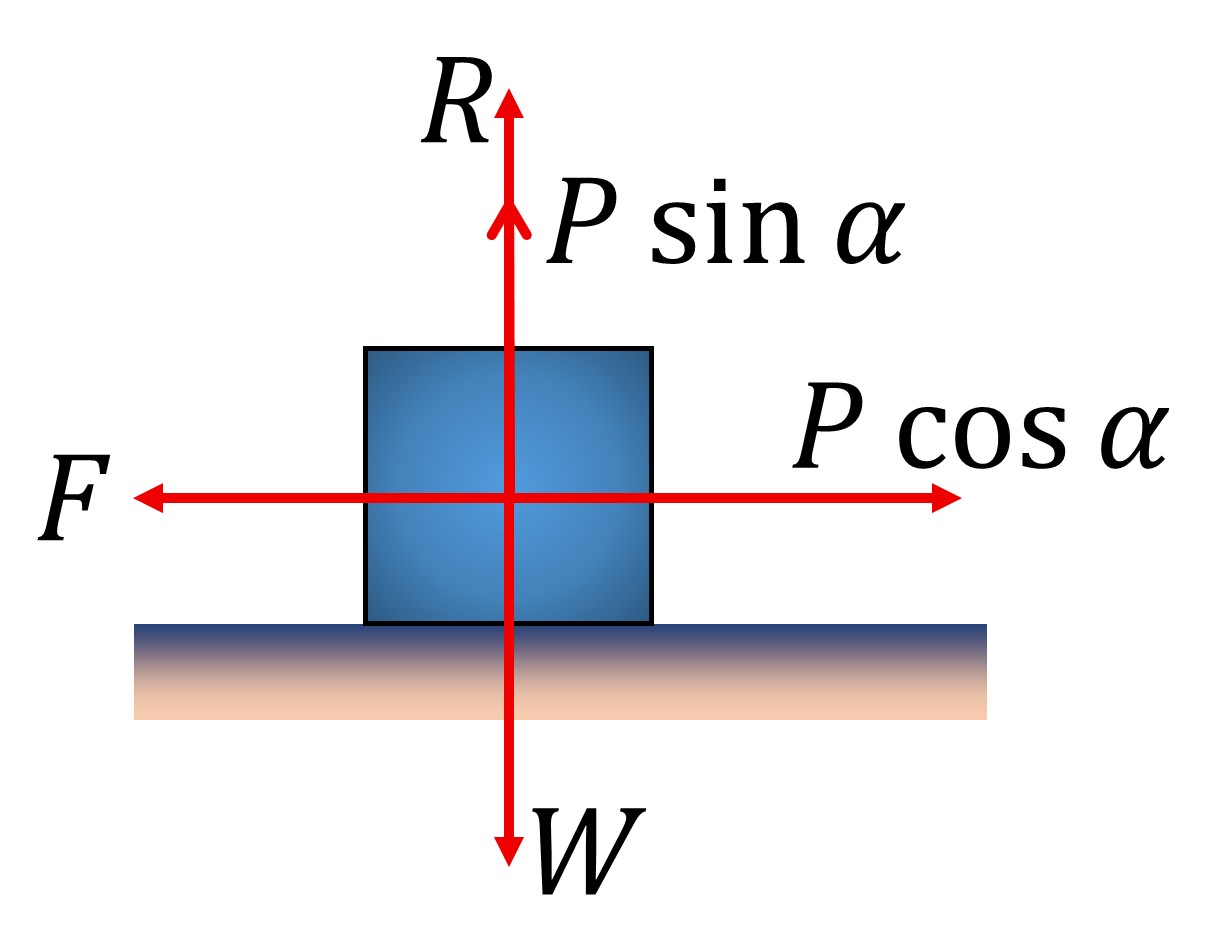
where F is the friction force.

For the condition of equilibrium,

$
\begin{aligned}
& F=P \cos \alpha \\
& R=W-P \sin \alpha
\end{aligned}
$

By substituting these values in $F=\mu R$, we get:

$
\begin{aligned}
& P \cos \alpha=\mu(W-P \sin \alpha) \\
& U s e=\mu=\tan \theta \\
& \Rightarrow P \cos \alpha=\frac{\sin \theta}{\cos \theta}(W-P \sin \alpha) \\
& P=\frac{W \sin \theta}{\cos (\alpha-\theta)}
\end{aligned}
$
 

    where P is the pulling force,

R is a normal reaction

W is the weight

• Case 2:- Minimum pushing force P at an angle α from the horizontal

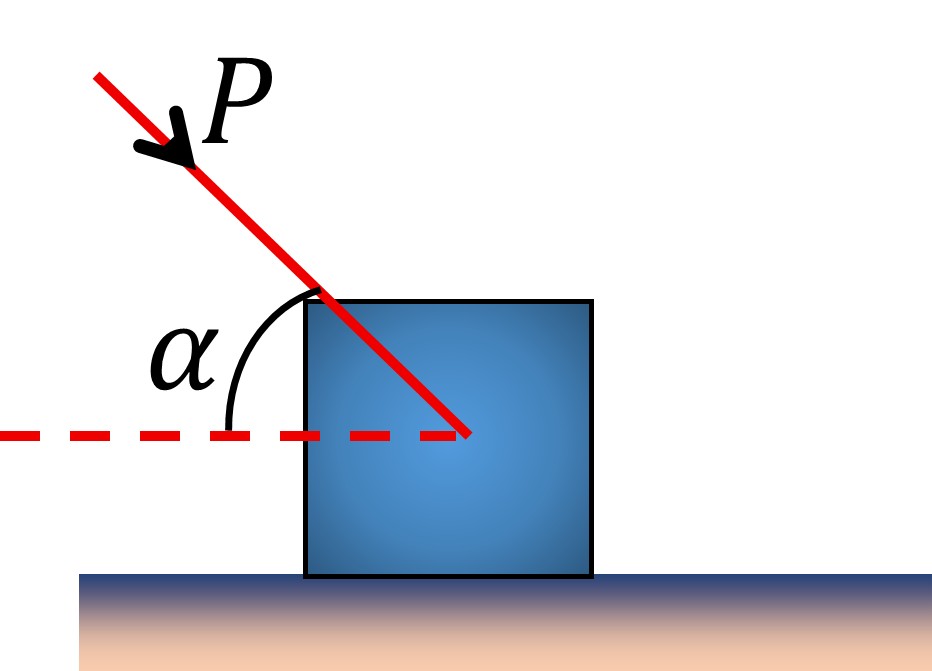
By resolving P in the horizontal and vertical direction, we get:

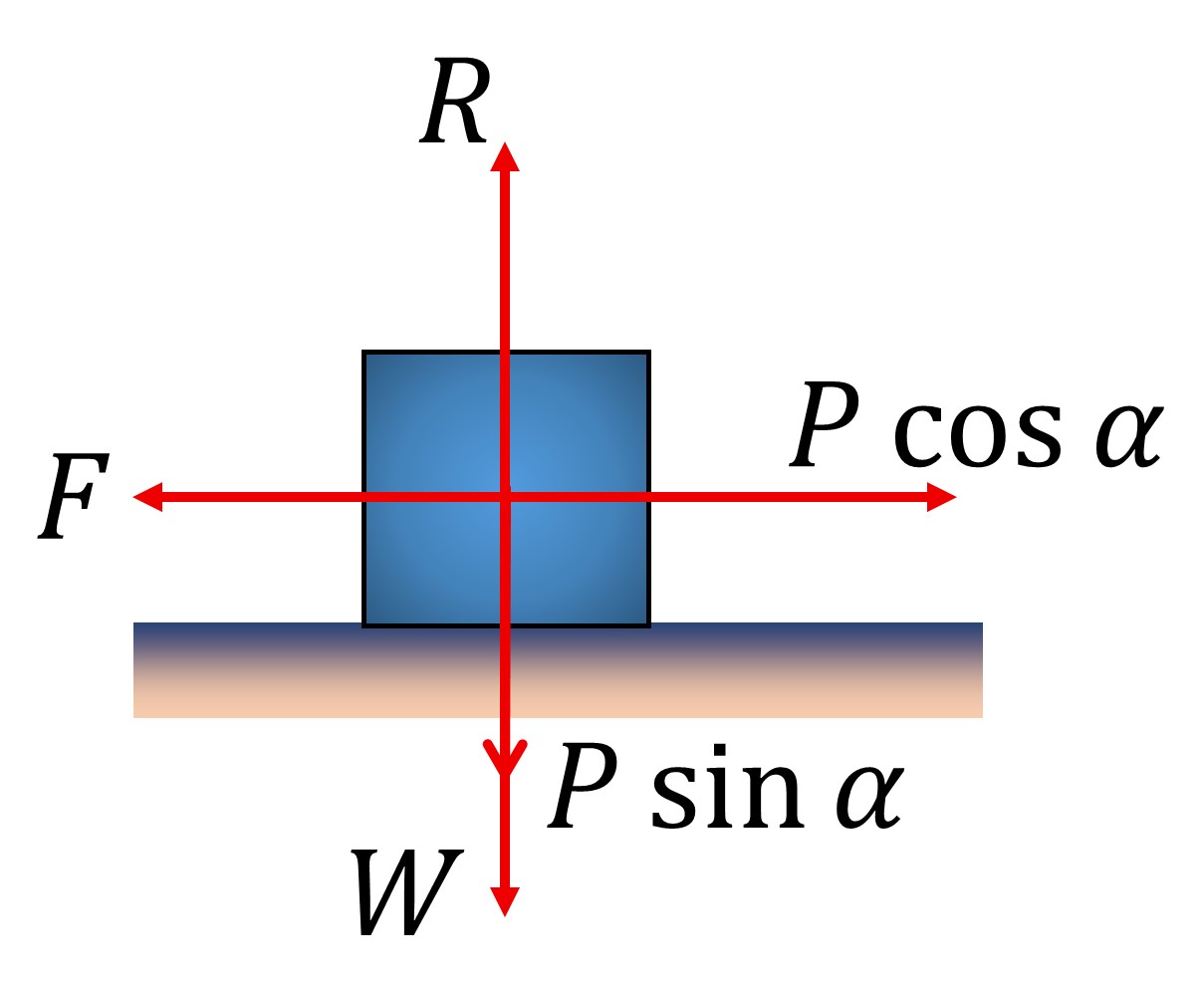
      For the condition of equilibrium,

$
\begin{aligned}
& F=P \cos \alpha \\
& R=W+P \sin \alpha
\end{aligned}
$

By substituting these values in $F=\mu R$, we get:

$
\begin{aligned}
& P \cos \alpha=\mu(W+P \sin \alpha) \\
& U s e=\mu=\tan \theta \\
& \Rightarrow P \cos \alpha=\frac{\sin \theta}{\cos \theta}(W+P \sin \alpha) \\
& P=\frac{W \sin \theta}{\cos (\alpha+\theta)}
\end{aligned}
$
 

• Case 3:- Minimum pulling force P to move the body upwards on an inclined plane

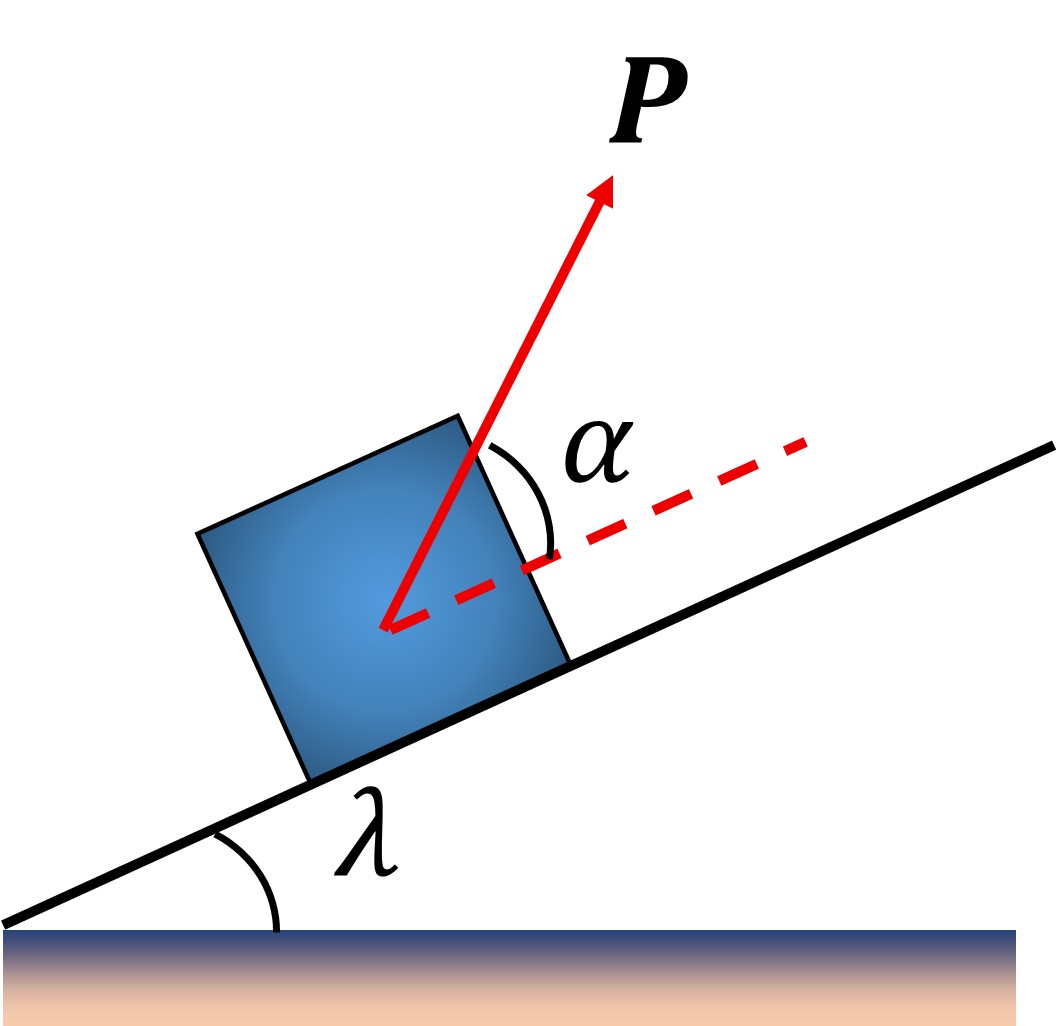
          By resolving P in the direction of the plane and perpendicular to the plane, we get:

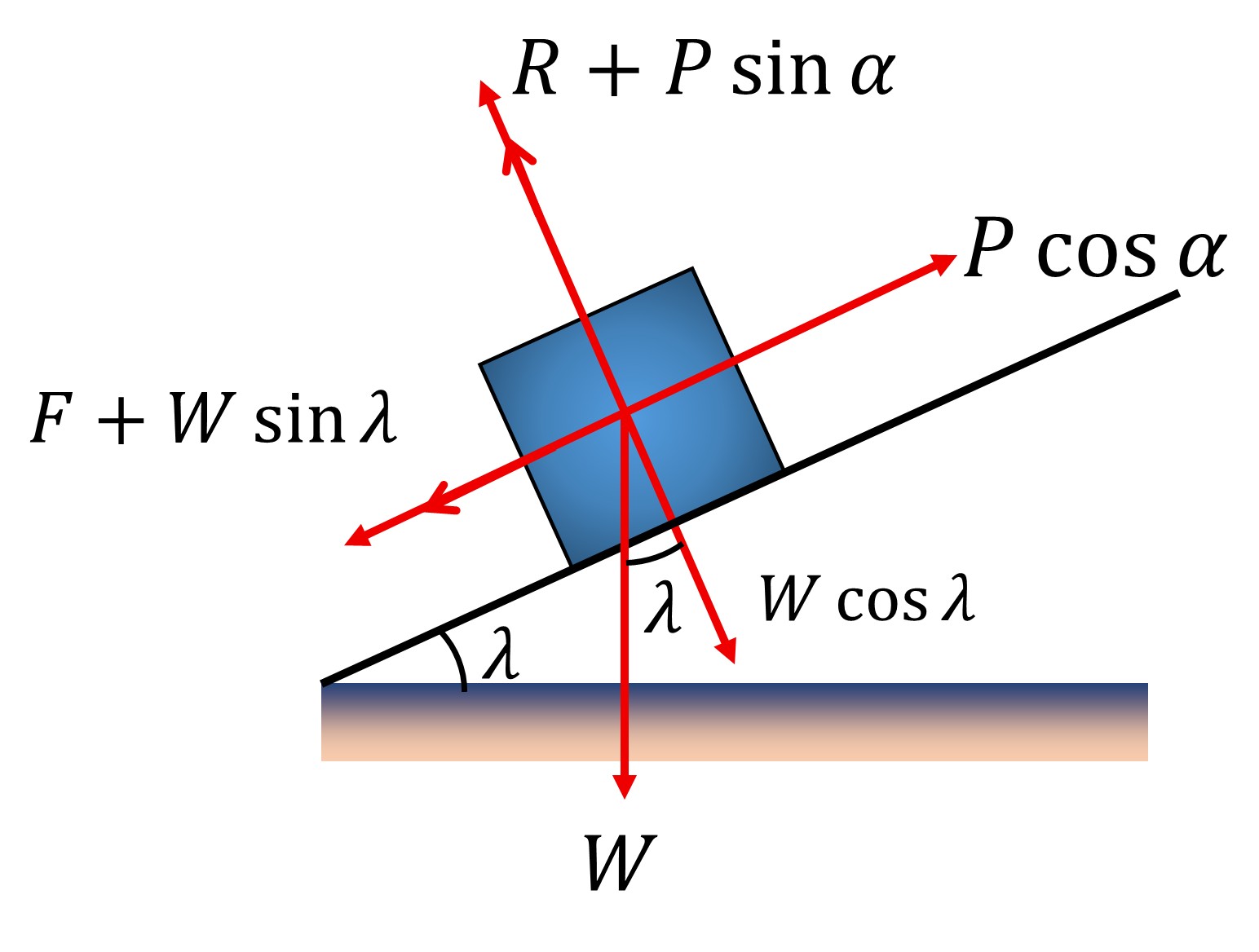
                     For the condition of equilibrium

$
\begin{aligned}
& R+P \sin \alpha=W \cos \lambda \Rightarrow R=W \cos \lambda-P \sin \alpha \\
& F+W \sin \lambda=P \cos \alpha \Rightarrow F=P \cos \alpha-W \sin \lambda
\end{aligned}
$

By substituting these values in $F=\mu R$, we get:

$
P=\frac{W \sin (\theta+\lambda)}{\cos (\alpha-\theta)}
$

Where $\theta$ is the angle of friction such that, $\mu=\tan \theta$

• Case 4:- Minimum force to move a body in a downward direction along the surface of the inclined plane

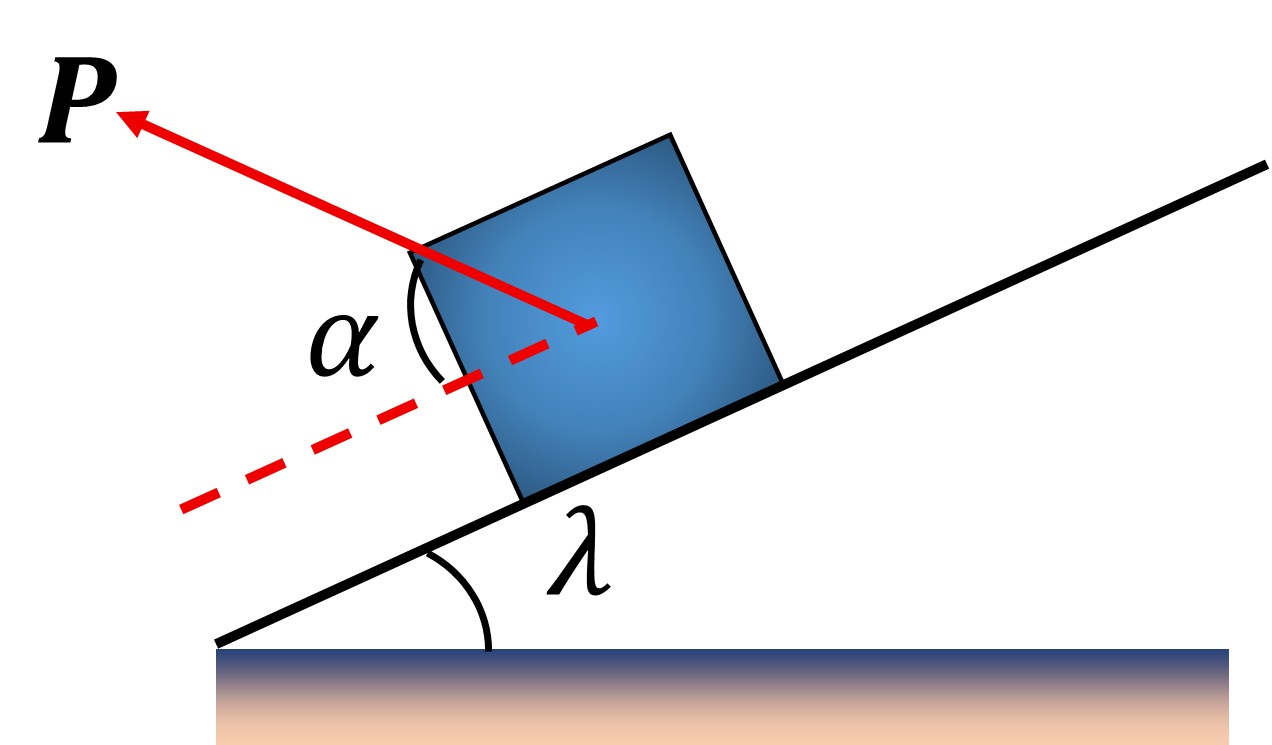
         By resolving P in the direction of the plane and perpendicular to the plane, we get:

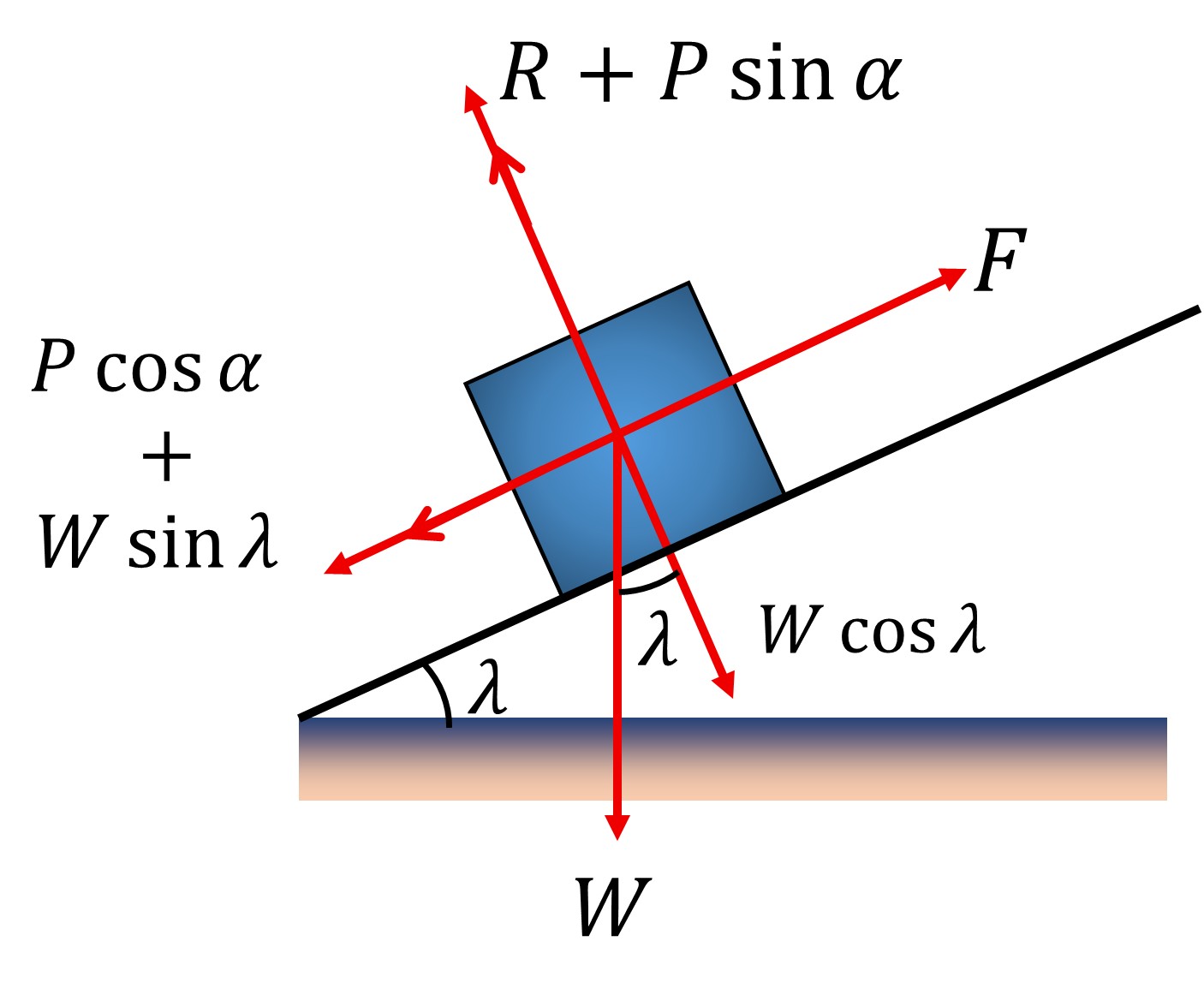
         For the condition of equilibrium,

$
\begin{aligned}
& R+P \sin \alpha=W \cos \lambda \Rightarrow R=W \cos \lambda-P \sin \alpha \\
& F=P \cos \alpha+W \sin \lambda
\end{aligned}
$

By substituting these values in $F=\mu R$, we get:

$
P=\frac{W \sin (\theta-\lambda)}{\cos (\alpha-\theta)}
$

Where $\theta$ is the angle of friction such that, $\mu=\tan \theta$

• Case 5:- Minimum force to avoid sliding of a body down on an inclined plane    

As the block has tendency to slip downward, friction force will act up the incline. For the minimum value of P, the friction force is limiting and the block is in equilibrium.

         Free Body Diagram of the block-

For the condition of equilibrium-

$
\begin{aligned}
& \mathrm{R}+\mathrm{P} \sin \alpha=\mathrm{mg} \cos \lambda \\
& \Rightarrow \mathrm{R}=\mathrm{mg} \cos \lambda-\mathrm{P} \sin \alpha \\
& \text { Limiting friction }- \\
& \mathrm{f}_{\mathrm{l}}=\mu \mathrm{R} \\
& \Rightarrow f_l=\mu(m g \cos \lambda-P \sin \alpha) \ldots \ldots(1) \\
& f_l=m g \sin \lambda-P \cos \alpha \ldots(2) \\
& \text { From equation (1) and (2)- } \\
& m g \sin \lambda-P \cos \alpha=\mu(m g \cos \lambda-P \sin \alpha) \\
& \theta \rightarrow \operatorname{angle} \text { of friction } \\
& \mu=\tan \theta \\
& \mathrm{P}(\cos \alpha-\tan \theta \sin \alpha)=\mathrm{mg}(\sin \lambda-\tan \theta \cos \lambda) \\
& \Rightarrow P=\frac{m g \sin (\theta-\lambda)}{\cos (\theta+\alpha)}
\end{aligned}
$
 

• Case 6:- Minimum Force of Motion along the horizontal surface and its direction

Let the force P be applied at an angle α with the horizontal.

Let the friction force on the block be F.

F.B.D of the block-

                  For vertical equilibrium,

$
\begin{aligned}
& \mathrm{R}+\mathrm{P} \sin \alpha=\mathrm{mg} \\
& \Rightarrow \therefore \mathrm{R}=\mathrm{mg}-\mathrm{Psin} \alpha
\end{aligned}
$

and for horizontal motion,

$
\mathrm{P} \cos \alpha \geq \mathrm{F} \Rightarrow \mathrm{P} \cos \alpha \geq \mu \mathrm{R}
$

Substituting the value of $R$, we get:-

$
\begin{aligned}
\mathrm{P} \cos \alpha & \geq \mu(\mathrm{mg}-\mathrm{P} \sin \alpha) \\
\Rightarrow \mathrm{P} & \geq \frac{\mu \mathrm{mg}}{\cos \alpha+\mu \sin \alpha}
\end{aligned}
$

For the force P to be minimum $(\cos \alpha+\mu \sin \alpha)$ must be maximum i.e.,

$
\begin{aligned}
& \frac{\mathrm{d}}{\mathrm{~d} \alpha}[\cos \alpha+\mu \sin \alpha]=0 \\
& \Rightarrow-\sin \alpha+\mu \cos \alpha=0 \\
& \therefore \tan \alpha=\mu \\
& \Rightarrow \alpha=\tan ^{-1}(\mu)=\text { angle of friction. }
\end{aligned}
$

i.e. For the minimum value of $P$, its angle from the horizontal should be equal to the angle of friction.
$\mathrm{As} \tan \alpha=\mu$, so from the figure,

$
\sin \alpha=\frac{\mu}{\sqrt{1+\mu^2}} \quad \operatorname{and} \quad \cos \alpha=\frac{1}{\sqrt{1+\mu^2}}
$

By substituting these values,

$
\begin{aligned}
\mathrm{P} & \geq \frac{\mu \mathrm{mg}}{\frac{1}{\sqrt{1+\mu^2}}+\frac{\mu^2}{\sqrt{1+\mu^2}}} \\
& \Rightarrow \mathrm{P} \geq \frac{\mu \mathrm{mg}}{\sqrt{1+\mu^2}} \\
& \therefore \mathrm{P}_{\min }=\frac{\mu \mathrm{mg}}{\sqrt{1+\mu^2}}
\end{aligned}
$