EASYVIT - VITEEE 2025
ApplyNational level exam conducted by VIT University, Vellore | Ranked #11 by NIRF for Engg. | NAAC A++ Accredited | Last Date to Apply: 31st March | NO Further Extensions!
Banking Of Road - Practice Questions & MCQ
Edited By admin | Updated on Sep 18, 2023 18:34 AM | #JEE Main
Quick Facts
-
Banking of Road is considered one the most difficult concept.
-
12 Questions around this concept.
Solve by difficulty
A train is moving with a speed of $12 \mathrm{~m} / \mathrm{s}$ on rails which are $1.5 \mathrm{~m}$ apart. To negotiate a curve of radius $400 \mathrm{~m}$, the height by which the outer rail should be raised with respect to the inner rail is (Given, $g=10 \mathrm{~m} / \mathrm{s}^2$ )
A car of $800 \mathrm{~kg}$ is taking turn on a banked road of radius $300 \mathrm{~m}$ and angle of banking $30^{\circ}$. If the coefficient of static friction is 0.2 then the maximum speed with which the car can negotiate the turn safely: $\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2, \sqrt{3}=1.73\right)$
A car of mass m is moving on a concave bridge of radius r with velocity v as shown in the diagram for what value of the reaction on the car by the bridge will be maximum.
Where $\theta$ is the angle made by a vertical line
JEE Main 2025: City Slip Link | Study Plan | Official Question Paper (Session 1)
JEE Main 2025: Sample Papers | Mock Tests | PYQs | High Scoring Topics | College Predictor
New: Meet Careers360 experts in your city and get guidance on shortlisting colleges
Apply to TOP B.Tech /BE Entrance exams: VITEEE | MET | AEEE | BITSAT
Concepts Covered - 1
Banking of Road
-
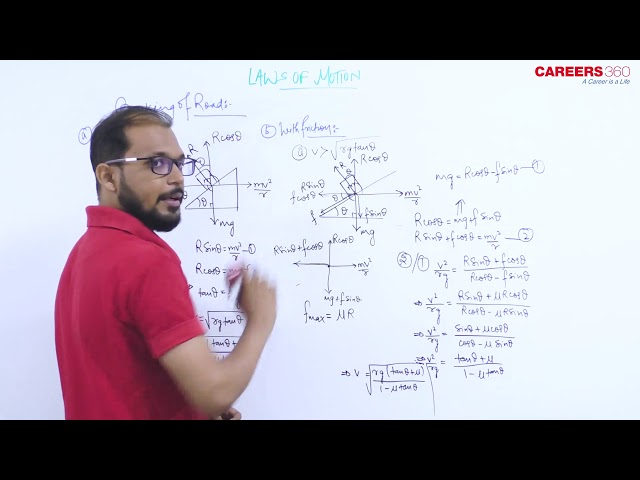
Without friction
From figure
$
\begin{aligned}
& R \cos \theta=m g \\
& R \sin \theta=\frac{m v^2}{r} \\
& \tan \theta=\frac{v^2}{r g} \\
& \tan \theta=\frac{\omega^2 r}{g}=\frac{V \omega}{g}=\frac{h}{l} \\
& \mathrm{~h}=\text { height of outer edge from the ground level } \\
& l=\text { width of the road } \\
& \mathrm{r}=\text { radius }
\end{aligned}
$
-
If friction is also present
$
\frac{V^2}{r g}=\frac{\mu+\tan \theta}{1-\mu \tan \theta}
$
Where $\theta=$ angle of banking
$\mu=$ coefficient of friction
$V=$ velocity
Maximum speed on a banked frictional road
$
V=\sqrt{\frac{r g(\mu+\tan \theta)}{1-\mu \tan \theta}}
$
Study it with Videos
Banking of Road"Stay in the loop. Receive exam news, study resources, and expert advice!"
Get Answer to all your questions
JEE Main Articles
Back to top