Variation Of Pressure - Practice Questions & MCQ

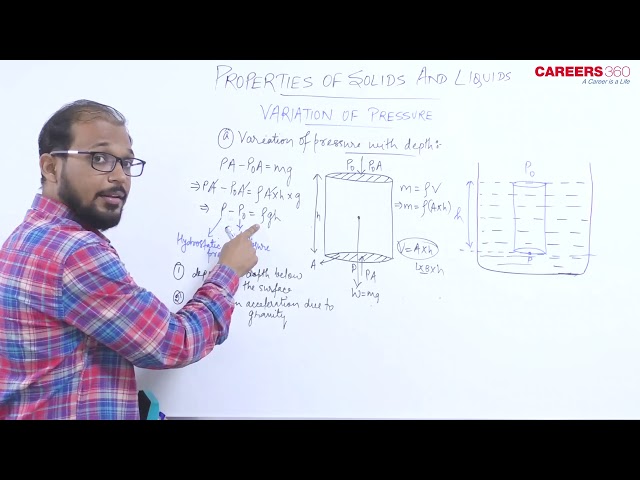
1. Variation of pressure with depth

• Pressure varies with height/depth

       Have a look at the below figure

Here P₀= Atmospheric pressure at the upper surface

And   h= depth below the  upper surface 

$\rho=$ density of liquid
$\mathrm{P}=$ Hydrostatic pressure for a point at depth h below the upper surface
Then P is given by $P=P_0+\rho g h$
Means Pressure increases with depth linearly.
- $\quad$ Hydrostatic pressure $=$ Absolute $\operatorname{Pressure}=P=P_0+\rho g h$

Absolute Pressure is always positive, It can never be zero.
From equation $P=P_0+\rho g h$

We can say that 

1. Hydrostatic pressure depends on 

• h=depth of the point below the surface

• $\rho$=nature of liquid

• g=acceleration due to gravity

2. Hydrostatic pressure does not  depend on 

• amount of liquid 

• the shape of the container

      From this, we can say that for the below figure where the liquid is filled in vessels of different shapes to the same height,

the pressure at the base in each vessel will be the same, though

the volume or weight of the liquid in different vessels will be different.

I.e In the above figure $P_A=P_B=P_C$
- Gauge Pressure- Gauge Pressure is known as the pressure difference between hydrostatic and atmospheric pressure.

So Gauge Pressure is given as $P-P_0=$ gauge pressure

In the equation

$$
P=P_0+\rho g h
$$

The term $\rho g h$ is known as pressure due to liquid column of height $h$
We can rewrite the above equation as $\rho g h=P-P_0$
Or we can say that Gauge Pressure $=\rho g h=P-P_0$
It may be positive or negative or zero

2. Variation of pressure along Horizontally

The pressure is uniform on a horizontal line.

For the below figure

        In horizontal line or in horizontal plane in stationary liquid

        $P_A=P_B=P_C$