EASYVIT - VITEEE 2025
National level exam conducted by VIT University, Vellore | Ranked #11 by NIRF for Engg. | NAAC A++ Accredited | Last Date to Apply: 31st March | NO Further Extensions!
Hooke’s Law - Practice Questions & MCQ
Edited By admin | Updated on Sep 18, 2023 18:34 AM | #JEE Main
Quick Facts
-
Hooke’s law is considered one of the most asked concept.
-
134 Questions around this concept.
Solve by difficulty
A wire elongates by $l \mathrm{~mm}$ when a load $W$ is hanged from it. If the wire goes over a pulley and two weights $W$ each are hung at the two ends, the elongation of the wire will be (in mm )
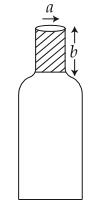
A bottle has an opening of radius a and length b. A cork of length b and radius (a + a) where (a<<a) is compressed to fit into the opening completely (See figure). If the bulk modulus of cork is B and frictional coefficient between the bottle and cork is µ then the force needed to push the cork into the bottle is :
A thin steel ring of inner radius r and cross-section area A to be mounted on a wheel of radius $R(R>r)$. If the Young modulus of the metal ring is Y then the tension in the steel ring is
JEE Main 2025: Admit Card Link | Study Plan | Official Question Paper (Session 1)
JEE Main 2025: Sample Papers | Mock Tests | PYQs | High Scoring Topics | College Predictor
New: Meet Careers360 experts in your city and get guidance on shortlisting colleges
Apply to TOP B.Tech /BE Entrance exams: VITEEE | MET | AEEE | BITSAT
A rod, of length $L$ at room temperature and uniform area of cross-section $A$, is made of a metal having a coefficient of linear expansion $\alpha /{ }^{\circ} \mathrm{C}$. It is observed that an external compressive force F, is applied on each of its ends, and prevents any change in the length of the rod when its temperature rises by $\Delta T K$. Young's modulus, Y, for this metal, is:
The maximum stretching force of humans is $81 \times 10^4 \mathrm{~V}$, However the Young's modulus for stretch is $36 \times 10^9 \mathrm{~Pa}$. Then what is longitudinal strain $\left(\frac{\Delta_l}{l}=?\right) \longrightarrow \quad\left(A=9 \mathrm{~cm}^2\right)$
According to Hooke's law of elasticity if stress is increased the ratio of stress to strain
The unit of Young's modulus of elasticity is-
An object of mass 'm' is suspended at the end of a mass-less wire of length L and area of cross-section A. Young's modulus of the maternal of the wire is Y. if the mass is pulled down slightly its freq. of oscillation along the vertical direction is :
There is no change in the volume of a wire due to a change in its length on stretching. The Poisson's ratio of the material of the wire is
JEE Main 2025 - 10 Full Mock Test
Aspirants who are preparing for JEE Main can download JEE Main 2025 mock test pdf which includes 10 full mock test, high scoring chapters and topics according to latest pattern and syllabus.
Download EBookConsider two cylindrical rods of identical dimensions, one of rubber and the other of steel. Both the rods are fixed rigidly at one end of the roof. A mass M is attached to each of the free ends at the centre of the rods. Then:
Concepts Covered - 1
Hooke’s law
Hooke’s law states that if the deformation is small, the stress in a body is proportional to the corresponding strain, i.e.,
$
\begin{gathered}
\text { Stress } \propto \text { Strain } \\
\Rightarrow \text { Stress }=E(\text { Strain }) \\
\Rightarrow E=\frac{\text { Stress }}{\text { Strain }}
\end{gathered}
$
Where E is called as Modulus of elasticity and it depends on the nature of the material and temperature of the body and is independent of the dimensions of the body.
Unit of Modulus of elasticity $=\mathrm{N} / \mathrm{m}^2$
- Modulus of elasticity is of three types:-
a. Young's Modulus(Y):- It is defined as the ratio of longitudinal stress to longitudinal strain.
$
Y=\frac{\text { longitudinal stress }}{\text { longitudinal strain }}=\frac{F / A}{\Delta L / L}=\frac{F l}{A \Delta L}
$
b. Shear Modulus or Modulus of rigidity(G):- It is defined as the ratio of shearing stress to the shearing strain.
$
G=\frac{\text { shearing stress }}{\text { shearing strain }}=\frac{F / A}{x / L}=\frac{F l}{A x}=\frac{F}{A \phi}
$
c. Bulk Modulus(B):- It is defined as the ratio of volume stress to the volume strain.
$
\begin{gathered}
\text { Volumestress }=\frac{F}{A}=\text { Pressure } \\
B=-\frac{P}{\Delta V / V}
\end{gathered}
$
where $\mathrm{P}=$ increase in pressure, $\mathrm{V}=$ original volume, $\Delta V=$ change in volume
The negative sign indicates that with the increase in pressure, volume decreases by $\Delta V$.
- Compressibility(C):- The reciprocal of bulk modulus is called as compressibility.
$
C=\frac{1}{B}=-\frac{\Delta V / V}{P}
$
- Unit of compressibility:- N-1m2
- Poisson's ratio:- The ratio of lateral strain to longitudinal strain is called Poisson’s ratio (
).
- Lateral strain : The ratio of change in radius or diameter to the original radius or diameter is called lateral strain.
- Longitudinal strain : The ratio of change in length to the original length is called longitudinal strain.
$\sigma=-\frac{\Delta d / d}{\Delta l / l}$
where negative sign is due to decrease in the transverse length
Study it with Videos
Hooke’s law"Stay in the loop. Receive exam news, study resources, and expert advice!"
Books
Reference Books
Clear your Basics with NCERT
E-books & Sample Papers
Get Answer to all your questions
JEE Main Articles
Mar 30, 2025
Back to top