Relation Between Volumetric Strain, Lateral Strain And Poisson’s Ratio - Practice Questions & MCQ
Quick Facts
-
20 Questions around this concept.
Solve by difficulty
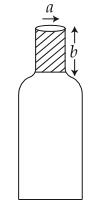
A bottle has an opening of radius a and length b. A cork of length b and radius (a + a) where (a<<a) is compressed to fit into the opening completely (See figure). If the bulk modulus of cork is B and frictional coefficient between the bottle and cork is µ then the force needed to push the cork into the bottle is :
The ratio of change in volume to the original volume is defined as -
A rod of metal 10 cm at $20^{\circ} \mathrm{C} \quad \alpha$ of rod is $11 \times 10^{-6} /{ }^{\circ} \mathrm{c}$ at $19^{\circ} \mathrm{c}$ it will be
New: JEE Main 2026 City Intimation Slip Link
JEE Main Sample Papers: Physics | Chemistry | Maths | Top 30 Repeated Questions
JEE Main QP & Mock: Previous 10 Year Questions | Chapter Wise PYQs | Mock test Series
Concepts Covered - 1

Let us long rod have a length L and radius ' r ', then volume of this $\operatorname{rod}=\pi r^2 L$. $\qquad$
Now, Differentiating both the sides of $(1)$, we get
$
d V=\pi r^2 d L+\pi 2 r L d r
$
Now, dividing both the sides by volume of rod, i.e., $\pi r^2 L$, we get,
$
\frac{d V}{V}=\frac{\pi r^2 d L}{\pi r^2 L}+\frac{\pi 2 r L d r}{\pi r^2 L}=\frac{d L}{L}+2 \frac{d r}{r} \ldots(2)
$
So we can say that,
Volumetric strain = Longitudinal strain + 2(Lateral strain)
Also, equation(2) can be written as,
$
\begin{array}{r}
\Rightarrow \frac{d V}{V}=\frac{d L}{L}-2 \sigma \frac{d L}{L}=(1-2 \sigma) \frac{d L}{L} \\
\text { This is because, }\left[\sigma=\frac{-d r / r}{d L / L} \Rightarrow \frac{d r}{r}=-\sigma \frac{d L}{L}\right]
\end{array}
$
Special case -
- When $\sigma=0.5$, then $d V=0$. It means that the substance is incompressible, so there is no change in volume.
- If a material having $\sigma=0$, it means lateral strain is zero. So, when a substance is stretched its length increases without any decrease in diameter. For example - cork has $\sigma=0$. Also, in this case change in volume is maximum.
Study it with Videos
"Stay in the loop. Receive exam news, study resources, and expert advice!"













