Sticking Of A Block With Accelerated Cart - Practice Questions & MCQ

While solving with the help of the concept of pseudo force.

When a cart moves with some acceleration toward right then a pseudo force (ma) acts on block toward left.

This force (ma) is an action force by a block on the cart. 

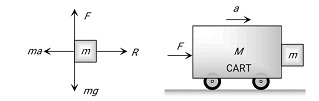
Now block will remain static w.r.t.cart. If friction force= μR≥mg

For equilibrium condition

$
\begin{aligned}
& \mu m a \geq m g \\
& a \geq \frac{g}{\mu}
\end{aligned}
$

$
\begin{aligned}
& \mathrm{R}=\mathrm{ma} \\
& \therefore \quad a_{\min }=\frac{g}{\mu}
\end{aligned}
$

SO minimum force applied on the cart so that block will remain static w.r.t.cart.

$
F_{\min }=(M+m) \frac{g}{\mu}
$

where
$F_{\text {min }}=$ Minimum force
$a_{\text {min }}=$ minimum acceleration cart
$\mathrm{M}, \mathrm{m}$ are masses of the cart and block respectively