Minimum Mass Hung From The String To Just Start The Motion - Practice Questions & MCQ

 Here m₁ is connected to one end of the string and m₂ is connected to another end of the string. And mass m₂ hung from the string connected by the pulley,

Case 1:-

When a mass m₁ placed on a rough horizontal plane

So  the tension (T) produced in the string will try to start the motion of mass m₁:

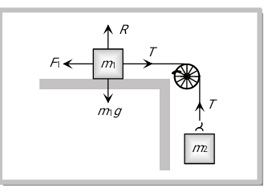
For liming condition

$\begin{aligned} & T=F_l \\ & m_2 g=\mu R \\ & m_2 g=\mu m_1 g \\ & m_2=\mu m_{1=\text { minimum value of } m_2 \text { to start the motion }} \\ & \qquad \begin{array}{l}\mu=\frac{m_2}{m_1} \\ \text { So }\end{array} \\ & \text { where } \mathrm{T}=\text { Tension in a string } \\ & F_l=\text { Limiting friction } \\ & \mu=\text { Coefficient of friction }\end{aligned}$

• Case 2:-

      When a mass m₁ placed on a rough inclined plane 

     So the tension (T) produced in the string will try to start the motion of mass m₁:

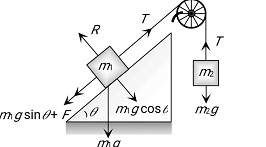
For limiting condition
For $\mathrm{m}_2 \quad T=m_2 g$
For $\mathrm{m}_1 \quad T=m_1 g \sin \theta+F$

$$
T=m_1 g \sin \theta+\mu m_1 \cos \theta
$$

Use (i) \& (ii)
$m_2=m_1[\sin \theta+\mu \cos \theta]=$ minimum value of $m_2$ to start the motion
where $T=$ tension
$\mathrm{m}_2 \mathrm{~g}=$ weigh of mass $\mathrm{m}_2$
$\mathrm{F}=$ limiting friction
Here $\mu=\left[\frac{m_2}{m_1 \cos \theta}-\tan \theta\right]$
$\mu={ }_{\text {coefficient of friction }}$