Law of Sines - Practice Questions & MCQ

Basic relation b/w sides and angle of the triangle and Sine Rule

In this chapter, we will be using some standard symbols

 In ΔABC, the angles are denoted by capital letters A, B and C and the length of the sides opposite to these angles are denoted by small letters a, b and c respectively.

Angles: $\angle B A C=A, \angle A B C=B, \angle B C A=C$
Sides: $A B=c, A C=b$, and $B C=a$
Semi-perimeter of the $\triangle A B C$, is

$
s=\frac{a+b+c}{2}
$

and it is denoted by s. So, perimeter of $\triangle A B C$ is $2 \mathrm{~s}=\mathrm{a}+\mathrm{b}+\mathrm{c}$.

For any $\triangle A B C$,
$\mathrm{A}+\mathrm{B}+\mathrm{C}=180^{\circ}$
$a+b>c, b+c>a$ and $c+a>b$
$a>0, b>0, c>0$

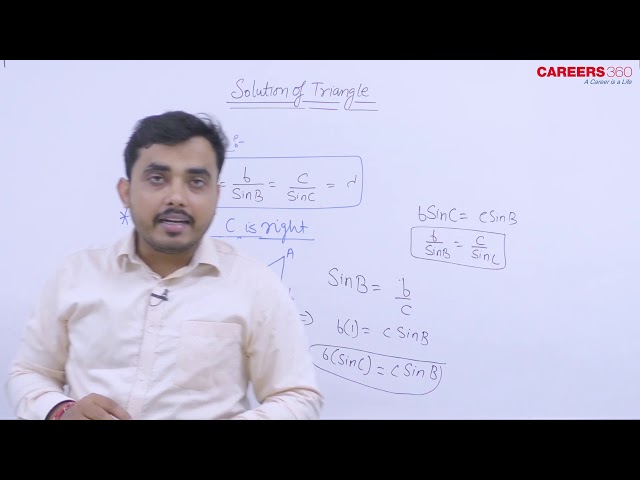
Sine Rule

The ratio of the sine of one of the angles to the length of its opposite side will be equal to the other two ratios of the sine of the angle measure to the opposite side.

$\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}$

Proof:
Using the right triangle relationships, we know that.

$
\sin \mathrm{A}=\frac{\mathrm{h}}{\mathrm{~b}} \text { and } \sin \mathrm{B}=\frac{\mathrm{h}}{\mathrm{a}}
$
Solving both equations for h gives two different expressions for h

$
\mathrm{h}=\mathrm{b} \sin \mathrm{~A} \text { and } \mathrm{h}=\mathrm{a} \sin \mathrm{~B}
$
We then set the expressions equal to each other.

$
\begin{aligned}
b \sin A & =a \sin B \\
\left(\frac{1}{a b}\right)(b \sin A) & =(a \sin B)\left(\frac{1}{a b}\right) \quad \text { Multiply both sides by } \frac{1}{a b} \\
\frac{\sin A}{a} & =\frac{\sin B}{b}
\end{aligned}
$
Similarly, we can compare the other ratios.

$
\frac{\sin A}{a}=\frac{\sin C}{c} \text { and } \frac{\sin B}{b}=\frac{\sin C}{c}
$
Collectively,

$
\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}
$