Coefficient Of Friction Between A Body And Wedge MCQ

Solve by difficulty

The figure shows a horizontal force $\vec{F}$ acting on a block of mass ' $M$ ' on an inclined plane. What is the normal reaction of the block?

$m g \sin θ + F \cos θ$

$m g \sin θ - F \cos θ$

$m g \cos θ - F \sin θ$

$m g \cos θ + F \sin θ$

View Solution

A block rests on a rough inclined plane making an angle of 30^o with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10 N, the mass of the block (in kg) is

(take g = 10 m/s² )

2.0

4.0

1.6

2.5

View Solution

Concepts Covered - 1

Coefficient of Friction Between a Body and Wedge

If the same wedge is made rough then the time taken by it to come down becomes n times more (nt)

Then find the Coefficient of Friction between body and wedge in term of n?

For this make 2 cases

Case 1- A body slides on a smooth wedge of angle θ and its time of descent is t.

Case 2- If the same wedge made rough then the time taken by it to come down becomes n times more (i.e., nt)

(The length of the path in both cases are the same)

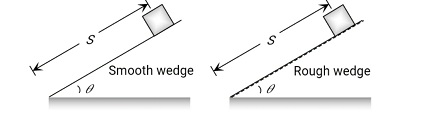
For smooth wedge

$\begin{aligned} S = u \cdot t + \frac{1}{2} a t^{2} \\ S = \frac{1}{2} (g \sin θ) t^{2} \\ u = 0 \\ a = g \sin θ \end{aligned}$

For Rough wedge

$S = \frac{1}{2} g [\sin θ - μ \cos θ] (n t)^{2}$

(i) $=$ (ii)

$μ = \tan θ [1 - \frac{1}{n^{2}}]$

$μ = coefficient of friction$
$θ =$ Angle of inclination
$n =$ an integer

Amity University Noida B.Tech Admissions 2025

Apply

Among Top 30 National Universities for Engineering (NIRF 2024) | 30+ Specializations | AI Powered Learning & State-of-the-Art Facilities

Graphic Era (Deemed to be University) Admissions 2025

Apply

NAAC A+ Grade | Among top 100 universities of India (NIRF 2024) | 40 crore+ scholarships distributed

DA-IICT B.Tech Admissions 2025

Apply

⁠Highest CTC - 82 LPA | Average CTC - 18.25 LPA | NAAC Grade A+ Accredited

UPES B.Tech Admissions 2025

Apply

Ranked #42 among Engineering colleges in India by NIRF | Highest Package 1.3 CR , 100% Placements | Last Date to Apply: 23rd June

Geeta University B.Tech Admissions 2025

Apply

70+ Programs | 40 LPA-Highest Package Offered | Up to 100% Scholarship worth 24 Crore

Chandigarh University Admissions 2025

Apply

Ranked #1 Among all Private Indian Universities in QS Asia Rankings 2025 | Scholarships worth 210 CR

Exams

Colleges

Predictors

Resources

Exams

Colleges & Courses

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors & E-Books

Resources

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

Top Courses & Careers

Colleges

Exams

Colleges

Resources

Quick Links

Exams

Colleges

Resources

Exams

Colleges

Resources

Diploma Colleges

Exams

Resources

Upcoming Events

Other Exams

Exams

Top Schools

Products & Resources

NCERT Study Material

Exams

Colleges

Top Countries

Resources

Exams

Colleges

Upcoming Events

Resources

Engineering Preparation

Medical Preparation

Law Preparation

MBA Preparation

Top Streams

Specializations

Resources

Top Providers

Coefficient Of Friction Between A Body And Wedge - Practice Questions & MCQ

Quick Facts

Solve by difficulty

Concepts Covered - 1

Study it with Videos

Study other Related Concepts

Coefficient Of Friction Between A Body And Wedge Current Topic

Get Answer to all your questions

JEE Main Articles

B.Tech/B.Arch Admissions OPEN

Amity University Noida B.Tech Admissions 2025

Graphic Era (Deemed to be University) Admissions 2025

DA-IICT B.Tech Admissions 2025

UPES B.Tech Admissions 2025

Geeta University B.Tech Admissions 2025

Chandigarh University Admissions 2025

Explore on Careers360

JEE Main