Rigid Bodies: Translational Motion And Rotational Motion - Practice Questions & MCQ

1. Pure Translational motion-

If each particle of it has the same velocity/acceleration at a particular instant of time then A body is said to have pure translational motion.

• Slipping-

It is a motion in which the body slides on a surface without rotation.

Example- Motion of a wheel on a frictionless surface.

Here  friction between the body and surface =f= 0 

Wheel possess only translatory kinetic energy

i.e., $-K_T=\frac{1}{2} m v^2$

2. Pure rotational motion-

When a body rotates such that its axis of rotation does not move then that body is said to have pure rotational motion.

In pure rotational motion, each particle of the body has the same angular velocity/acceleration about its axis of rotation at a particular instant of time.

Example- Spinning  of the wheel about a fixed axis

Here axis of rotation of a wheel is fixed.

Here body possesses only rotatory kinetic energy.

$
\text { I.e } K_R=\frac{1}{2} I \omega^2
$

Here Rotational angular momentum $=\vec{L}=I \vec{w}$
Where $I=$ Moment of inertia about a fixed axis of rotation
$\omega=$ angular velocity of rotation
Another example is the motion of blades of a fan

3. Combined rotation and translation motion

In this type of motion, the body is having both rotation and translation motion.

• Rolling

 In the case of rolling motion, a body rotates about a fixed axis, and the axis of rotation also moves.

Example- Rolling of football on the ground

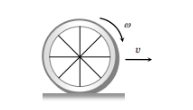
Here friction between the body and surface = $f \neq 0$

1. Kinetic energy-

   The total kinetic energy of the body is the sum of both translational and rotational kinetic energy.

   $
   K_{n e t}=K_T+K_R=\frac{1}{2} m V^2+\frac{1}{2} I \omega^2
   $

   
   Using $V=\omega R$ and $I=m K^2$

   $
   K_{n e t}=K_T+K_R=\frac{1}{2} m V^2\left(1+\frac{K^2}{R^2}\right)
   $

   2. Net Velocity at a point-

   $
   \vec{V}_{\text {net }}=\vec{V}_{\text {translation }}+\vec{V}_{\text {rotation }}
   $

   
   Where, $\vec{V}_{r o t}=r w$

Angular momentum is always calculated at a particular point.

The net Angular momentum of a body is the sum of angular momentum due to both translational and rotational motion.

    $\begin{aligned} \vec{L} & =L_{\text {com }}+m\left(\vec{r} \times v_{\text {com }}\right) \\ \Rightarrow \vec{L} & =I_{\text {com }} \vec{\omega}+m\left(\vec{r} \times v_{\text {com }}\right)\end{aligned}$

Where $L_{com}$ represents the angular momentum of the body about the centre of mass and r is the position vector about which we have to calculate the angular momentum.