Centre Of Mass Of Semicircular Ring MCQ - Practice Questions & Answers

Concepts Covered - 1

Position of centre of mass for semicircular ring

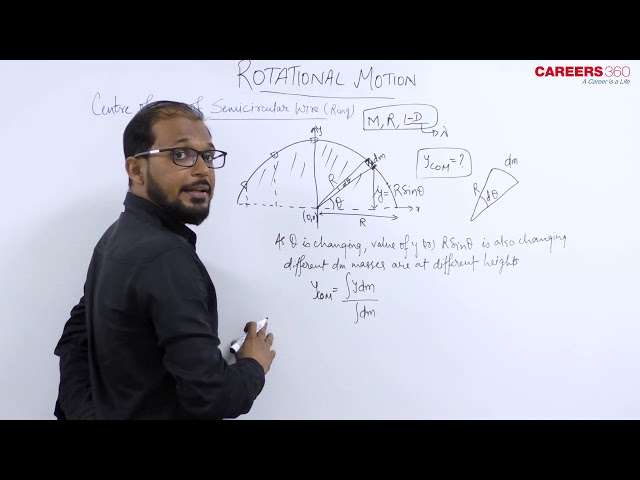
Have a look at the figure of semicircular ring.

Since it is symmetrical about y-axis on both sides of the origin

So we can say that its $x_{cm} = 0$

And its $z_{cm} = 0$ as z-coordinate is zero for all particles of semicircular ring.

Now, we will calculate its $y_{cm}$ which is given by

$y_{cm} = \frac{\int y.dm}{\int dm}$

So , Take a small elemental arc of mass dm at an angle $\theta$ from the x-direction.

Its angular width d $\theta$

If the radius of the ring is R then its y coordinate will be Rsin $\theta$

So, $dm=\frac{M}{\pi R}*Rd\theta =\frac{M}{\pi }d\theta$

As, $y_{cm} = \frac{\int y.dm}{\int dm}$

So, $y_{cm}=\frac{\int_{0 }^{\pi}\frac{M}{\pi R}\times R\times Rsin\theta d\theta}{M}=\frac{R}{\pi }\int_{0 }^{\pi}sin\theta d\theta=\frac{2R}{\pi }$

UPES B.Tech Admissions 2025

Apply

Ranked #42 among Engineering colleges in India by NIRF | Highest CTC 50 LPA , 100% Placements

Amrita University B.Tech 2025

Apply

Recognized as Institute of Eminence by Govt. of India | NAAC ‘A++’ Grade | Upto 75% Scholarships

Dayananda Sagar University B.Tech Admissions 2025

Apply

60+ Years of Education Legacy | UGC & AICTE Approved | Prestigious Scholarship Worth 6 Crores | H-CTC 35 LPA

Parul University B.Tech Admissions 2025

Apply

India's youngest NAAC A++ accredited University | NIRF rank band 151-200 | 2200 Recruiters | 45.98 Lakhs Highest Package

Lovely Professional University B.Tech Admissions 2025

Apply

India's Largest University | NAAC A++ Accredited | 100% Placement Record | Highest Package Offered : 3 Cr PA

Atlas SkillTech University | B.Tech Admissions

Apply

Hands on Mentoring and Code Coaching | Cutting Edge Curriculum with Real World Application

Centre Of Mass Of Semicircular Ring - Practice Questions & MCQ

Quick Facts

Concepts Covered - 1

Study it with Videos

Study other Related Concepts

Centre Of Mass Of Semicircular Ring Current Topic

Get Answer to all your questions

JEE Main Articles

B.Tech/B.Arch Admissions OPEN

UPES B.Tech Admissions 2025

Amrita University B.Tech 2025

Dayananda Sagar University B.Tech Admissions 2025

Parul University B.Tech Admissions 2025

Lovely Professional University B.Tech Admissions 2025

Atlas SkillTech University | B.Tech Admissions

Explore on Careers360

JEE Main

JEE Advanced

AP EAMCET

TS EAMCET

MHT CET

KCET

VITEEE

BITSAT

Colleges By Degree

Colleges By Branches

Colleges By Exam

By City

By State

BE/B.Tech

Diploma

Download Careers360 App

All this at the convenience of your phone

Scan and download the app