Real Gas And Equation - Practice Questions & MCQ

Consider an ideal gas (consisting of N molecules each of mass m) enclosed in a cubical box of side L as shown in the below figure.

1. Instantaneous velocity- 

Any molecule of gas moves with velocity $\vec{v}$ in any direction
where $\quad \vec{v}=v_x \hat{i}+v_y \hat{j}+v_z \hat{k}$
And Due to the random motion of the molecule

$
\begin{aligned}
& v_x=v_y=v_z \\
& A s v=\sqrt{v_x^2+v_y^2+v_z^2} \\
& \Rightarrow v=3 v_x^2=3 v_y^2=3 v_z^2
\end{aligned}
$

2. The time during a collision-Time between two successive collisions with the wall $A_1$

$
\begin{aligned}
& \text { I.e } \Delta t=\frac{\text { Distance travelled by molecule between two successive collision }}{\text { Velocity of molecule }} \\
& \text { or } \quad \Delta t=\frac{2 L}{v_x}
\end{aligned}
$

3. Collision frequency $(\mathbf{n})$ : It means the number of collisions per second.

$
\text { I.e } n=\frac{1}{\Delta t}=\frac{v_x}{2 L}
$

4. Change in momentum: This molecule collides with $A_1$ wall (A1) with velocity $v_x$ and rebounds with velocity ( $-\mathrm{v}_{\mathrm{x}}$ ) The change in momentum of the molecule is given by

$
\Delta p=\left(-m v_x\right)-\left(m v_x\right)=-2 m v_x
$
 

As the momentum remains conserved in a collision,

 

$
\begin{aligned}
& \Delta p_{\text {system }}=0 \\
& \Delta p_{\text {system }}=\Delta p_{\text {molecule }}+\Delta p_{\text {wall }}=0 \\
& \Delta p_{\text {wall }}=-\Delta p_{\text {molecule }}
\end{aligned}
$

the change in momentum of wall $\mathrm{A}_1$ is $\Delta p=2 m v_x$
5. Force on the wall: Force exerted by a single molecule on the $\mathrm{A}_1$ wall is equal to the rate at which the momentum is transferred to the wall by this molecule.
i.e. $F_{\text {Single molecule }}=\frac{\Delta p}{\Delta t}=\frac{2 m v_x}{\left(2 L / v_x\right)}=\frac{m v_x^2}{L}$

The total force on the wall $\mathrm{A}_1$ due to N molecules

$
F_x=\frac{m}{L} \sum v_x^2=\frac{m}{L}\left(v_{x_1}^2+v_{x_2}^2+v_{x 3}^2+\ldots\right)=\frac{m N}{L} \overline{v_x^2}
$

where $\overline{v_x^2}=$ mean square of $x$ component of the velocity.
6. Pressure-As pressure is defined as force per unit area, hence the pressure on $\mathrm{A}_1$ wall

$
\begin{aligned}
& P_x=\frac{F_x}{A}=\frac{m N}{A L} \overline{v_x^2}=\frac{m N}{V} \overline{v_x^2} \\
& \text { As } \overline{v_x^2}=\overline{v_y^2}=\overline{v_z^2} \\
& \text { So } \overline{v^2}=\overline{v_x^2}+\overline{v_y^2}+v_z^2 \\
& \Rightarrow \overline{v_x^2}=\overline{v_y^2}=\overline{v_z^2}=\frac{v^2}{3}
\end{aligned}
$
 

So Total pressure inside the container is given by

$
P=\frac{1}{3} \frac{m N}{V} \overline{v^2}=\frac{1}{3} \frac{m N}{V} v_{r m s}^2 \quad\left(\text { where } v_{r m s}=\sqrt{\overline{v^2}}\right)
$

Using total mass $=\mathrm{M}=\mathrm{mN}$
Pressure due to an ideal gas is given as

$
P=\frac{1}{3} \rho v_{r m s}^2=\frac{1}{3}\left(\frac{M}{V}\right) \cdot v_{r m s}^2

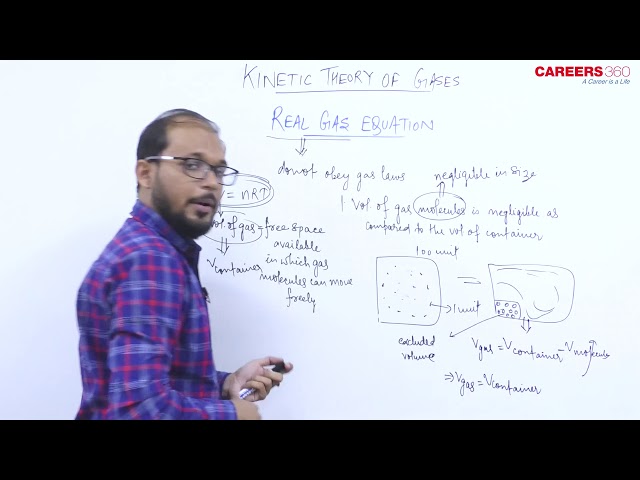
• Real gas- The gases which do not obeys gas Laws are called Real gas.

Two main factors because of which Real gas deviates from ideal gas are:

1)   Presence of force of attraction between molecules.

2)    The size of molecules are not negligible.

The gases actually found in nature are called real gases.

   

From the ideal gas equation, we get
For exactly one mole of an ideal gas $\frac{P V}{R T}=1$
PV

The quantity $\overline{R T}$ is called the compressibility factor and should be a unit for an ideal gas.

$
P V
$

Plotting the experimentally determined value of $\overline{R T}$ for exactly one mole of various real gases as a function of pressure P shows a deviation from identity as shown in the below graph.

                

     Similarly, real gases show deviation from ideal behavior as a function of temperature as shown in the below graph.

  

From the above graphs, we can say that A real gas behaves as an ideal gas most closely at low pressure and high temperature.
- Real gas equation- Real gas equation, For n moles of gas is given by

$
\left(P+\frac{n^2 a}{V^2}\right)(V-n b)=n R T
$

Where a and b are called Vander wall's constant having dimensions and units as follows:
Dimension : $[a]=\left[M L^5 T^{-2}\right]$ and $[b]=\left[L^3\right]$ Dimension : $[a]=\left[M L^5 T^{-2}\right]$ and $[b]=\left[L^3\right]$
Units : $a=N \times m$ and $b=m^3$ Units : $a=N \times m$ and $b=m^3$

As we know the ideal gas equation as $P V=n R T$.
From equations (1) and (2) we can say that
The real gas equation is nothing but the ideal gas equation with two corrections (i.e Volume correction and Pressure correction)
These corrections are given by Vander Waal's. So the real gas equation is also known as Vander Waal's gas equation.
1. Volume correction- Due to the finite size of the molecules the effective volume of gas becomes (V-nb).
2. Pressure correction- Due to the presence of intermolecular force in real gases, the effective pressure of gas becomes

$
P+\frac{n^2 a}{V^2}
$
 

 

     

                                                                                            

 

 

 

$

 

where
$m=$ mass of one molecule
$\mathrm{N}=$ Number of the molecule

$
v_{r m s}^2=\frac{v_1^2+v_2^2+\ldots \ldots \ldots}{n}
$

$v_{r m s}=\mathrm{RMS}$ velocity