Amity University-Noida B.Tech Admissions 2026
Among top 100 Universities Globally in the Times Higher Education (THE) Interdisciplinary Science Rankings 2026
Ideal gas equation is considered one of the most asked concept.
78 Questions around this concept.
Which of the following shows the correct relationship between the pressure ‘P’ and density ρ of an ideal gas at constant temperature?
‘n’ moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will be :

Which of the following graphs represent the behavior of an ideal gas? Symbols have their usual meaning.
New: JEE Main 2026 City Intimation Slip Link
JEE Main Sample Papers: Physics | Chemistry | Maths | Top 30 Repeated Questions
JEE Main QP & Mock: Previous 10 Year Questions | Chapter Wise PYQs | Mock test Series
For the P-V diagram given for an ideal gas,

out of the following which one correctly represents the T-P diagram ?
Which of the following diagrams (figure) depicts ideal gas behaviour?
One mole of an ideal gas undergoes a linear process as shown in the figure below. Its temperature expressed as a function of volume V is,
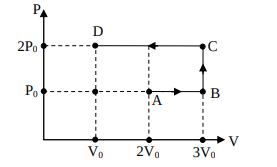
Using the given P-V diagram, the work done by an ideal gas along the path ABCD is-
The equation which relates the pressure (P), volume (V) and temperature (T) of the given state of an ideal gas is known as an ideal gas equation or equation of state.
From Boyle's law, we get
$
V \propto \frac{1}{P}
$
and From Charle's Law, we get $V \propto T$.
And from Avogadro's Law, we get $V \propto n$
And from equation (1), (2), (3)
we can write
$
\begin{aligned}
& V \propto \frac{n T}{P} \\
& \text { or } \frac{P V}{n T}=\text { constant } \\
& \text { or } \frac{P V}{n T}=R(\text { where } R \text { is proportionality constant }) \\
& \text { or } P V=n R T
\end{aligned}
$
So Ideal Gas Equation is given as
$
P V=n R T
$
where
T= Temperature
P= pressure of ideal gas
V= volume
n= numbers of mole
R = universal gas constant
At S.T.P. the value of the universal gas constant is the same for all gases.
And its value is given as
$
R=8.31 \frac{\text { Joule }}{\text { mole } \times \text { Kelvin }}=2 \frac{\mathrm{cal}}{\text { mole } \times \text { Kelvin }}
$
And its Dimension is : $\left[M L^2 T^{-2} \theta^{-1}\right]$
- Boltzman's constant (k)-
It is represented by per mole gas constant.
$
\text { i.e } k=\frac{R}{N}=\frac{8.31}{6.023 \times 10^{23}}=1.38 \times 10^{-23} \mathrm{~J} / \mathrm{K}
$
- Specific gas constant (r)-
It is represented by per gram gas constant.
i.e. $\quad r=\frac{R}{M}$
It's unit is $\frac{\text { Joule }}{\mathrm{gm} \times \text { kelvin }}$
"Stay in the loop. Receive exam news, study resources, and expert advice!"
