Radical Axis - Practice Questions & MCQ

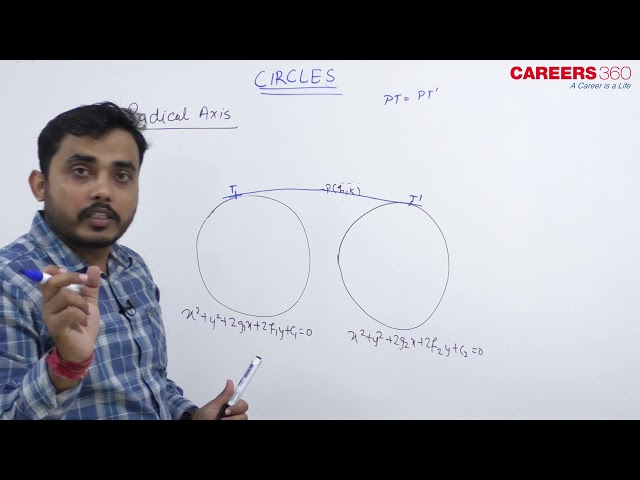
Radical Axis

The radical axis of two circles is the locus of a point which moves in a plane in such a way that the lengths of the tangents drawn from it to the two circles are the same.
Consider the two circles:

$
\begin{aligned}
& S_1: x^2+y^2+2 g_1 x+2 f_1 y+c_1=0 \\
& S_2: x^2+y^2+2 g_2 x+2 f_2 y+c_2=0
\end{aligned}
$

Let point $\mathrm{P}\left(\mathrm{x}_1, \mathrm{y}_1\right)$ such that

$
|\mathrm{PA}|=|\mathrm{PB}|
$

The length of the tangent from a point $\mathrm{P}\left(\mathrm{x}_1, \mathrm{y}_1\right)$ to circle S is $\sqrt{S_1}$

$
\Rightarrow \sqrt{x_1^2+y_1^2+2 g_1 x_1+2 f_1 y_1+c_1}=\sqrt{x_1^2+y_1^2+2 g_2 x_1+2 f_2 y_1+c_2}
$
Square both sides, and we get

$
\begin{aligned}
& \Rightarrow \mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{~g}_1 \mathrm{x}_1+2 \mathrm{f}_1 \mathrm{y}_1+\mathrm{c}_1=\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{~g}_2 \mathrm{x}_1+2 \mathrm{f}_2 \mathrm{y}_1+\mathrm{c}_2 \\
& \Rightarrow 2 \mathrm{x}_1\left(\mathrm{~g}_1-\mathrm{g}_2\right)+2 \mathrm{y}_1\left(\mathrm{f}_1-\mathrm{f}_2\right)+\mathrm{c}_1-\mathrm{c}_2=0
\end{aligned}
$

This is the required equation of the radical axis.