Projectile Motion - Practice Questions & MCQ

• Projectile Motion- Two dimesional motion under action of uniform force is called is called projectile motion.

                E.g-  A javelin thrown by an athlete 

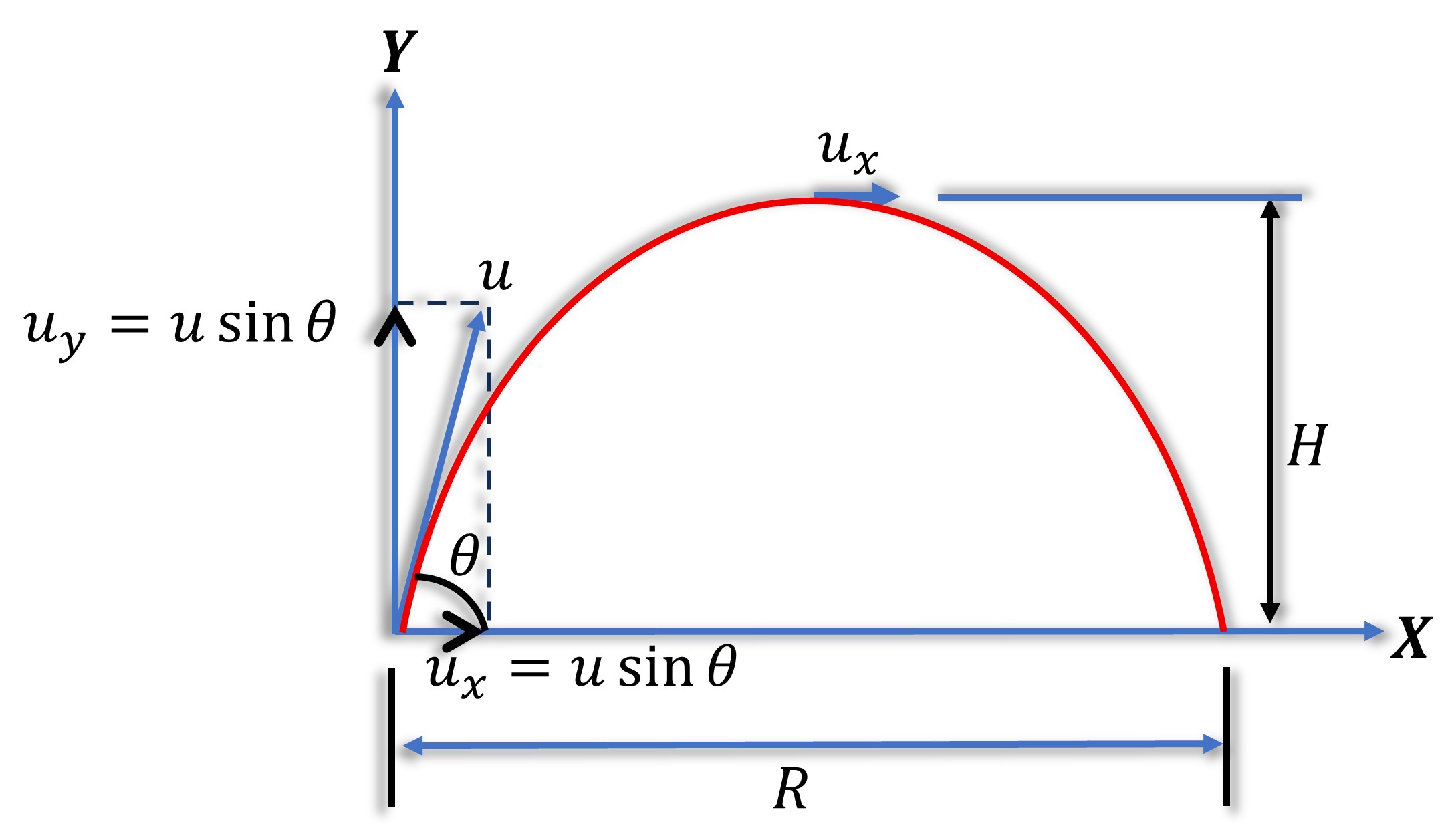
1. Projectile Projected at an angle $\theta$
- Initial Velocity- u

Horizontal component $=u_x=u \cos \theta$
Vertical component $=u_y=u \sin \theta$
- Final velocity $=\mathrm{V}$

Horizontal component $=V_x=u \cos \theta$
Vertical component $=V_y=u \sin \theta-g . t$
So,

$
V=\sqrt{V_x^2+V_y^2}
$

- Displacement $=\mathrm{S}$

Horizontal component $=S_x=u \cos \theta . t$
Vertical component $=S_y=u \sin \theta \cdot t-\frac{1}{2} \cdot g \cdot t^2$
and,

$
S=\sqrt{S_x^2+S_y^2}
$

- Acceleration $=\mathrm{a}$

Horizontal component $=0$
Vertical component $=-\mathrm{g}$
So, $a=-g$

Parameters in Projectile motion - 

1. Maximum Height - 

• Maximum vertical distance attained by a projectile during its journey.

• - Formula-

  $
  H=\frac{U^2 \sin ^2 \theta}{2 g}
  $

  - When the velocity of projectile increases n time then Maximum height is increased by a factor of $n^2$
  - Special Case-

  If U is doubled, H becomes four times provided $\theta \& \mathrm{~g}$ are constant.
  2) Time of Flight
  - Time for which projectile remains in the air above the horizontal plane.
  - Formula-
  1. $T=\frac{2 u \sin \theta}{g}$
  2. Time of ascent $=$

  $
  t_a=\frac{T}{2}
  $

  3. Time of descent =

  $
  t_d=\frac{T}{2}
  $
   

• When the velocity of projectile increased n time then Time of ascent becomes n times

• When the velocity of projectile increased n time then Time of descent becomes n times

• When the velocity of the projectile increased n time then the time of flight becomes n times.

3. Horizontal Range

• Horizontal distance travelled by projectile from the point of the projectile to the point on the ground where its hits.

• Formula-

$
R=\frac{u^2 \sin 2 \theta}{g}
$

- Special case of horizontal range
1. For max horizontal range.

$
\begin{aligned}
\theta & =45^0 \\
R_{\max } & =\frac{u^2 \sin 2(45)}{g}=\frac{u^2 \times 1}{g}=\frac{u^2}{g}
\end{aligned}
$

2. Range remains the same whether the projectile is thrown at an angle $\theta$ with the horizontal or at an angle $\theta$ with vertical ( $90-\theta$ ) with horizontal
3. When the velocity of projectile increases $n$ time then the horizontal range is increased by a factor of $n^2$
4. When the horizontal range is $n$ times the maximum height then

$
\tan \theta=\frac{4}{n}
$
 

• Equation of trajectory-
• 
• $y=x \tan \theta-\frac{g x^2}{2 u^2 \cos ^2 \theta}$