Mathematical Tools - Practice Questions & MCQ

1. Differentiation

Differentiation is very useful when we have to find rates of change of one quantity compared to another.

• If y is one quantity and we have to find the rate of change of y with respect to x which is another quantity 

Then the differentiation of y w.r.t x is given as $\frac{d y}{d x}$

• For a y V/s x graph 

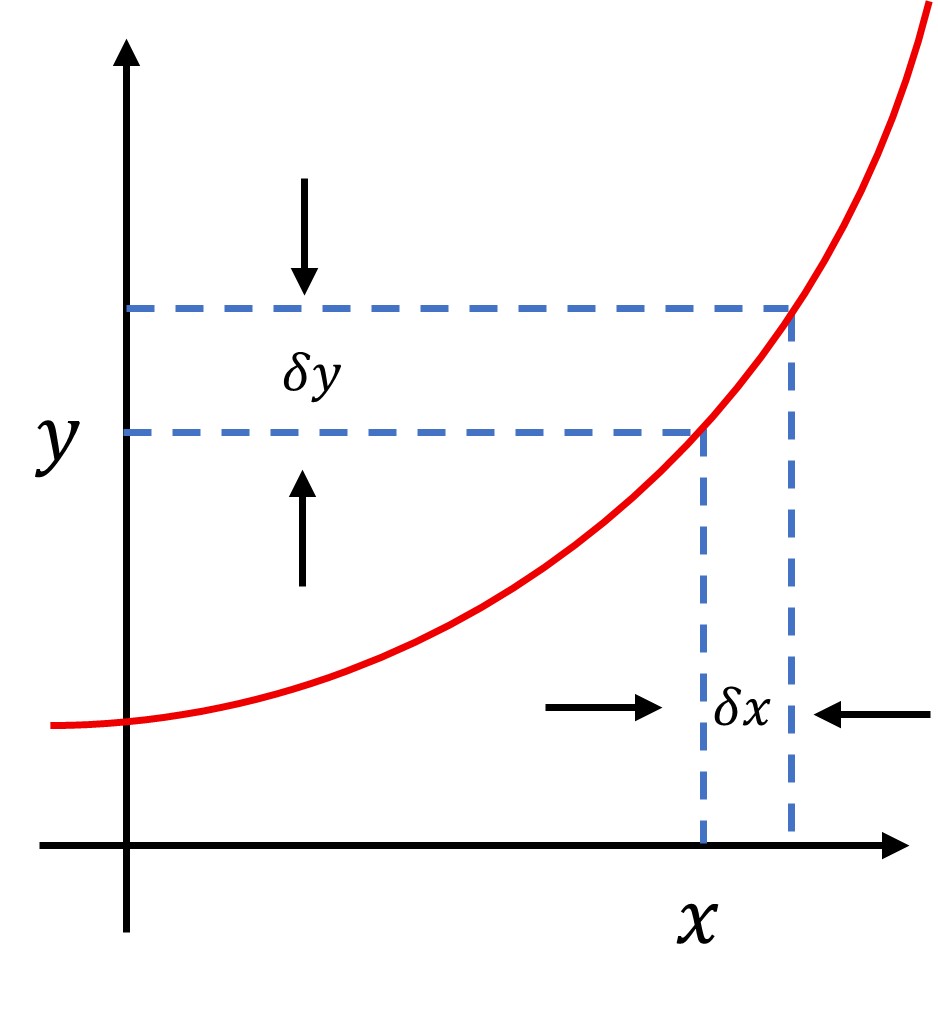
We can find the slope of graph using differentiation

1.e Slope of $\mathrm{y} \mathrm{V} / \mathrm{s} \times$ graph $=\frac{d y}{d x}$
- Some important Formulas of differentiation

$
\begin{aligned}
& \quad \cdot \frac{d}{d x}\left(x^n\right)=n x^{n-1} \\
& \text { Example- } \\
& \frac{d}{d x}\left(x^5\right)=(n=5) \\
& \because \frac{\mathrm{d} x^n}{\mathrm{~d} x}=n x^{n-1} \\
& \therefore \frac{\mathrm{~d} x^5}{\mathrm{~d} x}=5 x^{5-1} \\
& \Rightarrow \frac{\mathrm{~d} x^5}{\mathrm{~d} x}=5 x^4
\end{aligned}
$
 

Similarly 

           $\begin{aligned} & \frac{d}{d x} \sin x=\cos x \\ & \frac{d}{d x} \cos x=-\sin x \\ & \frac{d}{d x} \tan x=\sec ^2 x \\ & \frac{d}{d x} \cot x=-\csc ^2 x \\ & \frac{d}{d x} \sec x=\sec x \tan x \\ & \frac{d}{d x} \csc x=-\csc x \cot x \\ & \frac{d}{d x} e^x=e^x \\ & \frac{d}{d x} a^x=a^x \ln a \\ & \frac{d}{d x} \ln |x|=\frac{1}{x}\end{aligned}$

2. Integration

•  Opposite process of differentiation is known as integration.

• Let  x, y are two quantities

Using differentiation we can find the rate of change of y with respect to x

Which is given by $\frac{d y}{d x}$
But using integration we can get direct relationship between quantities x and y
So let $\frac{d y}{d x}=K \underset{\text { where } \mathrm{K} \text { is constant }}{ }$
Or we can write $d y=K d x$
Now integrating on both sides we get direct relationship between $x$ and $y$
I.e $\int d y=\int K d x$
$y=K x+C$

Where C is some constant 

• For a y V/s x graph 

We can find the area of graph using integration

• Some important Formulas of integration

• $
  \begin{aligned}
  & \text {. } \int x^n d x=\frac{x^{n+1}}{n+1}+C \text { where (C = constant) } \\
  & \text { E.g- } \int x^n d x=, \quad n=3 \\
  & \Rightarrow \frac{x^{n+1}}{n+1}+C \\
  & \Rightarrow \frac{x^{3+1}}{3+1}+C \\
  & \Rightarrow \frac{x^4}{4}+C \\
  & \int \frac{d x}{x}=\ln |x|+C \\
  & \int e^x d x=e^x+C \\
  & \int a^x d x=\frac{1}{\ln a} a^x+C \\
  & \text { - } \int \ln x d x=x \ln x-x+C \\
  & \int \sin x d x=-\cos x+C \\
  & \int \cos x d x=\sin x+C \\
  & \int \tan x d x=-\ln |\cos x|+C \\
  & \int \cot x d x=\ln |\sin x|+C \\
  & \int \sec x d x=\ln |\sec x+\tan x|+C \\
  & \text { - } \int \csc x d x=-\ln |\csc x+\cot x|+C \\
  & \int \sec ^2 x d x=\tan x+C \\
  & \int \csc ^2 x d x=-\cot x+C \\
  & \int \sec x \tan x d x=\sec x+C \\
  & \text { - } \int \csc x \cot x d x=-\csc x+C \\
  & \int \frac{d x}{\sqrt{a^2-x^2}}=\sin ^{-1} \frac{x}{a}+C
  \end{aligned}
  $