Position of a point with respect to Ellipse - Practice Questions & MCQ

Position of a point with respect to Ellipse

P(x₁,y₁) is any point in the plane

Then,

a) P lies outside of the ellipse, then $\frac{x^2}{a^2}+\frac{y^2}{b^2}-1>0$
(b) P lies on of the ellipse, then $\frac{x^2}{a^2}+\frac{y^2}{b^2}-1=0$
(c) P lies inside of the ellipse, then $\frac{x^2}{a^2}+\frac{y^2}{b^2}-1<0$

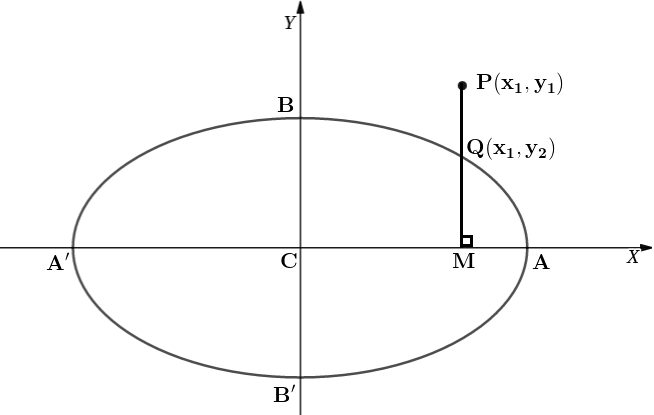
Consider the figure, Point $Q\left(x_1, y_2\right)$ lying on the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
then,

$
\begin{array}{ll} 
& \frac{\mathrm{x}_1^2}{\mathrm{a}_2}+\frac{\mathrm{y}_2^2}{\mathrm{~b}^2}=1 \\
\Rightarrow \quad & \frac{\mathrm{y}_2^2}{\mathrm{~b}^2}=1-\frac{\mathrm{x}_1^2}{\mathrm{a}_2}
\end{array}
$
Now, point P lies outside the ellipse, on the ellipse or inside the ellipse according as

$
\begin{array}{ll} 
& \text { PM }>,=\text { or }<\mathrm{PQ} \\
\Rightarrow & \mathrm{y}_1>,=\text { or }<\mathrm{y}_2 \\
\Rightarrow & \frac{\mathrm{y}_1^2}{\mathrm{~b}^2}>=\text { or }<\frac{\mathrm{y}_2^2}{\mathrm{~b}^2} \\
\Rightarrow & \frac{\mathrm{y}_1^2}{\mathrm{~b}^2}>=\text { or }<1-\frac{\mathrm{x}_1^2}{\mathrm{a}^2} \quad \text { [From eq (1)] } \\
\Rightarrow & \frac{\mathrm{x}_1^2}{\mathrm{x}^2}+\frac{\mathrm{y}_1^2}{\mathrm{~b}^2}>,=\text { or }<1 \\
\Rightarrow & \frac{\mathrm{x}_1^2}{\mathrm{x}^2}+\frac{\mathrm{y}_1^2}{\mathrm{~b}^2}-1>,=\text { or }<0
\end{array}
$

As Point P(x₁, y₁) lies outside, on or inside the ellipse according to  $\frac{\mathrm{x}_1^2}{\mathrm{a}^2}+\frac{\mathrm{y}_1^2}{\mathrm{~b}^2}-1>$, or $<0$.