Foot of Perpendicular and Image - Practice Questions & MCQ

Foot of Perpendicular

Foot of perpendicular of $P\left(x_1, y_1\right)$ on the line $A B$ : $a x+b y+c=0$ is $M\left(x_2, y_2\right)$. then

$
\frac{\mathrm{x}_2-\mathrm{x}_1}{\mathbf{a}}=\frac{\mathrm{y}_2-\mathrm{y}_1}{\mathbf{b}}=-\frac{\left(\mathrm{ax}_1+\mathrm{by}_1+\mathrm{c}\right)}{\left(\mathrm{a}^2+\mathrm{b}^2\right)}
$
Proof:
Let the coordinate of foot of perpendicular be $M\left(x_2, y_2\right)$. Then, point $M$ lies on the line $A B$.

$
\begin{aligned}
& \Rightarrow \quad \quad \mathrm{ax}_2+\mathrm{by}_2+\mathrm{c}=0 \\
& \text { and, } \quad \because \quad \text { PM } \perp \mathrm{AB} \\
& \text { then, }(\text { slope of PM) }(\text { slope of } \mathrm{AB})=-1 \\
& \Rightarrow \quad\left(\frac{\mathrm{y}_2-\mathrm{y}_1}{\mathrm{x}_2-\mathrm{x}_1}\right)\left(-\frac{\mathrm{a}}{\mathrm{~b}}\right)=-1 \\
& \text { or } \quad \frac{\mathrm{x}_2-\mathrm{x}_1}{\mathrm{a}}=\frac{\mathrm{y}_2-\mathrm{y}_1}{\mathrm{~b}}
\end{aligned}
$
Using ratio and proportion

$
\begin{aligned}
& \frac{x_2-x_1}{a}=\frac{y_2-y_1}{b}=\frac{a\left(x_2-x_1\right)+b\left(y_2-y_1\right)}{a^2+b^2} \\
& \frac{x_2-x_1}{a}=\frac{y_2-y_1}{b}=-\frac{\left(a x_1+b y_1+c\right)}{a^2+b^2}
\end{aligned}
$

(Using (i))

Image of a Point about a Line

$\mathrm{Q}\left(\mathrm{x}_2, \mathrm{y}_2\right)$ is the image of a point $\mathrm{P}\left(\mathrm{x}_1, \mathrm{y}_1\right)$ about a line $\mathrm{L}: \mathrm{ax}+\mathrm{by}+\mathrm{c}=0$. To find the coordinates of point $Q$, first find the coordinates of the foot of perpendicular $M$ drawn from the point $P\left(x_1, y_1\right)$ on the line $L$ and use the concept that point $M$ is the midpoint of point $P\left(x_1, y_1\right)$ and point $Q\left(x_2, y_2\right)$.

OR
If the Image of $\mathrm{P}\left(\mathrm{x}_1, \mathrm{y}_1\right)$ on the line $\mathrm{L}: \mathrm{ax}+\mathrm{by}+\mathrm{c}=0$ is $\mathrm{Q}\left(\mathrm{x}_2, \mathrm{y}_2\right)$, then

$
\frac{\mathrm{x}_2-\mathrm{x}_1}{\mathbf{a}}=\frac{\mathrm{y}_2-\mathrm{y}_1}{\mathbf{b}}=-\frac{2\left(\mathrm{ax}_1+\mathrm{by}_1+\mathrm{c}\right)}{\left(\mathrm{a}^2+\mathrm{b}^2\right)}
$

Image of a point in some standard lines

1. Image of $P(h, k)$ with respect to $X$-axis is $Q=(h,-k)$

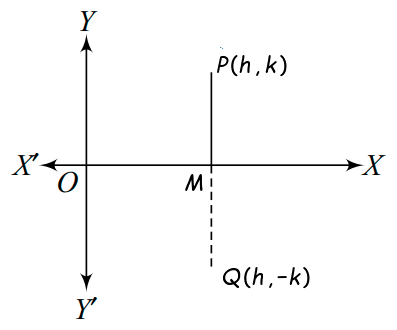
2. Image of $\mathrm{P}(\mathrm{h}, \mathrm{k})$ with respect to Y -axis is $\mathrm{Q}=(-\mathrm{h}, \mathrm{k})$

3. Image of $P(h, k)$ with respect to the line $x=y$ is $Q=(k, h)$

Reflection of Light

Laws of reflection
1. The incident ray, the normal ray and the reflected ray to a surface at the point of an incident all lie on the same plane.
2. The angle of incident = angle of reflection

$
\angle \mathrm{i}=\angle \mathrm{r}
$