Equation of Normal in Point Form and Parametric Form - Practice Questions & MCQ

Equation of Normal in Point Form and Parametric Form

Point form

The equation of normal at $\left(x_1, y_1\right)$ to the ellipse, $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is $\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2$.

Proof:

We know that the equation of tangent in point from at $\left(\mathrm{x}_1, \mathrm{y}_1\right)$

$
\frac{x x_1}{a^2}+\frac{y y_1}{b^2}=1
$
Slope of tangent at $\left(x_1, y_1\right)$ is $-\frac{b^2 x_1}{a^2 y_1}$
$\therefore \quad$ Slope of normal at $\left(\mathrm{x}_1, \mathrm{y}_1\right)$ is $\frac{\mathrm{a}^2 \mathrm{y}_1}{\mathrm{~b}^2 \mathrm{x}_1}$
Hence, the equation of normal at point $\left(\mathrm{x}_1, \mathrm{y}_1\right)$ is

$
\left(\mathrm{y}-\mathrm{y}_1\right)=\frac{\mathrm{a}^2 \mathrm{y}_1}{\mathrm{~b}^2 \mathrm{x}_1}\left(\mathrm{x}-\mathrm{x}_1\right)
$

or $\quad \frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2$

Parametric form
The equation of normal at $(a \cos \theta, b \sin \theta)$ to the ellipse, $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is $a x \sec \theta-b y \csc \theta=a^2-b^2$

Proof:

In the equation of point form of normal, replace $\mathrm{x}_1$ with $a \cdot \cos \theta$ and $\mathrm{y}_1$ with $\mathrm{b} \cdot \sin \theta$.

$
\begin{aligned}
& \frac{\mathrm{a}^2 \mathrm{x}}{\mathrm{x}_1}-\frac{\mathrm{b}^2 \mathrm{y}}{\mathrm{y}_1}=\mathrm{a}^2-\mathrm{b}^2 \\
& \mathrm{x}_1 \rightarrow \mathrm{a} \cos \theta \\
& \mathrm{y}_1 \rightarrow \mathrm{~b} \sin \theta \\
& \frac{\mathrm{a}^2 \mathrm{x}}{\mathrm{a} \cos \theta}-\frac{\mathrm{b}^2 \mathrm{y}}{\mathrm{~b} \sin \theta}=\mathrm{a}^2-\mathrm{b}^2 \\
& \mathrm{ax} \sec \theta-\mathrm{by} \csc \theta=\mathrm{a}^2-\mathrm{b}^2
\end{aligned}
$
 

Equation of Normal in Slope form

The equation of normal of slope m to the ellipse, $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ $y=m x \mp \frac{m\left(a^2-b^2\right)}{\sqrt{a^2+m^2 b^2}}$ and coordinate of point of contact is $\left( \pm \frac{a^2}{\sqrt{a^2+m^2 b^2}}, \pm \frac{m b^2}{\sqrt{a^2+m^2 b^2}}\right)$

We know that the equation of normal of the ellipse in point form $\left(\mathrm{x}_1, \mathrm{y}_1\right)$ is

$
\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2
$
Let ' $m$ ' be the slope of the normal (i), then

$
\begin{aligned}
\mathrm{m} & =\frac{\mathrm{a}^2 \mathrm{y}_1}{\mathrm{~b}^2 \mathrm{x}_1} \\
\Rightarrow \quad \mathrm{y}_1 & =\frac{\mathrm{b}^2 \mathrm{x}_1 \mathrm{~m}}{\mathrm{a}^2}
\end{aligned}
$
Since, $\left(\mathrm{x}_1, \mathrm{y}_1\right)$ lies on on the ellipse, then

$
\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}=1
$

put the value of $y_1$ in the above equation,

$
\frac{x_1^2}{a^2}+\frac{b^4 x_1^2 m^2}{a^4 b^2}=1 \quad \Rightarrow \quad \frac{x_1^2}{a^2}+\frac{b^2 x_1^2 m^2}{a^4}=1
$

or
from eq (ii) $\quad \mathrm{y}_1= \pm \frac{\mathrm{mb}^2}{\sqrt{\left(\mathrm{a}^2+\mathrm{b}^2 \mathrm{~m}^2\right)}}$
$\therefore$ equation of normal in in terms of 'm' is

$
\begin{aligned}
& y-\left( \pm \frac{m^2}{\sqrt{a^2+b^2 \mathrm{~m}^2}}\right)=m\left(x-\left( \pm \frac{a^2}{\sqrt{a^2+b^2 \mathrm{~m}^2}}\right)\right) \\
\Rightarrow \quad & y=m x \mp \frac{m\left(a^2-b^2\right)}{\sqrt{\left(a^2+b^2 \mathrm{~m}^2\right)}}
\end{aligned}
$
The coordinate of the point of contact is $\left( \pm \frac{a^2}{\sqrt{a^2+b^2 m^2}}, \pm \frac{m b^2}{\sqrt{a^2+b^2 m^2}}\right)$.

Pair of Tangents
The equation of pair of tangent from the point $\mathrm{P}\left(\mathrm{x}_1, \mathrm{y}_1\right)$ to the Ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is $\left(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\right)\left(\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}-1\right)=\left(\frac{x_1}{a^2}+\frac{y y_1}{b^2}-1\right)^2$ or, $\mathrm{SS}_1=\mathrm{T}^2$ where, $S=\frac{x^2}{a^2}+\frac{y^2}{b^2}-1$

$
\begin{aligned}
& \mathrm{S}_1=\frac{\mathrm{x}_1^2}{\mathrm{a}^2}+\frac{\mathrm{y}_1^2}{\mathrm{~b}^2}-1 \\
& \mathrm{~T}=\frac{\mathrm{xx}_1}{\mathrm{a}^2}+\frac{\mathrm{yy}_1}{\mathrm{~b}^2}-1
\end{aligned}
$

Where points Q and R are the point of contacts of the tangents to the ellipse.

Note:

The equation $\mathbf{S S}_{\mathbf{1}}=\mathbf{T}^{\mathbf{2}}$ can be used to find the combined equation of tangents for any general ellipse as well.

Chord of Contact:
The equation of chord of contact of tangents from the point $\mathrm{P}\left(\mathrm{x}_1, \mathrm{y}_1\right)$ to the Ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is $\frac{x_1}{a^2}+\frac{y_1}{b^2}=1$.

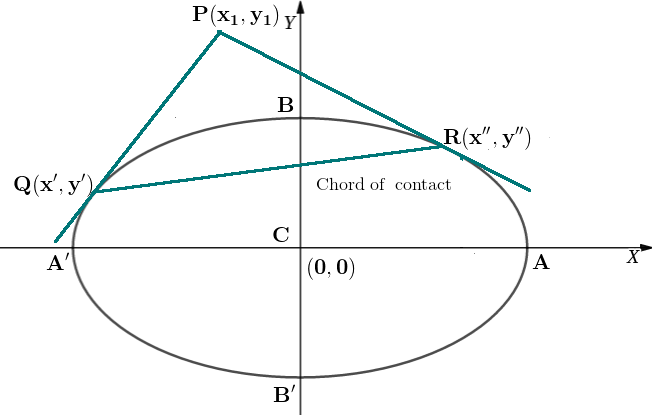
QR is a chord of contact.
Equation of Chord bisected at a given point
The equation of chord of the ellipse $\frac{x^2}{\mathrm{a}^2}+\frac{\mathrm{y}^2}{\mathrm{~b}^2}=1$ bisected at a given point $\mathrm{P}\left(\mathrm{x}_1, \mathrm{y}_1\right)$ is $\frac{\mathrm{xx}_1}{\mathrm{a}^2}+\frac{\mathrm{yy}_1}{\mathrm{~b}^2}-1=\frac{\mathrm{x}_1^2}{\mathrm{a}^2}+\frac{\mathrm{y}_1^2}{\mathrm{~b}^2}-1$
or, $\mathrm{T}=\mathrm{S}_1$

Note:

These formulae can be used for any general ellipse as well