Binding Energy Per Nucleon - Practice Questions & MCQ

Energy mass equivalence-

Einstein showed from his theory of special relativity that it is necessary to treat mass as another form of energy.

Einstein showed that mass is another form of energy and one can convert mass into other forms of energy, say kinetic energy and vice-versa. 

For this Einstein gave the famous mass-energy equivalence relation

$E=m c^2$ where c is the velocity of light in vacuum and $c=3 \times 10^8 \mathrm{~m} / \mathrm{s}$ or we can say $\Delta E=\Delta m c^2$
where $\Delta m=$ mass defect and $\Delta E=$ energy released
Note:

• For mass defect equal to 1 amu, the energy released is $\Delta E=(\Delta m) c^2=(1 \mathrm{amu}) \times\left(3 \times 10^8\right)^2=931.5 \mathrm{MeV}$
• A small amount of mass corresponds to a large amount of energy. Energy associated with the rest mass of an object is said to be its rest mass energy.

Rest mass of  an electron (me)	9.1 x 10-31 kg
	5.485 x 10-4 amu
Rest mass of a proton (mp)	1.6726 x 10-27 kg
	1.00727 amu
	1836.15 me
Rest mass of a neutron (mn)	1.6749 x 10-27 kg
	1.0086 amu
Energy equivalence of rest mass of an electron	0.51 MeV
Energy equivalence of rest mass of a proton	938.27 MeV
Energy equivalence of rest mass of a neutron	939.56 MeV

It is very useful to calculate energy emitted in the nuclear process.

Mass defect-

It is found that the mass of a nucleus is always less than the sum of masses of its constituent nucleons in a free state.

This difference in masses is called the mass defect.

Hence mass defect is given as 

$\Delta m=$ Sum of masses of nucleons- Mass of the nucleus
$\Delta m=\left[Z m_p+(A-Z) m_n\right]-M$
where
$m_p=$ Mass of proton, $m_n=$ Mass of each neutron,
$M=$ Mass of nucleus, $Z=$ Atomic number, $A=$ Mass number

Note- The mass of a typical nucleus is about $1 \%$ less than the sum of masses of nucleons.

Packing fraction -
Mass defect per atomic mass number is called packing fraction.
Packing fraction measures the stability of a nucleus. The smaller the value of the packing fraction, the larger is the stability of the nucleus.

Packing fraction $(f)=\frac{\Delta m}{A}=\frac{M-\left(Z m_p+(A-Z) m_n\right)}{A}$
$m_p=$ Mass of proton, $m_n=$ Mass of each neutron,
$M=$ Mass of nucleus, $Z=$ Atomic number, $A=$ Mass number

• Packing Fraction can have positive, negative, or zero value.

• Zero value of packing fraction is found in monoisotopic elements where the isotopic mass is equal to the mass number. For $8 \mathrm{O}^{16}$, $f \rightarrow$ zero

• Negative value of packing fraction indicates that there is a mass defect, hence binding energy. Such nuclei are stable.

• Positive values of Packing fraction are unstable undergoing fission and fusion processes.

 Nuclear binding energy (B.E)-

The neutrons and protons in a stable nucleus are held together by nuclear forces and energy is needed to pull them infinitely apart. This energy is called the binding energy of the nucleus.

OR 

Amount of energy released when nucleons come together to form a nucleus is called the binding energy of the nucleus.

OR

The binding energy of a nucleus may be defined as the energy equivalent to the mass defect of the nucleus.

If $\Delta m$ is a mass defect then according to Einstein's mass-energy relation
then

• Binding energy $=\Delta m \times c^2=\left[\left\{m_p Z+m_n(A-Z)\right\}-M\right] \times c^2 J$
• Binding energy $=\Delta m \times 931.5 \mathrm{MeV}$

 

 

To see how nucleon binding energy varies from nucleous to nucleous, it is important to compare the binding energy on nucleon basis. A more useful measure of the binding between protons and neutrons is the binding energy per nucleon or $\mathrm{E}_{b n}$. It is the ratio of the binding energy of a nucleus to the number of nucleons in the nucleus:

$$
\mathrm{E}_{\mathrm{bn}}=\frac{\mathrm{E}_{\mathrm{b}}}{\mathrm{~A}} \quad \text { or } \quad \mathrm{E}_{\mathrm{bn}}=\frac{\Delta \mathrm{Mc}^2}{\mathrm{~A}}
$$

where, A = Number of Nucleons.

We can define binding energy per nucleon theoretically as the average energy per nucleon needed to separate a nucleus into its individual nucleons.

Let’s look at a plot of the binding energy per nucleon versus the mass number for a large number of nuclei:

Following main features of the plot are:

1.  The maximum binding energy per nucleon is around 8.75 MeV for mass number $(A)=56$.
2.  The minimum binding energy per nucleon is around 7.6 MeV for mass number $(A)=238$.
3. The binding energy per nucleon, $\mathrm{E}_{\mathrm{bn}}$, is practically constant, i.e. practically independent of the atomic number for nuclei of middle mass number ( $30<A<170$ ).
4.  $E_{b n}$ is lower for both light nuclei $(A<30)$ and heavy nuclei $(A>170)$.
5. We can draw some conclusions from these four observations:

Conclusion 1

The force is attractive and sufficiently strong to produce a binding energy of a few MeV per nucleon.

Conclusion 2

• $\mathrm{E}_{b n}$ is nearly constant in the range $30<\mathrm{A}<170$ because the nuclear force is short-ranged. Consider a particular nucleon inside a sufficiently large nucleus. It will be under the influence of only some of its neighbours, which come within the range of the nuclear force.
• This means that all nucleons beyond the range of the nuclear force form $N_A$ will have no influence on the binding energy of $N_A$. So, we can conclude that if a nucleon has ' $p$ ' neighbours within the range of the nuclear force, then its binding energy is proportional to ' $p$ '.
• If we increase A by adding nucleons they will not change the binding energy of a nucleon inside. Since most of the nucleons in a large nucleus reside inside it and not on the surface, the change in binding energy per nucleon would be small.
• The binding energy per nucleon is a constant and is equal to pk , where k is a constant having the dimensions of energy. Also, the property that a given nucleon influences only nucleons close to it is also referred to as saturation property of the nuclear force.

Conclusion 3
A very heavy nucleus, say $A=240$, has lower binding energy per nucleon compared to that of a nucleus with $A=120$. Thus if a nucleus $A=240$ breaks into two $A=120$ nuclei, nucleons get more tightly bound. Also, in the process energy is released. This concept is used in Nuclear Fission.

Conclusion 4

Now consider two very light nuclei with $A<10$. If these two nuclei were to join to form a heavier nucleus, then the binding energy per nucleon of the fused and heavier nucleus would be more than the $\mathrm{E}_{\mathrm{bn}}$ of the lighter nuclei. So, the nucleons are more tightly bound post-fusion. Again energy would be released in such a process of fusion. This is the energy source of the sun,

Nuclear Force

Coulomb force is a force that determines the motion of atomic electrons. As in the previous concept, we have seen that for average mass nuclei the binding energy per nucleon is approximately 8 MeV, This is much larger than the binding energy in atoms. Hence, the nuclear force required to bind a nucleus together must be very strong and of a different type. It must be strong enough to overcome the repulsion between the (positively charged) protons and to bind both protons and neutrons into the tiny nuclear volume.

Le's look at the features of this force also called the nuclear binding force which is obtained from many experiments which were performed in between 1930 and 1950.

1. The nuclear force is much stronger than the Coulomb force acting between charges or the gravitational forces between masses. This is because the nuclear force needs to overpower the Coulomb repulsive force between the like-charged protons inside the nucleus. Hence, the nuclear force > the Coulomb force. Also, the gravitational force much weaker than the Coulomb force.
2. The nuclear force between two nucleons falls rapidly to zero as their distance is more than a few femtometres. This leads to a saturation of forces in a medium or a large-sized nucleus, which is the reason for the constancy of the binding energy per nucleon. Also, if the distance falls below 0.7fm, then this force becomes repulsive. A rough plot of the potential energy between two nucleons as a function of distance is shown below.

                 

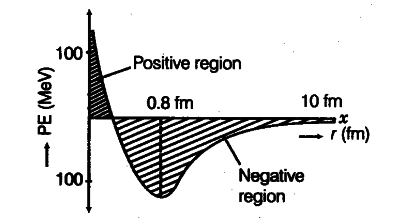
               The potential energy of two nucleons is a function of the distance between them.

If distance $>r_\alpha$, then nuclear force $=$ attractive
If distance $<r_\alpha$ the nuclear force $=$ repulsive

3. The nuclear force between neutron-neutron, proton-neutron and proton-proton is approximately the same. The nuclear force does not depend on the electric charge.

Nuclear Stability

Nuclear Stability is a concept that helps to identify the stability of an isotope. The two main factors that determine nuclear stability are the neutron/proton ratio (neutron to proton ratio.) and the total number of nucleons in the nucleus.

NEUTRON/PROTON RATIO

The graph below is a plot of the number of neutrons versus the number of protons in various stable isotopes. Stable nuclei with atomic numbers up to about 20 have an n/p ratio of about 1/1.

Above Z = 20, the number of neutrons always exceeds the number of protons in stable isotopes. The stable nuclei are located in the pink band known as the belt of stability. The belt of stability ends at lead-208.

NUMBER OF NUCLEONS

No nucleus higher than lead-208 is stable. That's because, although the nuclear strong force is about 100 times as strong as the electrostatic repulsions, it operates over only very short distances. When a nucleus reaches a certain size, the strong force is no longer able to hold the nucleus together.