Refraction At Spherical Surface - Practice Questions & MCQ

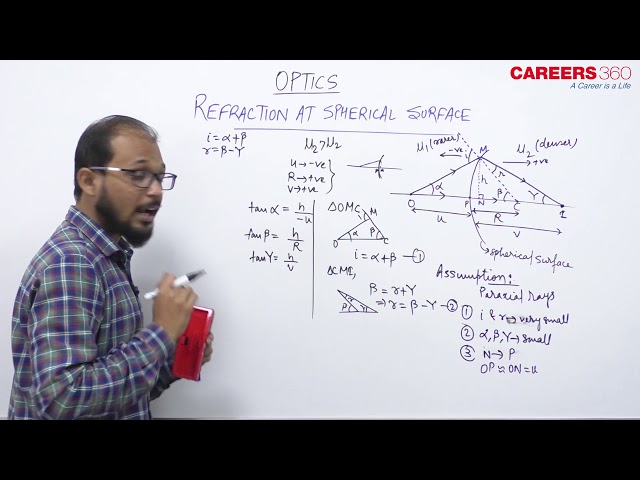
If an object 0 is placed in front of a curved surface as shown in the above figure, then the Refraction formula is given as

$$
\frac{n_2}{v}-\frac{n_1}{u}=\frac{n_2-n_1}{R}
$$

where
$n_1=\text { Refractive index of the medium from which light rays are coming (from the object). }$.
$n_2=$ Refractive index of the medium in which light rays are entering.
and $n_1<n_2$
and $\mathrm{u}=$ Distance of object, $\mathrm{v}=$ Distance of image, $\mathrm{R}=$ Radius of curvature
Note -
- use sign convention while solving the problem
- Real image forms on the side of a refracting surface that is opposite to the object, and virtual image forms on the same side as the object.
- Using $R=\infty$ (i.e for plane surface)
we get $\frac{n_2}{v}=\frac{n_1}{u} \Rightarrow \frac{n_2}{n_1}=\frac{v}{u}$

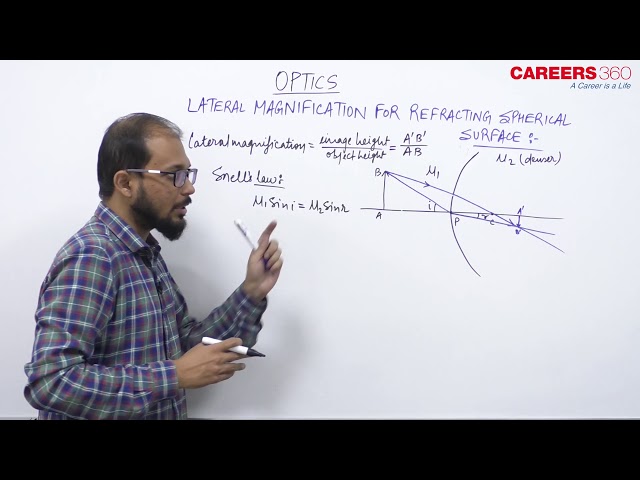
If an object AB is placed in front of a curved surface as shown in the above figure, then the lateral Magnification formula is given as

Lateral magnification, $m=\frac{\text { Image height }}{\text { Object height }}=\frac{-\left(A^{\prime} B^{\prime}\right)}{A B}$

$
m=-\frac{A^{\prime} B^{\prime}}{A B}=-\frac{\mu_1}{\mu_2} \times \frac{v}{u}=-\frac{v / \mu_2}{u / \mu_1}
$

where
$\mu_{1}=\text { Refractive index of the medium from which light rays are coming (from the object). }$
$\mu_{2}=\text { Refractive index of the medium in which light rays are entering. }$
and $\mu_1<\mu_2$
and $\mathrm{u}=$ Distance of object, $\mathrm{v}=$ Distance of image, $\mathrm{R}=$ Radius of curvature