MEDIUMAmity University-Noida B.Tech Admissions 2026
Among top 100 Universities Globally in the Times Higher Education (THE) Interdisciplinary Science Rankings 2026
Search Colleges, Exams, Schools & more
Login
Magnetic Moment Of Revolving Electron And Bohr Magneton - Practice Questions & MCQ
Edited By admin | Updated on Sep 18, 2023 18:34 AM | #JEE Main
Quick Facts
-
13 Questions around this concept.
Solve by difficulty
A uniform conducting wire of length is $24 a$, and resistance $R$ is wound up as a current carrying coil in the shape of an equilateral triangle of side ' $a$ ' and then in the form of a square of side ' $a$ '. The coil is connected to a voltage source $V_0$. The ratio of the magnetic moment of the coils in the case of an equilateral triangle to that for a square is $1: \sqrt{y}$ where $y$ is________.
An iron rod of length I and magnetic moment M is bent in the form of a semicircle. Now the magnetic moment of this Iron rod is -
A charged particle going around in a circle can be considered to be a current loop. A particle of mass $m$ carrying charge $q$ is moving in a plane with speed $v$ under the influence of magnetic field $\vec{B}$. The magnetic moment of this moving particle:
JEE Main 2026: January Question Paper with Solutions
JEE Main 2026 Tools: College Predictor
JEE Main 2026: Important Formulas | Foreign Universities in India
A hollow metallic cone of semi-vertical angle $\theta$ and height $h$ is rotating about its axis at an angular velocity $\omega$ as shown. If it is given charge $Q$ is distributed uniformly then.
(radius of the base of the cone is R )
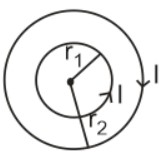
Two concentric circular loops of radii $\mathrm{r}_1=30 \mathrm{~cm}\ and\:\: \mathrm{r}_2=50 \mathrm{~cm}$ are placed in $\mathrm{X}-\mathrm{Y}$ plane as shown in the figure. A current $\mathrm{I}=7 \mathrm{~A}$ is flowing through them in the direction as shown in the figure. The net magnetic moment of this system of two circular loops is approximately:
Three identical bar magnets, each having a magnetic moment $M$, are placed in a straight line with their magnetic moments aligned in the same direction. What is the resultant magnetic moment of the system?
An iron rod of length land magnetic moment M is bent in the form of a semicircle. Now its magnetic moment will be:
Match List-I with List-II.
| List-I | List-II | ||
| A | Permeability of free space | I | $\left[\mathrm{M} \mathrm{L}^2 \mathrm{~T}^{-2}\right]$ |
| B | Magnetic field | II | $\left[\mathrm{M} \mathrm{L}^{-2} \mathrm{~T}^{-1}\right]$ |
| C | Magnetic moment | III | $\left[\mathrm{M} \mathrm{L} \mathrm{T}^{-2} \mathrm{~A}^{-2}\right]$ |
| D | Torsional constant | IV | $\left[\mathrm{L}^2 \mathrm{~A}\right]$ |
Choose the correct answer from the options given below:
If a magnet of magnetic moment M is divided into three parts of equal length then the magnetic moment of each part will become:
JEE Main 2026 College Predictor
Discover your college admission chances with the JEE Main 2026 College Predictor. Explore NITs, IIITs, CFTIs and other institutes based on your percentile, rank, and details.
Try NowConcepts Covered - 1
Magnetic dipole moment of a revolving electron
Magnetic dipole moment of a revolving electron-
Let us consider an electron that is revolving around in a circle of radius r with a velocity v . The charge of the electron is e and its mass is m , both of which are constant. The time period T of the electrons' orbit is -
$
T=\frac{\text { Circumference }}{\text { Velocity }}=\frac{2 \pi r}{v}
$
So the current due to motion of electron is -
$
i=\frac{q}{T}=\frac{-e}{\frac{2 \pi r}{v}}=\frac{-e v}{2 \pi r}
$
Now, as we know that the direction of current is opposite to the direction of motion of electron. Now the magnetic moment is defined as -
$
\mu=i A
$
So the Magnetic moment of an electron:
$
\begin{aligned}
\mu & =\frac{-e v}{2 \pi r} A=\frac{-e v}{2 \pi r} \pi r^2 \\
\mu & =\frac{-e r v}{2}
\end{aligned}
$
If we divide and multiply by the mass of the electron,
$
\mu=\frac{-e}{2 m_e} m_e v r
$
As we have studied that that the angular momentum $L$ is given by:
$
\mathrm{L}=\mathrm{mvr}
$
So the above equation can be written as -
$
\mu=\frac{-e}{2 m_e} L
$
The negative sign shows that the velocity and current are on opposite directions as shown in the figure given above. Also in the vector form it is written as -
$
\vec{\mu}=\frac{-e}{2 m_e} \vec{L}
$
Now, by Niels Bohr (we have studied this particular concept in Atomic structure of Chemistry and we will study this in detail in the chapter Atoms and Nuclei of Physics), Angular momentum of the electron is given as -
$
L=n \frac{h}{2 \pi}, n=0, \pm 1, \pm 2 \ldots
$
Where n is the orbit quantum number and h is the Planck's constant,
Now by using the equation (1)
$
\begin{aligned}
\mu & =n \frac{-e}{2 m_e} \frac{h}{2 \pi} \\
\mu & =-n \frac{e h}{4 \pi m_e}
\end{aligned}
$
If we put $\mathrm{n}=1$, then the equation become -
$
\mu_B=-\frac{e h}{4 \pi m_e}=9.27 \times 10^{-24} \mathrm{~J} / T \quad \text { (This is called Bohr Magneton } \mu_{\mathrm{B}}
$
Study it with Videos
"Stay in the loop. Receive exam news, study resources, and expert advice!"
Get Answer to all your questions
B.Tech/B.Arch Admissions OPEN
Amity University-Noida B.Tech Admissions 2026
ApplyAmong top 100 Universities Globally in the Times Higher Education (THE) Interdisciplinary Science Rankings 2026
Amrita University B.Tech 2026
ApplyApplication Deadline: 15th April | Recognized as Institute of Eminence by Govt. of India | NAAC ‘A++’ Grade | Upto 75% Scholarships
VIT Bhopal University | B.Arch Admissions 2026
ApplyMark presence in the Modern Architectural field with Bachelor of Architecture | Highest CTC : 70 LPA | Accepts NATA Score
VIT Bhopal University | Integrated M.Tech Admissions 2026
ApplyIntegrated M.Tech admissions open @ VIT Bhopal University | Highest CTC 70 LPA | Application Closing Soon | Apply now
MAHE, Manipal - B.Tech Admissions 2026
ApplyFinal Application Deadline: 23rd March | NAAC A++ Accredited | Accorded institution of Eminence by Govt. of India | NIRF Rank #3
Western India Inst of Aeronautics (WIIA) Admissions 2026
ApplyTop Recruiters: Qatar Airways, Air Asia, SpiceJet, Flydocs etc.