LC Oscillations - Practice Questions & MCQ

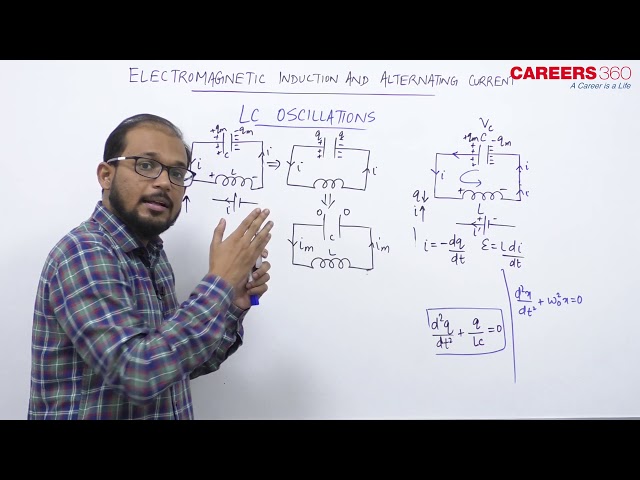
LC oscillations:

When a charged capacitor is allowed to discharge through a non-resistance, electrical oscillations of constant amplitude and frequency are produced. These oscillations are called LC-oscillations.

Let a capacitor be charged q_m (at t = 0) and connected to an inductor as shown in Fig.
The moment the circuit is completed, the charge on the capacitor starts decreasing, giving rise to the current in the circuit.

Let q and i be the charge and current in the circuit at time t.

Since $\frac{d i}{d t}$ is positive, the induced emf in $L$ will have polarity as shown, i.e., $v_b<v_a$.
According to Kirchhoff's loop rule,

$
\frac{q}{C}-L \frac{\mathrm{~d} i}{\mathrm{~d} t}=0
$

$\mathrm{i}=-(\mathrm{dq} / \mathrm{dt})$ in the present case (as q decreases, 1 increases).

$
\frac{\mathrm{d}^2 q}{\mathrm{~d} t^2}+\frac{1}{L C} q=0
$

This equation has the form for

$
\frac{\mathrm{d}^2 x}{\mathrm{~d} t^2}+\omega_0^2 x=0
$

a simple harmonic oscillator. The charge, therefore, oscillates with a natural frequency.

$
\omega_0=\frac{1}{\sqrt{L C}}
$

And varies sinusoidally with time as:

$
q=q_m \cos \left(\omega_0 t+\phi\right)
$

where $q_m$ is the maximum value of $q$ and $\varphi$ is a phase constant. Since $q=q_m$ at $t=0$, we have $\cos \phi=1$ or $\phi=0$. Therefore, in the present case

$
q=q_m \cos \left(\omega_0 t\right)
$

The current $\mathrm{i}\left(=\frac{d i}{d t}\right.$ ) is given by

$
i=i_m \sin \left(\omega_0 t\right)
$

where $i_m=\omega_0 q_m$
Since there is no current in the circuit; energy in the inductor is zero. Thus, the total energy of $L C$ circuit is

$
U=U_E=\frac{1}{2} \frac{q_m^2}{C}
$