Standing Wave On A String - Practice Questions & MCQ

Standing waves

When two sets of progressive wave of same type (both longitudinal or both transverse) having the same amplitude and same time period or frequency or wavelength travelling along the same straight line with same speed in opposite directions superimpose, a new set of waves are formed. These are called stationary waves.

Some of the characteristics of standing waves :

(1) In this the disturbance is confined to a particular region between the starting point and reflecting point of the wave.
(2) In this there is no forward motion of the disturbance from one particle to the adjoining particle and so on, beyond this particular region.
(3) The total energy in a stationary waves is twice the energy of each of incident and reflected wave. But there is no flow or transfer of energy along the stationary wave.
(4) Points in a standing wave, which are permanently at rest. These are called nodes. The distance between two consecutive nodes is $\frac{\lambda}{2}$

(5) The Points on the standing wave having maximum amplitude is known as antinodes. The distance between two consecutive antinodes is also $\frac{\lambda}{2}$
(6) All the particles execute simple harmonic motion about their mean position (except those are at nodes) with the same time period.

Note - In standing waves, if the amplitude of component waves are not equal. Resultant amplitude at nodes will not be zero. It will be minimum . Because of this, some energy will pass across nodes and waves will be partially standing.

Let us take an example to understand and derive equation of standing wave - 

Let us take a string and when a string is under tension and set into vibration, transverse harmonic waves propagate along its length. If the length of string is fixed, reflected waves will also exist. These incident and reflected waves will superimpose to produce transverse stationary waves in a string

Incident wave $y_1=a \sin \frac{2 \pi}{\lambda}(v t+x)$
Reflected wave $y_2=a \sin \frac{2 \pi}{\lambda}[(v t-x)+\pi]=-a \sin \frac{2 \pi}{\lambda}(v t-x)$
Now we can apply principle of superposition on this and get -

$
y=y_1+y_2=2 a \cos \frac{2 \pi v t}{\lambda} \sin \frac{2 \pi x}{\lambda}
$

So, $y=(2 A \sin k x) \cos \omega t$
So, it can be written as - $y=R \cos \omega t$
where, $R=2 A \operatorname{sink} x$.
Equation (1) and (2) shows that after superposition of the two waves the medium particle execute SHM with same frequency and amplitude. Thus on superposition of two waves travelling in opposite direction, the resulting interference pattern will form Stationary waves.

Nodes and antinodes -
Points in a standing wave, which are permanently at rest. These are called nodes. The Points on the standing wave having maximum amplitude is known as antinodes.

For nodes -
From equation (2) we can say that $-k x=n \pi$

$
x=\frac{n \pi}{k}=\frac{n \pi}{\frac{2 \pi}{\lambda}}=\frac{n \lambda}{2}
$

So,

$
x=0, \frac{\lambda}{2}, \lambda
$

So, at point where

For antinodes - 

From equation (2) we can say that

$
k x=(2 n+1) \frac{\pi}{2}
$

So,

$
x=(2 n+1) \frac{\lambda}{4}
$

So, again using equation

$
y= \pm 2 A
$

Thus at point for which $x=\frac{\lambda}{4}, \frac{3 \lambda}{4}, \frac{5 \lambda}{4} \ldots . .$, displacemnet is maximum $( \pm 2 A)$

Standing wave in a string fixed at both ends - 

As we know that a string is said to vibrate if it vibrate according to the given equation - 

$
y=(2 A \sin k x) \cos \omega t
$

From this equation, for a point to be node,

$
x=\frac{n \lambda}{2}, \text { where } n=0,1,2,3, \ldots
$

In this the string is fixed at both the ends, so these ends are node. So, for $x=0$ and for $x=L_{\text {(which will }}$ be node). So, it can be written as -

$
L=\frac{n \lambda}{2}, \text { or, } \lambda=\frac{2 L}{n} \text { where } n=1,2,3, \ldots
$

So, corresponding frequencies will be $=$

$
f=\frac{v}{\lambda}=n\left(\frac{v}{2 L}\right), \text { where } n=1,2,3 \ldots
$
 

here,  = speed of travelling waves on the string

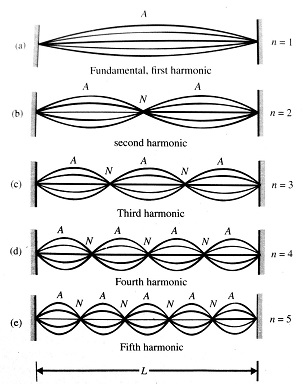
In the above figure we can see that by putting the values of ' $n$ ', we are getting different frequencies. For example -
1. for $n=1, f=\frac{v}{2 L}$ and it is called fundamental frequency or first harmonic

The corresponding mode is called fundamental mode of vibration.
2. If $n=2, f_1=2\left(\frac{v}{2 L}\right)=\frac{v}{L}$

This second harmonic or first overtone and $f_1=2 f$

Similar to this, we can increase the value of ' $n$ ' and we get the respective harmonic and overtone.

Now, the velocity of wave in string is given by-

$
\nu=\sqrt{\frac{T}{\mu}}
$

So the natural frequency can be written as -

$
f_n=\frac{n}{2 L} \sqrt{\frac{T}{\mu}} ; n=1,2,3, \ldots
$
 

Standing wave in a string fixed at one end - 

In this case, one end is fixed and the other end is free. In the fundamental mode, the free end is an antinode, the length of string 

                                                                                 $L=\frac{\lambda}{4}$

So, in the next mode-

$
L=\frac{3 \lambda}{4}
$

So, in general we can write the equation =

$
L=\frac{n \lambda}{4}, n=1,3,5 \ldots
$
 

From this we can write the resonance frequency -

$
f_n=n \frac{v}{4 L}=n f_1 ; n=1,3,5, \ldots
$

where, $f_1=\frac{v}{4 L} \quad$ (Fundamental frequency)