Sonometer - Practice Questions & MCQ

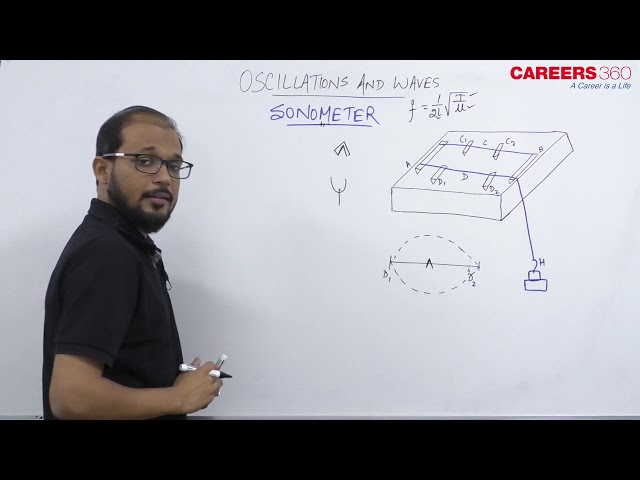
Sonometer - 

It is a device used to measure the velocity of the transverse mechanical wave in a stretched metal wire.

The principle of sonometer is based on the resonance of string vibrations. Working oscillations are induced in a clamped string by an external source like a tuning fork or an oscillator and because of this, the amplitude becomes very high when resonance takes place. 

There are two figures given below which show the setup of the Sonometer. There is a wooden box M on which wire $A B$ is stretched by weight as shown in figure (a). There are two clamps $C_1$ and $C_2$ which are ready to slide to change the length of the wire between the clamps.

Now we are placing an oscillating tuning fork in contact with the sonometer wire (See figure (b)). When they get in touch, some oscillations are transferred to the wire. Let the tension in the wire is T and $\mu$ is the mass per unit length of the wire. Also $n_0$ is the frequency of tuning fork, then the wavelength of the wave in the wire is -

$
\lambda=\frac{v}{n_0}=\frac{1}{n_0} \sqrt{\frac{T}{\mu}}
$
 

If the length between clamps is an integral multiple of $\lambda / 2$ then stationary waves are established in the portion of wire between $C_{1 \text { and }} C_2$. To do this, Clamp $C_1$ is fixed and $C_2$ is displaced so that the oscillation amplitude of wire is increasing and stationary waves are established. Let in this situation the length between clamps be $l$, now again $C_2$ is displaced away from $C_1$ so that again resonance is obtained. This will happen again when the clamp reaches the position $C_3$ and when the next node of stationary waves is present. Let this length be $l$, if $l_1$ and $l_2$ are two successive resonance lengths then we can write -

$
\begin{gathered}
l_2-l_1=\frac{\lambda}{2} \\
\text { So, }^\lambda=2\left(l_2-l_1\right)
\end{gathered}
$

If $n_0$ is the frequency of oscillation, then the velocity of the string wave in wire -

$
\begin{aligned}
v & =n_0 \lambda \\
& =2 n_0\left(l_2-l_1\right)
\end{aligned}
$

This is partial measured velocity and we can compare this velocity with the formula $\sqrt{\frac{T}{\mu}}$