Potential Energy Of A Dipole In An Electric Field - Practice Questions & MCQ

When a dipole is kept in a uniform electric field. The net force experienced by the dipole is zero as shown in the below figure.

I.e Fnet = 0

But it will experience torque. And Net torque about the center of dipole is given as

$\tau=Q E d \sin \theta$ or $\tau=P E \sin \theta$ or $\vec{\tau}=\vec{P} \times \vec{E}$

Work done in rotation-

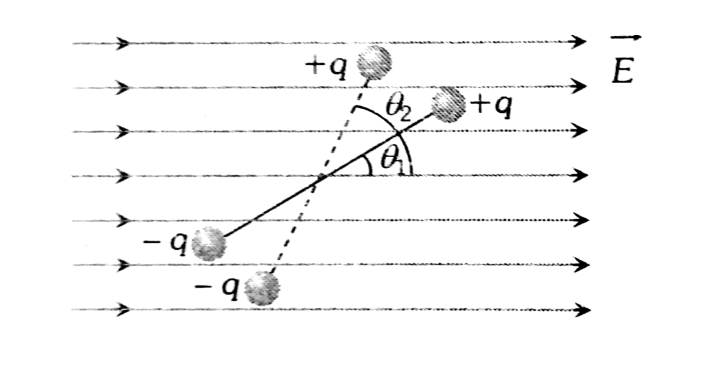
Then work done by electric force for rotating a dipole through an angle $\theta_2$ from the equilibrium position of an angle $\theta_1$ (As shown in the above figure) is given as

$
\begin{aligned}
& W_{e l e}=\int \tau d \theta=\int_{\theta_1}^{\theta_2} \tau d \theta \cos \left(180^0\right)=-\int_{\theta_1}^{\theta_2} \tau d \theta \\
& \Rightarrow W_{e l e}=-\int_{\theta_1}^{\theta_2}(P \times E) d \theta=-\int_{\theta_1}^{\theta_2}(P E \operatorname{Sin} \theta) d \theta=P E\left(\cos \Theta_2-\cos \Theta_1\right)
\end{aligned}
$

And So work done by an external force is $W=P E\left(\cos \Theta_1-\cos \Theta_2\right)$
For example

$
\begin{gathered}
\text { if } \Theta_1=0^{\circ} \text { and } \Theta_2=\Theta \\
W=P E(1-\cos \Theta) \\
\text { if } \Theta_1=90^{\circ} \text { and } \Theta_2=\Theta \\
W=-P E \cos \Theta
\end{gathered}
$

Potential Energy of a dipole kept in Electric field-
As $\Delta U=-W_{e l e}=W$
So change in Potential Energy of a dipole when it is rotated through an angle $\theta_2$ from the equilibrium position of an angle $\theta_1$ is given as $\Delta U=P E\left(\cos \Theta_1-\cos \Theta_2\right)$

$
\begin{aligned}
& \text { if } \Theta_1=90^{\circ} \text { and } \Theta_2=\Theta \\
& \Delta U=U_{\theta_2}-U_{\theta_1}=U_\theta-U_{90}=-P E \cos \Theta
\end{aligned}
$

Assuming $\Theta_1=90^{\circ}$ and $U_{90^{\circ}}=0$
we can write $U=U_\theta=-\vec{P} \cdot \vec{E}$

Equilibrium of Dipole-

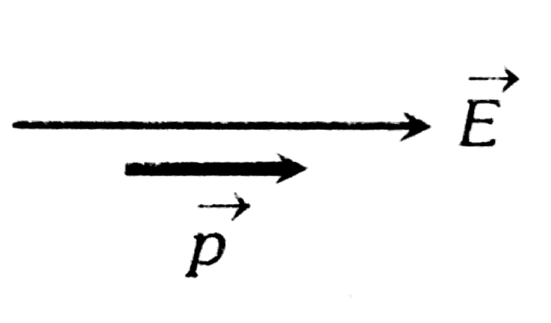
1. Stable Equilibrium-

$
\begin{aligned}
& \Theta=0^{\circ} \\
& \tau=0 \\
& U_{\min }=-P E
\end{aligned}
$
 

2. Unstable Equilibrium-

$\begin{aligned} & \Theta=180^{\circ} \\ & \tau=0 \\ & U_{\max }=P E\end{aligned}$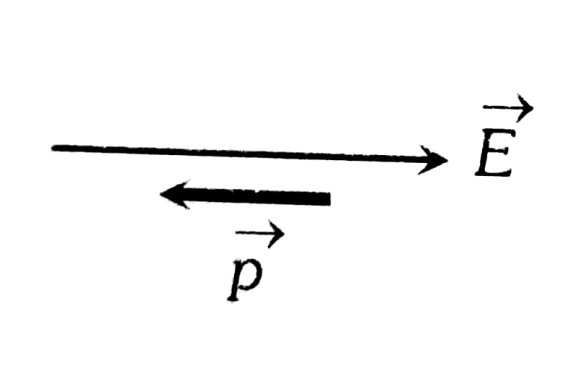

Note-

When $\Theta=90^{\circ}$
then $\tau_{\text {max }}=P E$ and $U=0$
and it is important to note here that dipole is not in equilibrium since $\tau_{\max } \neq 0$