Interference And Principle Of Superposition - Practice Questions & MCQ

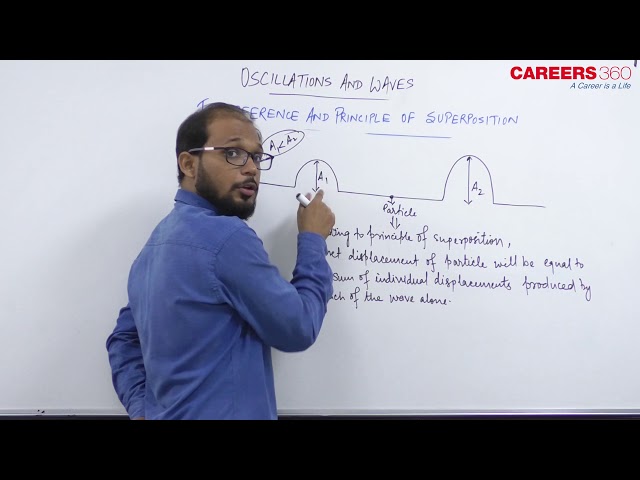
When two waves of same frequency, the same wavelength, same velocity (nearly equal amplitude) moves in the same direction, Their superimposition results in the interference. Due to interference, the resultant intensity of sound at that point is different from the sum of intensities due to each wave separately. This modification of intensity due to the superposition of two or more waves is called interference.

The displacement at any time due to any number of waves meeting simultaneously at a point in a medium is the vector sum of the individual displacements due to each one of the waves at that point at the same time.

if $y_1, y_2, y_3 \cdots \cdots$ are the displacements at a particular time at a particular position, due to individual waves, then the resultant displacement would be :

$
y=y_1+y_2+y_3 \ldots \ldots
$
 

Let at a given point two waves arrive with the phase difference $\phi$ and the equation of these waves are given by $y_1=a_1 \sin (\omega t), y_2=a_2 \sin (\omega t+\phi)$ then by principle of superposition

$
y=y_1+y_2 \Longrightarrow A \sin (\omega t+\theta)
$

Where

$
A=\sqrt{a_1^2+a_2^2+2 a_1 a_2 \cos (\phi)} \quad \text { and } \tan (\theta)=\frac{a_2 \sin \phi}{a_1+a_2 \cos (\phi)}
$