Gravitational Potential - Practice Questions & MCQ

In a gravitational field potential V at a point, P is defined as negative of work done per unit mass in changing the position of a test mass from some reference point to the given point.

Note-usually reference point is taken as infinity and potential at infinity is taken as Zero.

We know that

$
W=\int \vec{F} \cdot \overrightarrow{d r}
$

So $V=-\frac{W}{m}=-\int \frac{\vec{F} \cdot \overrightarrow{d r}}{m}$
And $\vec{I}=\frac{\vec{F}}{m}$

$
V=-\int \vec{I} \cdot \overrightarrow{d r}
$

$V \rightarrow$ Gravitational potential
$I \rightarrow$ Field Intensity
$d r \rightarrow$ small distance
We can also write

$
I=-\frac{d V}{d r}
$

Means a negative gradient of potential gives the intensity of the field.
The negative sign indicates that in the direction of intensity the potential decreases.
- It is a scalar quantity.
. Unit $\rightarrow$ Joule $/ \mathrm{kg}$ or $\mathrm{m}^2 / \mathrm{sec}^2$
- Dimension : $\left[M^0 L^2 T^{-2}\right]$

• Gravitational Potential at a distance 'r'

If the field is produced by a point mass then 

$
\begin{aligned}
& I=\frac{G M}{r^2} \\
& V=-\int \vec{I} \cdot \overrightarrow{d r} \\
& \text { So } \\
& V=-\frac{G M}{r}
\end{aligned}
$

at $r=\infty \quad V=0=V_{\max }$

 

• Gravitational Potential difference

In the gravitational field, the work done to move a unit mass from one position to the other is known as Gravitational Potential difference.

            If the point mass M is producing the field

Point A and B are shown in the figure.

=Gravitational potential at point A

=Gravitational potential at point B

 

    

 

             

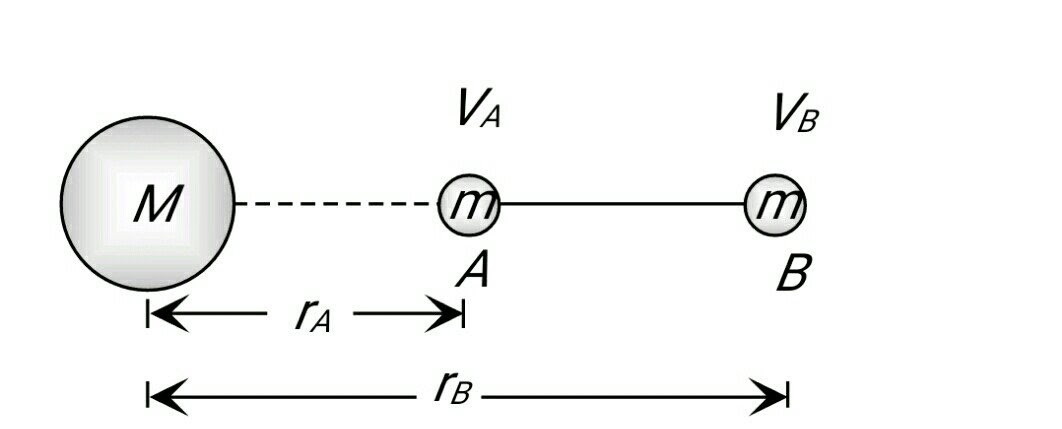
$r_B \rightarrow$ the distance of mass at $B$
$r_A \rightarrow$ distance of mass at $A$
$\Delta V=$ The gravitational potential difference in bringing unit mass m from point A to point B in the gravitational field produced by $M$.

$
\begin{aligned}
& \Delta V=V_B-V_A=\frac{W_{A \rightarrow B}}{m} \\
& \Delta V=-G M\left[\frac{1}{r_B}-\frac{1}{r_A}\right]
\end{aligned}
$
 

 

• Superposition of Gravitational potential

The net gravitational potential at a given point due to different point masses (M₁,M₂,M₃…) can be calculated  by doing a scalar sum of their individuals Gravitational potential.

   $\begin{aligned} V & =V_1+V_2+V_3 \cdots \\ & =-\frac{G M_1}{r_1}-\frac{G M_2}{r_2}-\frac{G M_3}{r_3} \cdots \\ V & =-G \sum_{i=1}^{i=n} \frac{M_i}{r_i} \\ M_i & \rightarrow \text { mass } \\ r_i & \rightarrow \text { distances }\end{aligned}$

 

• Point of zero potential

           Let m₁ and m₂ are separated at a distance d from each other

 

          

And P is the point where net Gravitational potential $V=V_1+V_2=0$
Then P is the point of zero Gravitational potential
Let point $P$ is at distance $x$ from $m_1$
Then For point $P$

$
\begin{aligned}
& V=V_1+V_2=0 \\
& -\frac{G m_1}{r_1}-\frac{G m_2}{r_2}=0 \\
& -\frac{G m_1}{x}-\frac{G m_2}{d-x}=0 \\
& \quad x=\frac{m_1 d}{m_1-m_2}
\end{aligned}
$
 

For Uniform circular ring

$r=$ distance from ring
$a \rightarrow$ radius of Ring
$V \rightarrow$ Potential

At a point on its Axis

$
V=-\frac{G M}{\sqrt{a^2+r^2}}
$

At the center

$
V=-\frac{G M}{a}
$
 

For Uniform disc

 

$a \rightarrow$ Radius of disc

M-mass of disc
- At the center of the disc

$
V=-\frac{2 G M}{a}
$

- At a point on its axis

$
V=-\frac{2 G M}{a^2}\left(\sqrt{a^2+x^2}-x\right)
$
 

 For Spherical shell

 

$R \rightarrow$ Radius of shell
$r \rightarrow$ distance from the center of the shell
- Inside the surface

$
\begin{aligned}
r & <R \\
V & =-\frac{G M}{R}
\end{aligned}
$

- on the surface

$
\begin{aligned}
r & =R \\
V & =-\frac{G M}{R}
\end{aligned}
$

- Outside the surface

$
\begin{aligned}
r & >R \\
V & =-\frac{G M}{r}
\end{aligned}
$
 

 

Uniform solid sphere

$R \rightarrow$ Radius of sphere
$M \rightarrow$ Mass of sphere
$r \rightarrow$ distance from the center of sphere
- Inside the surface

$
\begin{aligned}
r & <R \\
V & =-\frac{G M}{2 R}\left[3-\left(\frac{r}{R}\right)^2\right]
\end{aligned}
$

- on the surface

$
V_{\text {surface }}=-\frac{G M}{R}
$

- Outside the surface

$
V=-\frac{G M}{r}
$

- Tip-

$
\text { V centre }=\frac{3}{2} V \text { sur face }
$