Careers360 Logo
Engineering and Architecture
Search Colleges, Exams, Schools & more
JEE Main Eligibility Criteria 2025- Marks in 12th, Age Limit, Number of Attempts
  1. Home
  2. JEE Main
  3. Study Material
  4. Electric Potential - Practice Questions & MCQ

Electric Potential - Practice Questions & MCQ

Edited By admin | Updated on Sep 18, 2023 18:34 AM | #JEE Main

Quick Facts

  • Electric potential is considered one of the most asked concept.

  • 48 Questions around this concept.

Solve by difficulty

QuestionEASY

Two thin wire rings each having a radius R are placed at a distance d  apart with their axes coinciding. The charges on the two rings are +Q and -Q  The potential difference between the centers of the two rings is

View Solution

An electric charge 10^{-3}\mu C  is placed at the origin (0,0)of  X-Y co-ordinate system . Two points A and B are situated at \left ( \sqrt{2},\sqrt{2} \right )\: and\: \left ( 2,0 \right ) respectively. The potential difference between the point  A and B will be

View Solution

A charge Q is uniformly distributed over a long rod AB of length L, as shown in the figure. The electric potential at the point O lying at a distance L from the end A is :

 

View Solution

Two points P\; and\; Q are maintained at the potentials of 10 V and -4 V respectively. The work done in moving 100 electrons from P\; to\; Q  is

View Solution

This question contains Statement-1 and Statement-2. Of the four choices given after the statements, choose the one that best describes the two statements.

Statement-1:  For a charged particle moving from point P to point Q , the net work done by an electrostatic field on the particle is independent of the path connecting point P to point Q.

Statement-2:  The net work done by a conservative force on an object moving along a closed loop is zero.

 

View Solution

Concepts Covered - 1

Electric potential

In an Electric field Electric potential V at a point, P is defined as work done per unit charge in changing the position of test charge from some reference point to the given point.

Note-usually reference point is taken as infinity and potential at infinity is taken as Zero.

We know that W_{ext} =\int {\overrightarrow{F_{ext}}\cdot \overrightarrow{dr}}

Since

W_{ext}=\Delta U \ \ and \ \ \Delta {KE}=0 \\ \Rightarrow \text{For all time }\ \ F_{net}=0 \\ \Rightarrow \overrightarrow{F}_{ext} +\overrightarrow{F}_{system}=0

i.e  \overrightarrow{F}_{ext} = -\overrightarrow{F}_{system}     
  

So V=\frac{W_{ext}}{q_0}=\int \frac{\overrightarrow{F}_{ext}\cdot \overrightarrow{dr}}{q_0}=-\int \frac{\overrightarrow{F}_{system}\cdot \overrightarrow{dr}}{q_0}

where

V\rightarrow Electric potential

  •  It is a scalar quantity.

  •  SI \ \ Unit \to \;\frac{J}{C}=volt while  CGS unit is stat volt  

           1 \ volt=\frac{1}{300} \ stat \ volt.   

  • Dimension -   \begin{aligned}[V]=\left[\frac{W}{q_{0}}\right] &=\left[\frac{M L^{2} T^{-2}}{A T}\right]=\left[M L^{2} T^{-3} A^{-1}\right] \end{aligned}.

   

  • Electric Potential at a distance 'r'

            If the Electric field is produced by a point charge q then 

F= \frac{Kqq_0}{r^{2}}

Using V=\frac{W_{ext}}{q_0}=\int \frac{\overrightarrow{F}_{ext}\cdot \overrightarrow{dr}}{q_0}=-\int \frac{\overrightarrow{F}_{system}\cdot \overrightarrow{dr}}{q_0}

          V=\frac{Kq}{r}

                at r=\infty       V=0=V_{max}

  • Electric Potential difference

In the Electric field, the work done to move a unit charge from one position to the other is known as Electric Potential difference.

If the point charge Q is producing the field

Point A and B are shown in the figure.

V_{A}=Electric potential at point A

V_{B}=Electric potential at point B

   

 

                   r_{B}\rightarrow the distance of charge at B

                  r_{A}\rightarrow distance of charge at A

             \Delta V=The Electric potential difference in bringing charge q from point A to point B in the Electric field produced by Q.

            \Delta V=V_{B}-V_{A}=\frac{W_{A\rightarrow B}}{q}

           \Delta V=KQ\left [ \frac{1}{r_{B}}-\frac{1}{r_{A}} \right ]

  • Superposition of Electric potential

Statement- Total electric potential at a given point in space due to all the charges placed around it is the scalar or algebraic addition of electric potential due to individual charges at that point.

i.e

The net Electric potential at a given point due to different point masses (Q1,Q2,Q3…) can be calculated by doing a scalar sum of their individuals Electric potential.

 V=V_{1}+V_{2}+V_{3}+\cdots=\frac{kQ_{1}}{r_{1}}+k\frac{Q_{2}}{r_{2}}+\frac{k\left ( Q_{3} \right )}{r_{3}}+\cdots=\frac{1}{4 \pi \varepsilon_{0}} \sum \frac{Q_{i}}{r_{i}}

        

 

  • Electric Potential due to Continuous charge distribution

                  \dpi{100} V=\int dV=\int \frac{dq}{4\pi \varepsilon _{0}r}

  • Graphical representation

     As we move on the line joining two charges then the variation of Potential with distance is given below.

    

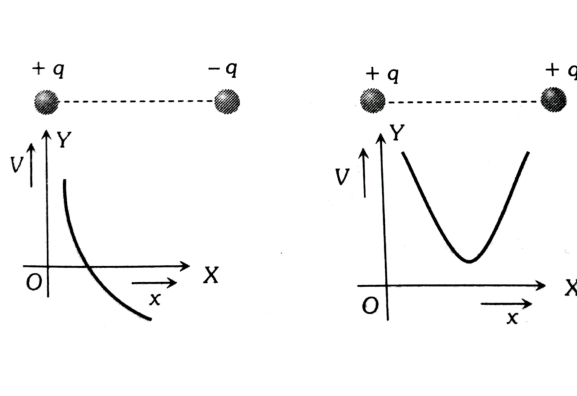
  • Zero potential due to a system of a two-point charge

1.For internal point

 \left ( It \: is \: assumed\: that\left | Q_{1} \right |< \left | Q_{2} \right | \right )

Let at P, V is zero

 \\*V_P=0\Rightarrow \: \: \frac{Q_{1}}{x_{1}}= \frac{Q_{2}}{\left ( x-x_{1} \right )} \\* \Rightarrow x_{1}= \frac{x}{\left ( Q_{2}/Q_{1}+1 \right )}

 

If both charges are like then the resultant potential is not zero at any finite point.

2.For external point

Let at P, V is zero

\\*V_ P\Rightarrow \frac{Q_{1}}{x_{1}}= \frac{Q_{2}}{\left ( x+x_{1} \right )}\\* \Rightarrow x_{1}= \frac{x}{\left ( Q_{2}/Q_{1}-1 \right )}          

Study it with Videos

Electric potential

Study other Related Concepts

Electric Potential Current Topic

Electric Charge
Electric Charge And Electrification
Coulomb's Law
Electric Field
Electric Field Lines
Electric Field Intensity: Continuous Charge Distribution
Electric Field Due To A Uniformly Charged Ring
Electric Field Of Charged Disk
Electric Field Due To An Infinitely Long Charged Wire
Motion of charged particle in uniform electric field

"Stay in the loop. Receive exam news, study resources, and expert advice!"

Get Answer to all your questions

JEE Main Articles

JEE Main Syllabus 2025 PDF (Physics, Chemistry, Maths)
Oct 17, 2024
JEE Main Exam Date 2025 - NTA JEE Mains Session 1 & 2 Exam Schedule
Oct 17, 2024
JEE Main Registration 2025 Session 1, 2 - IIT Application Form Date, Fees, Documents Required
Oct 17, 2024
JEE Main Exam Pattern 2025 (Revised) - Total Marks in JEE Mains, Paper Pattern, Marking Scheme
Oct 17, 2024
JEE Main 2025 - Exam Pattern (Revised), Dates, Registration, Preparation Tips, Previous Year Papers
Oct 17, 2024
How to Prepare for JEE Main 2025?- Study Plan
Oct 17, 2024
JCECE Application Form 2024, Registration (Closed) - Apply Online here
Oct 17, 2024
JEE Main Login 2025 - Candidate Login for Registration, Result, Answer Key
Oct 16, 2024

B.Tech/B.Arch Admissions OPEN

UPES B.Tech Admissions 2025
UPES B.Tech Admissions 2025
Apply

Ranked #46 among universities in India by NIRF | Highest CTC 50 LPA | 100% Placements

Amity University, Noida B.Tech Admissions 2024
Amity University, Noida B.Tech Admissions 2024
Apply

Asia's Only University with the Highest US & UK Accreditation

JSS University Noida Admissions 2024
JSS University Noida Admissions 2024
Apply

170+ Recruiters Including Samsung, Zomato, LG, Adobe and many more | Highest CTC 47 LPA

Atlas SkillTech University | B.Tech Admissions
Atlas SkillTech University | B.Tech Admissions
Apply

Hands on Mentoring and Code Coaching | Cutting Edge Curriculum with Real World Application

Parul University B.Tech Admissions 2025
Parul University B.Tech Admissions 2025
Apply

India's youngest NAAC A++ accredited University | NIRF rank band 151-200 | 2200 Recruiters | 45.98 Lakhs Highest Package

Vidyashilp University B.Tech Admissions 2025
Vidyashilp University B.Tech Admissions 2025
Apply

Avail upto 100% Scholarships

View All Application Forms
News and Notifications
September 19, 2024 - 12:45 PM IST :
September 19, 2024 - 12:43 PM IST :
JEE Main 2025: NTA scraps optional questions in section B introduced during COVID pandemic
October 17, 2024 - 10:33 PM IST
How to prepare for JEE Main 2025 in 3 months? Study plan, important topics
October 17, 2024 - 05:18 PM IST
NTA Exam Calendar 2025 Live: JEE Main, NEET, CUET schedule to be announced soon; download at nta.ac.in
October 15, 2024 - 10:25 PM IST
NTA Exam Calendar 2025: JEE Main, NEET, CUET exam dates soon
October 15, 2024 - 07:24 AM IST
JEE Main, NEET, CUET 2025 Dates Live: NTA to announce exam calendar soon on nta.ac.in; latest updates
October 14, 2024 - 07:26 AM IST
NTA Exam Calendar 2025 Live: JEE Main, NEET, CUET, tentative schedule soon at nta.ac.in; how to download
October 12, 2024 - 09:40 PM IST
JEE Main, NEET, CUET UG 2025 Dates Live: NTA exam calendar soon for BTech, MBBS, UG admissions
October 12, 2024 - 10:09 AM IST

Download Careers360 App's

Regular exam updates, QnA, Predictors, College Applications & E-books now on your Mobile

  • student
    300M+

    Students

  • colleges
    36,000+

    Colleges

  • exams
    550+

    Exams

  • ebook
    1500+

    E-Books

  • certification
    16000+

    Certifications

student
Mobile Screen

We Appeared in

Joint Entrance Examination (Main)      
JEE Main 2025 Sample Papers
Back to top