Displacement Current - Practice Questions & MCQ

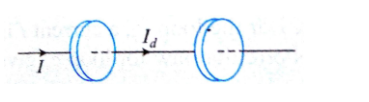
Displacement current-

It is a current which produces in the region in which the electric field and hence the electric flux changes with time. As we know that an electrical current produces a magnetic field around it. So if there is a change in an electric field, the magnetic field will be produced. This effect explains the existence of radio waves, gamma rays and visible light, as well as all other forms of electromagnetic waves. So it is very important to effect and let us understand this effect with the help of Ampere’s circuital law which is given by - 

                                                                           $
\oint \mathbf{B} \cdot \mathrm{d} \mathbf{l}=\mu_0 i(t)
$

The below figure shows a parallel plate capacitor C which is a part of the circuit through which time-dependent current i(t) flows. Now we have to find the magnetic field at a point such as P, in a region outside the parallel plate capacitor. Now for applying Ampere’s circuital law we have to consider a plane circular loop of radius 'r' whose plane is perpendicular to the direction of the current-carrying wire, and we can see that it is centred symmetrically with respect to the wire. As we can see that from symmetry that the direction of the magnetic field is along the circumference of the circular loop and is the same in magnitude at all points on the loop so that B can be taken outside of the integration and by integrating the loop length, the left side of equation (1) will be equal to B(2π r). So we have

                                                                                  $B(2 \pi r)=\mu_0 i(t)$

Now we are going to change the surface taken for the Ampere's circuital law such that it has same boundary. Let us take two cases, which is shown in the below figure - 

                                                      (a)                                                                                    (b)

We can see from both the cases that both the surface nowhere touches the current. In case (a), it is pot like surface such that its base is between the plates and its mouth is having the same surface as we have taken in the earlier case. Similarly the case (b) is a tiffin like structure. Now if we apply the Ampere's circuital law again for both the cases, the left side of equation (1) will remain same but the right side will become zero because there is no current passes through the surface. But for the same surface and by same law we are getting different value of magnetic field which shows that something is incorrect or some term is missing. Now, what is that missing term?? If we take the case (b) again, we can see that an electric field will pass through the surface S. The magnitude of this electric field is equal to (Studied in the chapter on Electrostatics)- 

$
\frac{1}{\varepsilon_0} \frac{Q}{A}
$

Since the electric field is same over the area and zero outside the plate. So the electric flux will be equal to (By Gauss's Law) -

$
\Phi_{\mathrm{E}}=|\mathrm{E}| A=\frac{1}{\varepsilon_0} \frac{Q}{A} A=\frac{Q}{\varepsilon_0}
$

But if the charge changes with time, the equation can be written as -

$
\begin{aligned}
\frac{\mathrm{d} \phi_E}{\mathrm{~d} t} & =\frac{\mathrm{d}}{\mathrm{~d} t}\left(\frac{\mathcal{Q}}{\varepsilon_0}\right)=\frac{1}{\varepsilon_0} \frac{\mathrm{~d} Q}{\mathrm{~d} t} \\
& \Rightarrow \varepsilon_0\left(\frac{\mathrm{~d} \Phi_E}{\mathrm{~d} t}\right)=i
\end{aligned}
$
 

This is the missing term in Ampere’s circuital law. Now, if we add the total current carried by conductors through the surface, another term which is ε_o times the rate of change of electric flux through the same surface, the total has the same value of current 'i' for all surfaces.After doing this B at the point P is non-zero and becomes equal for all the cases, no matter which surface is used for calculating it. The current carried by conductors due to the flow of charges is called conduction current. The current, given by equation (2), is a new term, and is due to changing electric field. It is, therefore, called displacement current or Maxwell’s displacement current. Maxwell generalised the above consequences as following.

The source of a magnetic field is not just the conduction electric current due to flowing charges, but also the time rate of change of electric field. So we can write that - 

                                                                         $i=i_e+i_d=i_c+\varepsilon_0 \frac{d \Phi_E}{d t}$

where i_c and i_d is the coduction current and displacement current respectively.

This means that outside the capacitor plates, we have only conduction current i_c = i, and no displacement current, i.e., i_d = 0. On the other hand, inside the capacitor, there is no conduction current, i.e., i_c = 0, and there is only displacement current, so that i_d = i.

So, in general, the Ampere’s circuital law will be like - 

                                                                     $\oint \mathbf{B} \cdot \mathrm{d} \mathbf{l}=\mu_0 \boldsymbol{i}_e+\mu_0 \varepsilon_0 \frac{\mathrm{~d} \phi_E}{\mathrm{~d} t}$

                                                                     This is called Ampere-Maxwell law.