Davisson-germer Experiment - Practice Questions & MCQ

IIIT Hyderabad B.Tech Merit List 2024 - Check Toppers, Category Wise List

Quick Facts

Davisson-Germer Experiment is considered one of the most asked concept.
1 Questions around this concept.

Solve by difficulty

Match List - I (Fundamental Experiment) with List - II (its conclusion) and select the correct option from the choices given below the list :

(A) - (i) (B) - (iv) (C) - (iii)

(A) - (ii) (B) - (iv) (C) - (iii)

(A) - (ii) (B) - (i) (C) - (iii)

(A) -(iv) (B) - (iii) (C) - (ii)

View Solution

Concepts Covered - 0

Davisson-Germer Experiment

Davisson and Germer Experiment, for the first time, proved the wave nature of electrons through electron diffraction and also verified the de Broglie equation.

In this experiment, we will study the scattering of electrons by a Ni crystal.

The experimental setup for the Davisson and Germer experiment is enclosed within a vacuum chamber.

The experimental arrangement of the Davisson Germer experiment consists of the following main parts

Electron gun: An electron gun comprising of a tungsten filament F was coated with barium oxide and heated through a low voltage power supply. It emits electrons when heated to a particular temperature. The electrons emitted by the electron gun are again accelerated to a particular velocity.
Collimator: The accelerator is enclosed within a cylinder perforated with fine holes along its axis, these emitted electrons were made to pass through it. Its function is to render a narrow and straight (collimated) beam of electrons ready for acceleration.
Target: The target is a Nickel crystal. The beam produced from the cylinder is again made to fall on the surface of a nickel crystal. The crystal is placed such that it can be rotated about a fixed axis. Due to this, the electrons scatter in various directions.
Detector: A detector is used to capture the scattered electrons from the Ni crystal. The beam of electrons produced has a certain amount of intensity which is measured by the electron detector and after it is connected to a sensitive galvanometer, it is then moved on a circular scale to record the current.

Observations of Davisson Germer experiment-

The intensity of the scattered electron beam is measured for different values of angle of scattering ( $\phi$ ) by changing the $\phi$ (angle between the incident and the scattered electron beams).

These electrons formed a diffraction pattern. Thus the dual nature of matter was verified.

The energy of the incident beam of electrons can be varied by changing the applied voltage to the electron gun.

Note-Intensity of a scattered beam of electrons is found to be maximum when the angle of scattering is $50^{o}$ and the accelerating potential is 54 V.

i.e we could see a strong peak in the intensity. This peak was the result of the constructive interference of the scattered electrons.

The intensity of the scattered electrons is not continuous. It shows a maximum and a minimum value corresponding to the maxima and the minima of a diffraction pattern produced by X-rays.

Galvanometer in Davisson Germer Experiment-

The detector is connected to a sensitive galvanometer to measure the small values of current due to scattered beam of electrons.

Bragg’s formula-

The path difference between electrons scattered from adjacent crystal planes is given by $\Delta x=2dsin\theta$

and For constructive interference between the two scattered beams

$\Delta x=2d\sin \Theta = n\lambda$

where $d-distance\: between \: diffracting\: planes$

and $\theta$ is the angle between the incident rays and the surface of the crystal

For the above figure $\phi =scattering \ angle$

As $\theta+\phi+\theta=180^{o}$

So $\Theta = \frac{180-\phi }{2}$

As Intensity of a scattered beam of electrons is found to be maximum when the angle of scattering is $50^{o}$

So For $\phi =50^0$ we get $\theta+50^{o}+\theta=180^{o}$

we get $\theta = 65^{o}$

Co-relating Davisson Germer experiment and de Broglie relation-

According to de Broglie,

$\lambda _{e }= \frac{12.27}{\sqrt{V}}A^{\circ}$

and using V = 54 Volt we get $\lambda _e= 0.167 \ nm$

From Bragg’s formula we have $2d\sin \Theta = n\lambda$

The Lattice Spacing in Ni Crystal is given as d=0.092 nm.

And using $n=1 \ , \phi =50^0 \ and \ V=50 \ Volt$

we get $\lambda_e = 0.165 \ nm$

Therefore the experimental results are in a close agreement with the theoretical values got from the de Broglie equation.

Thus Davisson and Germer Experiment verify the de Broglie equation.

Frank Hertz Experiment-

This experiment is the first experimental verification of the existence of discrete energy states in atoms.

For this experiment, the graph of Collected current Vs Accelerating Voltage is given below

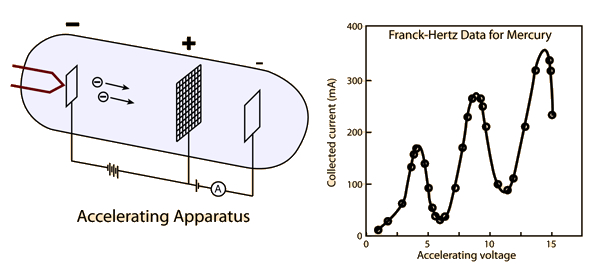
Frank and Hertz had proposed that the 4.9 V characteristic of their experiments was due to the ionization of mercury atoms by collisions with the flying electrons emitted at the cathode.