Physical Pendulum - Practice Questions & MCQ

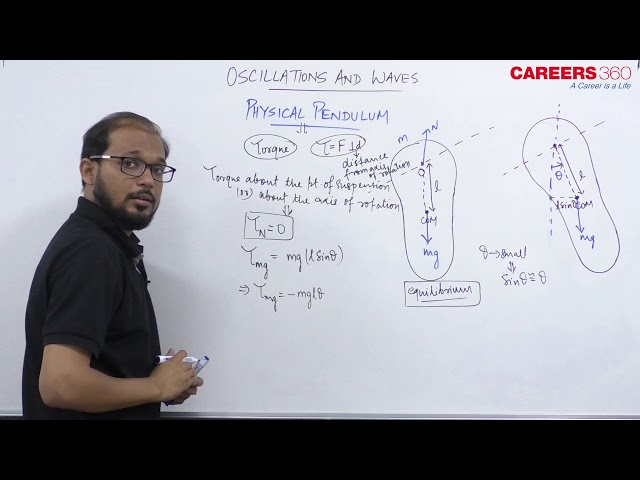
Physical pendulum- Any rigid body suspended from fixed support and can oscillate about that support then it is called a physical pendulum. e.g. A circular ring suspended on a nail in a wall etc.

The body is in equilibrium, as shown in the above fig-1 and it is pivoted about point O.

Now the body is displaced through a small angle  as shown in the fig-2.

Let the distance between the point of suspension and centre of mass of the body=OC=1

Then torque on the body about O is given by $\tau=m g l \sin \theta$
Now if I=moment of inertia of the body about O , Then $\tau=I \alpha \ldots$
From the equation (1) and (2) we get

$
\tau=I \alpha=I \frac{d \theta^2}{d t}=-m g l \sin \theta
$

Since $\theta$ is very small so $I \frac{d \theta^2}{d t}=-m g l \theta$
Comparing with the equation $\frac{d \theta^2}{d t}=-\omega^2 \theta$ we get

$
\omega=\sqrt{\frac{m g l}{I}} \Rightarrow T=2 \pi \sqrt{\frac{I}{m g l}}
$

Note-
Time peried, $T=2 \pi \sqrt{\frac{I}{m g l}} ; \quad I=I_{\mathrm{CM}}+m l^2$
Where $I_{C M}$ is a moment of inertia relative to the axis which passes from the centre of mass and parallel to the axis of oscillation?
$T=2 \pi \sqrt{\frac{I_{\mathrm{CM}}+\mathrm{m} l^2}{m g l}}$, where $\mathrm{I}_{\mathrm{CM}}=\mathrm{mk}^2$
$k$ is gyration radius (about an axis passing from centre of mass)

$
\begin{aligned}
T & =2 \pi \sqrt{\frac{m k^2+m l^2}{m g l}} \\
& =2 \pi \sqrt{\frac{k^2+l^2}{g l}}=2 \pi \sqrt{\frac{l_{\mathrm{eq}}}{g}}
\end{aligned}
$
 

$L_{\mathrm{eg}}=\frac{k^2}{l}+l=$ cquivalent length of simple pendulum

So the graph of the Time period (T) Vs length of a simple pendulum () is shown below

$T$ is minimam when $l=k$

$
\Rightarrow T_{\min }=2 \pi \sqrt{\frac{2 k}{g}}
$