To Find The Focal Length Of A Concave Lens Using Convex Lens - Practice Questions & MCQ

Aim-
To find the focal length of a concave lens using a convex lens.

Apparatus-
An optical bench with four upright (two fixed uprights in middle, two outer uprights with lateral movement), a convex lens (less focal length), a concave lens (more focal length), two lens holders, two optical needles (one thin, one thick), a knitting needle and a half
metre scale.

Theory-

From lens formula,
we have, $f=\frac{u v}{u-v}$
where $f=$ focal length of concave lens $L_2$
$\mathrm{u}=$ distance of I from the optical centre of lens $L_2$
$v=$ distance of I from the optical centre of lens $L_2$
(Note. According to sign convention, u and v have positive values (being measured in the direction of incident light). Since $v>u$, $u$-v is negative. Hence $f$ comes negative.)

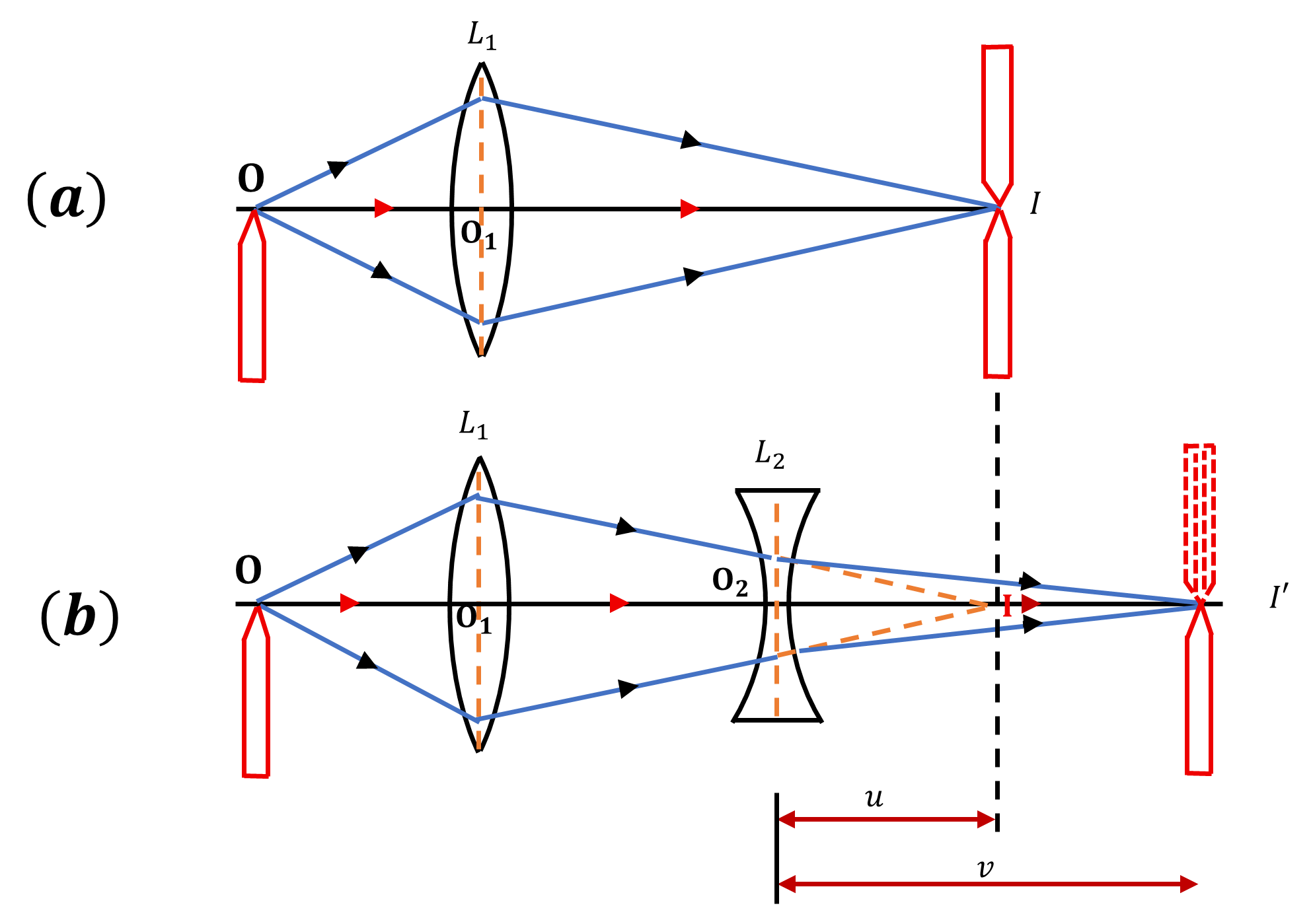
Experiment arrangement and ray diagram-
An object needle 0 is placed on one side of a convex lens $L_1$ and its real inverted image $I$ is located (by image needle) on the other side as shown in the ray diagram.
The concave lens $L_2$ is placed between convex lens $L_1$ and image needle $I$.
The concave lens diverges the rays and the image is now formed at I' as shown in the ray diagram.
For concave lens, $I$ is the virtual object and $I^{\prime}$ is the real image. Hence, $O_2 I=u$ and $O_2 I^{\prime}=v$. Focal length can be calculated, using lens formula

$
\frac{1}{f}=\frac{1}{v}-\frac{1}{u}
$

Procedure: 

To determine the rough focal length of the convex lens
1. Mount the convex lens in the lens holder.
2. Go out in the open and face the lens towards a distant tree or building.
3. Obtain the image of the tree or the building on a white painted wall (screen) and move the lens forwards and backwards to get a sharp image on the wall.
4. Measure the distance between the lens and the wall (screen). This will be equal to the rough focal length of the mirror.

To set the convex lens
5.  Set the object needle
6.  Set the image needle at I
7.   Set the concave lens.
8. Clamp the holder with concave lens on fixed upright on the I side of the convex lens.
9. Fix this upright at some distance away from the convex lens.
10. Set the concave lens surface in the same manner as convex lens surface with principal axes of the lensescoinciding.

11. Then set the image needle at I'

12. Get more and more observations from the experiment and on the basis of observations find out the focal length of the given concave lens.

Calculations-

1. Find the difference of positions of $L_2$ and I
2. Find the difference of positions of $L_2$ and $I^{\prime}$
3. Apply index correction and write corrected value of $u$ and $v$
4. Calculate $f=\frac{u v}{u-v}$
5. Take the mean of different values of as recorded values of $f$

Mean $f=\frac{f_1+f_2+f_3}{3}=\ldots \ldots \mathrm{cm}$.
Result-
The focal length of the given concave lens $=\ldots \ldots \mathrm{cm}$

Precautions-

1. The focal length of the convex lens should be less than the focal length of the concave lens so that the combination is convex.

 2. The lenses must be clean.