To Determine Angle Of Minimum Deviation For A Given Prism By Plotting A Graph Between Angle Of Incidence And The Angle Of Deviation. - Practice Questions & MCQ

Aim-
To determine angle of minimum deviation for a given prism by plotting a graph between angle of incidence
and the angle of deviation.

Apparatus-
Drawing board, a white sheet of paper, prism, drawing pins, pencil, half-metre scale, office pins, graph paper
and a protractor.

Theory-
The refractive index in n of the material of the prism is given by

$$
n=\frac{\sin \left(\frac{A+D_m}{2}\right)}{\sin \left(\frac{A}{2}\right)}
$$

where, $\mathrm{D}_{\mathrm{m}}$ angle of minimum deviation and A angle of the prism.

Diagram-

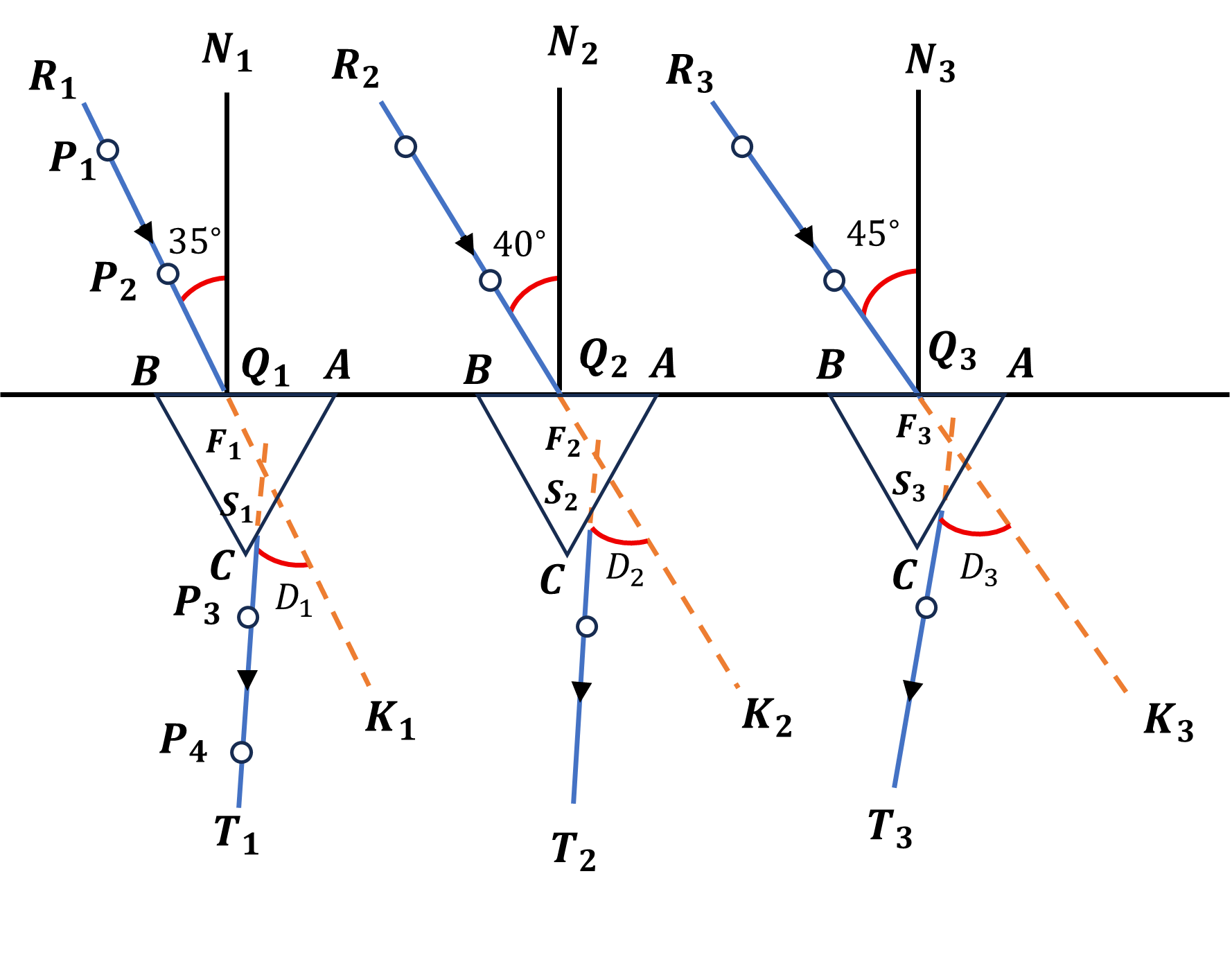
Procedure-

1. Fix a white sheet of paper on the drawing board with the help of drawing pins or tape.
2. Draw a straight line XX' parallel to the length of the paper nearly in the middle of the paper.

3. Mark points $\mathrm{Q}_1, \mathrm{Q}_2, \mathrm{Q}_3, \cdots$ on the straight line XX ' at suitable distances of about 5 cm .
4. Draw normals $N_1 Q_1, N_2 Q_2, N_3 Q_3, \cdots$ on points $Q_1, Q_2, Q_3, \ldots$ as shown in diagram.
5. Draw straight lines $R_1 \mathrm{Q}_1, \mathrm{R}_2 \mathrm{Q}_2, \mathrm{R}_3 \mathrm{Q}_3, \ldots$ making angles of $35^{\circ}, 40^{\circ}, \ldots 60^{\circ}$ (write value of the angles on the paper) respectively with the normals.
6. Mark one corner of the prism as $A$ and take it as the edge of the prism for all the observations.
7. Put it prism with its refracting face $A B$ in the line $X X^{\prime}$ and point $Q_1$ in the middle of $A B$.
8. Mark the boundary of the prism.
9. Fix two or more office pin $\mathrm{P}_1$ and $\mathrm{P}_2$ vertically on the line $\mathrm{R}_1 \mathrm{Q}_1 \mathrm{P}_1$ and $\mathrm{P}_2$ vertically on the line $\mathrm{R}_1 \mathrm{Q}_{1 \text { The distance between the pins should }}$ be 10 mm or more.
10. Look the images of point $\mathrm{P}_1$ and $\mathrm{P}_2$ through face AC .
11. Close your left eye and bring open right eye in line with the two images.
12. Fix two office pins $P_3$ and $P_4$ vertically, and 10 cm apart such that the open right eye sees pins $P_4$ and $P_3$ and images of $P_2$ and $P_1$ in one straight line.
13. Remove pins $P_3$ and $P_4$ and encircle their pricks on the paper.
14. Repeat steps 7 to 13 with points $Q_2, Q_3, \ldots$ for $i=40^{\circ}, \ldots, 60^{\circ}$.

To measure D in different cases
15. Draw straight lines through points $P_3$ and $P_4$ \{pin pricks) to obtain emergent rays $\mathrm{S}_1 \mathrm{~T}_1, \mathrm{~S}_2 \mathrm{~T}_2, \mathrm{~S}_3 \mathrm{~T}_3 \ldots \ldots$
16. Produce $T_1 \mathrm{~S}_1, \mathrm{~T}_2 \mathrm{~S}_2, \mathrm{~T}_3 \mathrm{~S}_3, \ldots$ inward in the boundary of the prism to meet produced incident rays $\mathrm{R}_1 \mathrm{Q}_1$,
$\mathrm{R}_2 \mathrm{Q}_2, \mathrm{R}_3 \mathrm{Q}_3, \cdots$ at points $\mathrm{F}_1, \mathrm{~F}_2, \mathrm{~F}_3, \cdots$
17. Measure angles $\mathrm{K}_1 \mathrm{~F}_1 \mathrm{~S}_1, \mathrm{~K}_2 \mathrm{~F}_2 \mathrm{~S}_2, \mathrm{~K}_3 \mathrm{~F}_3 S_3, \ldots \ldots$.

These give angle of deviation $\mathrm{D}_1, \mathrm{D}_2, \mathrm{D}_3, \ldots$
18. Write values of these angles on the paper.

To measure A
19. Measure angle BAC in the boundary of the prism. This gives angle A.
20. Record your observations.

Calculation:

Plot a graph between angle of incidence $\angle i$ and angle of deviation $\angle D$ by taking $\angle i$ along X -axis and $\angle D$ Y -axis. From this graph, find the value of a single minimum deviation $\mathrm{D}_{\mathrm{m}}$ corresponding to the lowest point of the graph.

Let the value of angle of minimum deviation, $D_m=\ldots$.

Then

$$
n=\frac{\sin \frac{A+D_m}{2}}{\sin A / 2}
$$

Result
1. i-D graph indicates that as the angle of incidence (i) increases, the angle of deviation (D) first decreases, attains a minimum value $\left(D_m\right)$ and then starts increasing for further increase in angle of incidence.
2. Angle of minimum deviation, $D_m=\ldots \ldots$.
3. Refractive index of the material of the prism, $n=\ldots \ldots$.